Sine-Gordon Solitons and Breathers in Rod-like Magnetic Liquid Crystals under External Magnetic Field?
Yan Li(李妍),Xiao-Bo Lu(魯小波),and Chun-Feng Hou(侯春風(fēng)),?
1Department of Physics,Harbin Institute of Technology,Harbin 150001,China
2Department of Physics Science and Technology,Heilongjiang University,Harbin 150080,China
AbstractTo study the nonlinear phenomena in rod-like magnetic liquid crystals(RMLCs),this paper establishes the dynamic model of molecular motion when giving a twisting disturbance to the molecules under external magnetic field.We find the twist of the molecules under magnetic field can be propagated in the form of a traveling wave.The dynamic equation of the molecular twisting we derived satisfies the form of Sine-Gordon equation.We obtain two solutions of the Sine-Gordon equation by theoretical calculation:the kink and anti-kink solitons and breathers.The characteristics of those solitons and breathers are discussed.
Key words:rod-like magnetic liquid crystals,Sine-Gordon equation,kink and anti-kink solitons,breathers
1 Introduction
Liquid crystal is a kind of important optical material,which is widely used in optoelectronic display devices with characteristics of solid and liquid materials.There are many optical nonlinear phenomena in liquid crystals,[1?2]including optical solitons.[3?8]As early as 1968,the solitons in nematic liquid crystals was proved theoretically.Then many researches have been carried out on the solitons in nematic liquid crystals,[9?15]as well as breathers in the nematics.[16?17]Magnetically induced solitary waves were found to evolve in a nematic liquid crystal by Helfrich.[18]Further the novel nonlinear dissipative dynamic patterns was reported by Migler and Meyer,and several types of soliton structures in the nematic liquid crystal systems under the in fluence of a continuously rotating magnetic field were observed.[19]Since 1987,Raikher et al.studied the in fluence of an external magnetic field on the state of magnetization and separation of the magnetic phase in a nematic doped with needlelike ferrite particles,[20]the magnetic properties were combined with the nematic liquid crystals as a special functional materials in order to obtain a new organic magnetic material.More and more people combine molecular magnetic materials with liquid crystals to make liquid crystal materials multifunctional.By combining magnetic perssad on nematic liquid crystal molecules and giving magnetic properties to nematic liquid crystal materials with fluidity,it is possible for nematic liquid crystal molecules to be arranged in order under external magnetic field,which can make nematic liquid crystal used more widely.[21?25]In this paper,we investigate the twist of the RMLC molecules.We construct the dynamic model of the director under the magnetic field,then we deduce the dynamic equation of the molecules by referring to the Frenkel-Kontorova model[26]and find that it satisfies the Sine-Gordon equation.We solve the equation and get the solution of solitons and breathers.
2 The Twisting Dynamic Equation of RMLC Molecules under Magnetic Field
RMLC materials have obvious magnetic properties.We consider the twist of the RMLC molecules with inherent magnetic moment in the external magnetic field.Here,we will use the method similar to the one dimensional single atom chain model[27]and consider the in fluence of the adjacent molecules to describe the one-dimensional twist of RMLC molecules under external magnetic field.
Assuming the magnetic moment of the i-th RMLC molecule is,the potential energy of the entire system under the magnetic field is given by

Now we discuss the twisting motion of RMLC molecules propagating along the x axis.The molecular motion is described by θi= θi(x,t),where θiis the angle of the i-th molecule with the direction of external magnetic field after its twisting.When there is only the external magnetic field and the RMLCs are contained in a cell,the twist effect of RMLC molecules is more obvious than their collective flow,so the impact of the molecular flow kinetic energy on the whole system can be ignored. Because the molecules twisted,we believe that the molecule twists around the axis,which is perpendicular to the direction of its center.So the overall rotational kinetic energy is given by

where Iiis the moment of inertia of the i-th RMLC molecule,when a single RMLC molecule rotates around the center of its long axis,its moment of inertia is Ii=,where miis the mass of the i-th molecule.As the morphological difference between the same kind of liquid crystal molecules is not much,the quantities are assumed to be equal as mi=m,Li=L,Ii=I.Because of liquid viscosity,the interaction between molecules can be assumed to be elastic potential energy,which is related to the relative position of the interacting molecules.The change of the relative position of RMLC molecules is only the change of the deflection angle.Taking only in fluence of the adjacent molecules,the potential energy takes the form

where K22represents the frank twist deformation elastic constants,which is related to the chemical composition of the RMLC molecules.The Hamiltonian of this system is given by

From Eq.(4),we have

According to the Hamilton canonical equation=??H/?θ,we get

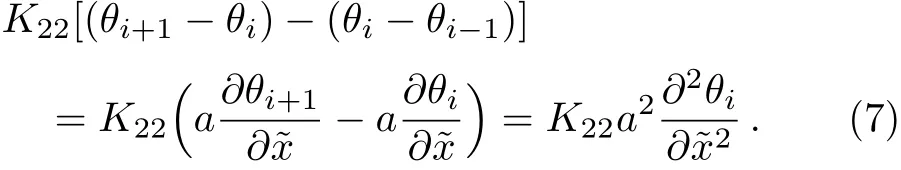
Omit the subscript i,from Eqs.(6)and(7),we have
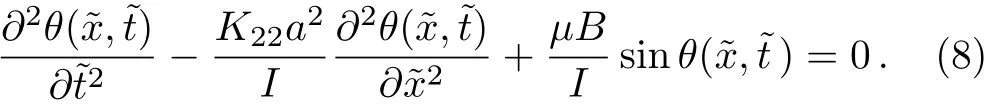
The dynamic equation of the RMLC molecules in the liquid crystal cell we obtained is similar to Sine-Gordon equation.As is known,the normal Sine-Gordon equation is one of the nonlinear equations with solitary solutions,so the solitary phenomena is possible to appear in the RMLC molecules under external magnetic field.To make it easier to study,we can make the space-time coordinate transformation to Eq.(8).Letwhereandare space-time coordinate transformation constants.In order to make the equation further reduced,letwe get

where t and x are dimensionless time and space coordinate respectively,u(x,t)is the deflection angle of the RMLC molecules under the external magnetic field at the moment t and in the position x,K22is the frank twist deformation elastic constant,which is generally 10?5N/m and we choose the typical value 1.3× 10?5N/m here.The distance a between the adjacent RMLC molecules is generally nanometer.I=/12 is the moment of inertia of a single RMLC molecule,where m0is the mass of a single RMLC molecule,which is related to the chemical composition of the molecule and L0is the length of a single RMLC molecule,which is generally nanometer.The magnetic moment per unit volume of the RMLC molecule should be 10?6A/cm and we use 5.3×10?6A/cm here.[28]The applied magnetic field B can be given about several hundred mT.In order to simplify the calculation,the coordinates of time and space are dimensionless.The realistic physical values of time can be selected several millisecond according to the molecular response time and the space coordinate can be selected nanometer as the distance between the adjacent RMLC molecules is nanometer.
3 Solutions of Kink and Anti-Kink Solitons and Breathers
To solve the Sine-Gordon equation with a trial solution of the traveling wave,[29]we set ξ=x ? vt,u=u(ξ),substituting them into Eq.(9)yields

where v is a constant,which denotes the propagating velocity of the traveling wave.Equation(10)can be solved by using Jacobi elliptic function expansion method,when,it can be reduced to
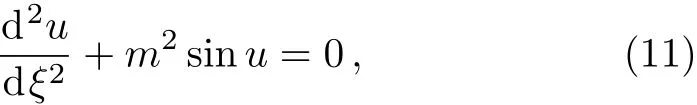

Integrating Eq.(12),we get

where H0is a constant of integration,which denotes the initial state of the entire system,and H0≥0 as we know from its expression.As 1?cosu=2sin2(u/2),Eq.(13)can be reduced to

We can find a constant k such that H0=2m2k2,of course,we can see that k should satisfy the conditions k2<1 through a simple calculation.Equation(14)can be given

Introducing the intermediate variable φ,which satisfies the condition sin(u/2)=ksinφ,differentiate both sides of the equation yields
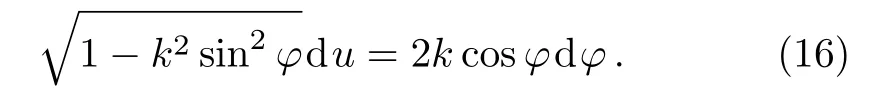
We derive

Substituting Eq.(17)into Eq.(15)and reducing it yields
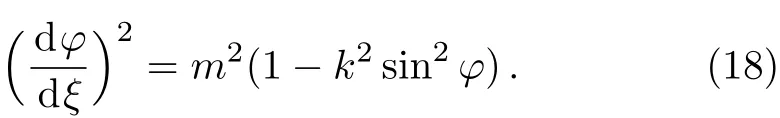
As k2<1,extracting the root of Eq.(18)we have

Integrating Eq.(19),we obtain
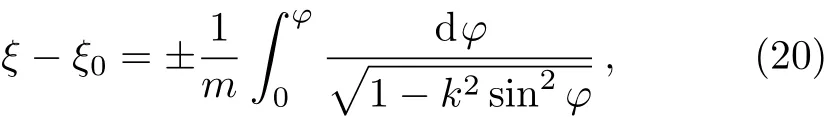
where ξ0is a constant of integration.The right side of Eq.(20)is the integral inversion of the Jacobian elliptic function sn(u,k),which satisfies sinφ = ±sn[m(ξ?ξ0),k].
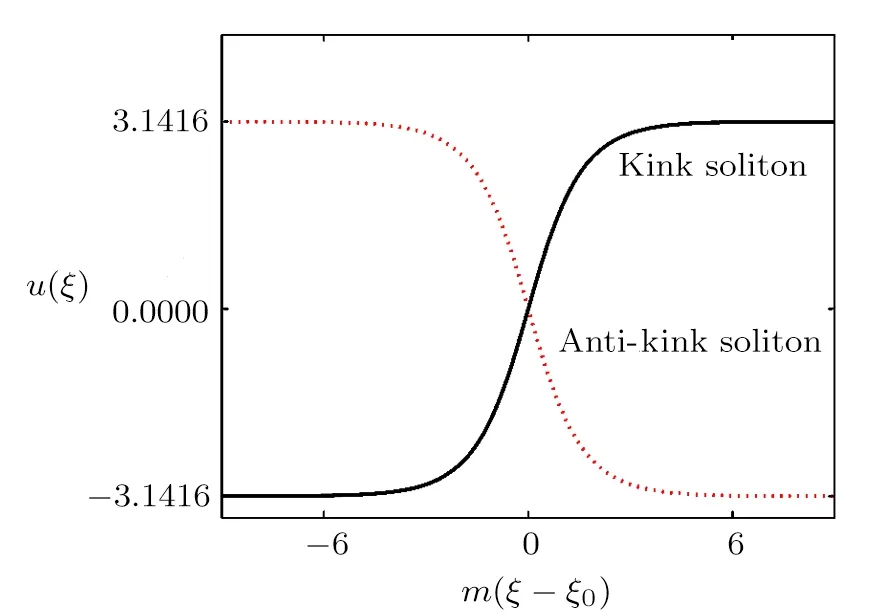
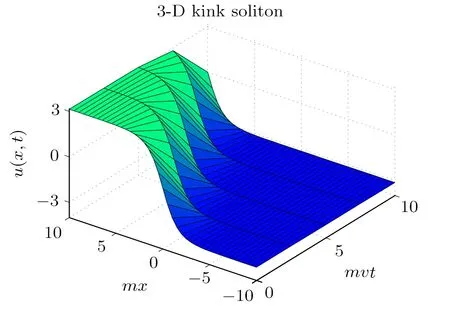
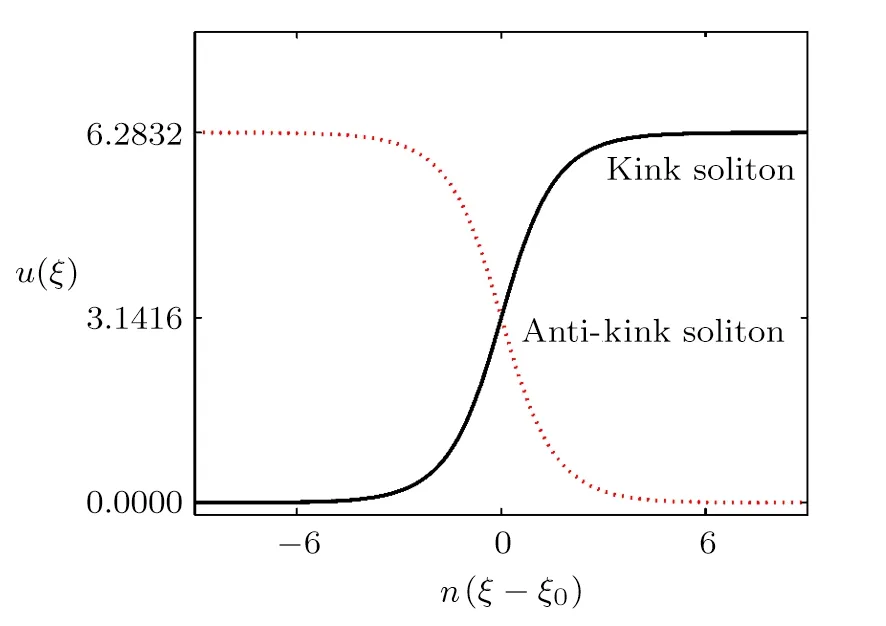
When 0 and?π The result is a linear wave solution,which corresponds to the initial state of the system H0→0.It illustrates that the initial perturbation is so little that results in a slight oscillation,which has no practical and physical meaning.So the linear waves generated by the twist of RMLC molecules can be neglected. Another way to obtain the analytical solution of the equation by Jacobian elliptic function boundary condition is k2→1,integrating Eq.(19),we get Considering the definition of hyperbolic tangent function,we have So we derive the solution Thereby we further obtain The results obtained above are a couple of unbound double soliton solutions,also called kink soliton and anti-kink soliton,which correspond to the positive and negative sign of Eq.(26).As we see in Figs.1–3,the pro file of the two waves are unchanged when they are propagating,which is the characteristics of solitary waves.We have (i)Kink soliton:when ξ→ +∞,then u→ π;when ξ→?∞,then u→?π. (ii)Anti-kink soliton:when ξ→ +∞,then u→ ?π,when ξ→ ?∞,then u→ π. The molecular twist direction described by kink soliton and anti-kink soliton is opposite to each other. Fig.1 Schematic diagram of a couple kink solitons. Fig.2 Time evolution of kink solitons. Fig.3 Time evolution of anti-kink solitons. In the case of v2<,using Jacobi elliptic function expansion method as well,we obtain another solution of kink and anti-kink soliton It is shown in Fig.4. (i)Kink soliton:when ξ→ +∞,then u → 2π;when ξ→?∞,then u→0. (ii)Anti-kink soliton:when ξ→ +∞,then u→ 0;when ξ→ ?∞,then u → 2π. Fig.4 Schematic diagram of a couple kink solitons when Now we try to get the bound solution of the Sine-Gordon equation.We transform Eq.(9)by using t1=f0t,x1=(f0/v0)x,we have Let the trial solution be where X(x1)is the function of x1,T(t1)is the function of t1.We have As is known to all Substituting Eqa.(31),(32),and(33)into Eq.(28),we have The newspapers came out next morning with a border of hearts round it, and the princess s monogram26 on it, and inside you could read that every good-looking young man might come into the palace and speak to the princess, and whoever should speak loud enough to be heard would be well fed and looked after, and the one who spoke25 best should become the princess s husband Di ff erentiating Eq.(34)for x1and t1respectively yields Add Eqs.(35)and(36)together,we obtain where 4α is a constant,thus Integrating the two equations above,at the same time,Eq.(34)should be satisfied,we get where β is an integration constant,given by the initial condition.For Eqs.(39)and(40),different elliptic equations are obtained by taking different values of α and β.When 0< β<1,α<0,the equations above satisfy the fourth kind of elliptic equation.When α = ?1,integrating Eqs.(39)and(40),we have Substituting Eqs.(41)and(42)into the trial solution,the deflection angle of the RMLC molecules can be obtained First we take into account the effect of the parameter β on the results.Considering the RMLC molecule on a certain point(x,t),we find that u(x,t)and W varies with β as is shown in Fig.5.It can be seen from the trend of the curve in Fig.5 that u(x,t)and W vary linearly with β when β <0.6.In this range,the value of β does not essentially affect our study results.We choose β=0.5 here. Fig.5 The amplitude of the liquid crystal molecular deflection u(x,t)and the half peak width W varies with β. The spatiotemporal distribution of the results is shown in Fig.6.u(x,t)distributes on both sides of x=0 symmetrically and is bound to the x axis,which does not propagate in space as time goes on.Over time,all the points on the x axis are periodically transformed,and the half-peak width shrinks and expands periodically.Selecting different time sampling points in one cycle,the shape of u(x,t)is shown in Fig.7,which we call it breathers. Fig.6 The graphic model of breathers in RMLCS under magnetic field when β=0.5. The frequency of breathers is,which expresses the speed of the periodic deflection of RMLC molecules near the equilibrium position. Fig.7 The morphological diagram of breathers changing with time,from top to bottom is the form of breathers at different times,respectively. The RMLC molecules under magnetic field twist around its transverse axis by the external perturbation.The twisting molecule drives the adjacent molecules twist.Our study shows that the twisting process of RMLC molecules satisfies the Sine-Gordon equation and the twisting motion of the molecules can be propagated in the form of kink and anti-kink Sine-Gordon solitons.When v2>,the deflection angle of the RMLC molecules distributes in the interval(?π,π).We can see from its propagation diagram that the shape and the speed of the distribution do not change during the time.The physical meaning of the double kink solitons is that the distribution of the deflection angle is opposite to each other.It means that molecular twist direction described by the kink soliton and the anti-kink soliton is opposite to each other,and the sign denotes two different directions.When v2<,the contours of solitary waves does not change,but the overall shape move up+π.That is the deflection angle distributes change from(?π,π)to(0,2π).It indicates that the whole shape of the wave rotate π to the axis along the propagation direction compared to v2>.Due to rotational symmetry,this condition is not substantially different from the previous solitary wave pattern. Another solution of Sine-Gordon equation is breather.The deflection angles of RMLC molecules are different at different coordinates,but they all change periodically.For the RMLC molecules in all the spatial directions in the liquid crystal cell,the maximum deflection angle of each point changes gradually with the coordinate,the deflection angle at the maximum deflection can be reached to 2π,the changing trend is the outline of the breathers,and the frequency of the breathers is the one of the oscillation of the RMLC molecules at all points in the liquid crystal cell.The distribution and the frequency of the breathers are related to the RMLC itself and the external magnetic field. The kink and anti-kink solitons are a couple of solitary waves,which describe the opposite molecular twist direction respectively in RMLC molecules. While the breathers are the periodic deflection of a single liquid crystal molecule in its “equilibrium position”,which is not walking waves,but like standing waves.We predict that the solitons and breathers can be observed in experiment under suitable conditions and we will take the experiment in the future.




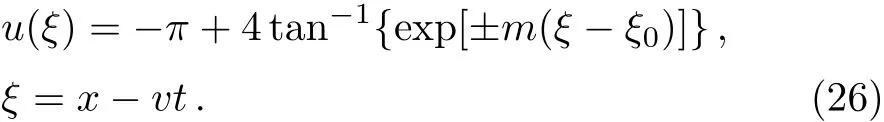








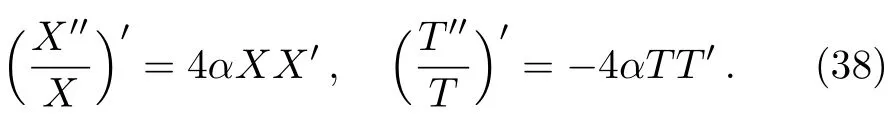

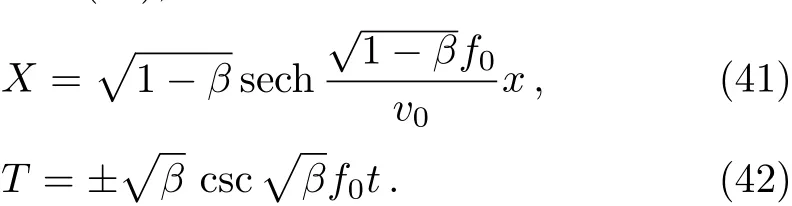

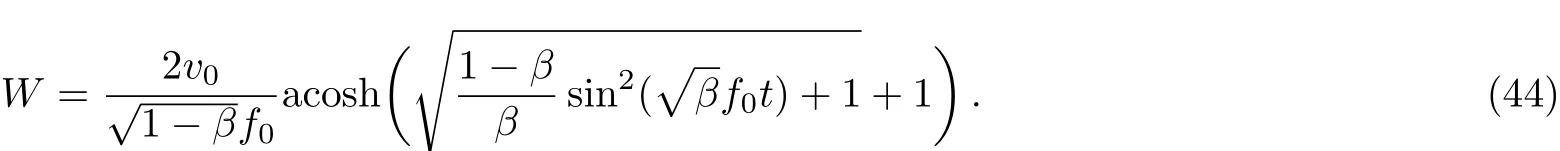



4 Conclusion
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
