K2 for a kind of special finite group rings*
ZHANG Yakun, TANG Guoping
(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract Let G be a non-trivial group of order less than 6, p a prime dividing the order of G, we obtain the structure of K2(G/pkG) for k≥2.
Keywords K2-group; Dennis-Stein symbols; group rings
LetGbe a finite abelianp-group, and Γ the maximal-order ofGinG. By Proposition 2.2 in Ref.[1], Γ is the integral closure ofGinG, and |G|Γ?G?Γ. When 1<|G|<6, we find that calculation ofK2(G/pkG)(k≥2) is equivalent to calculation ofK2of a quotient ring of Γ. Our method relies on the explicit structures ofK2(G) andK2(Γ), which are listed in Table 1. A brief introduction to the explicit structures ofK2(G) andK2(Γ) can be found in Ref.[2].
For simplicity, for any positive integerk≥2, we define
Table 1 Structures of K2(G) and K2(Γ)

Table 1 Structures of K2(G) and K2(Γ)
GΓK2(ZZG)K2(Γ)C2ZZ2(C2)2(C2)2C3ZZ⊕ZZ[ζ3]C2C2C4ZZ2⊕ZZ[i](C2)2(C2)2C5ZZ⊕ZZ[ζ5]C2C2(C2)2ZZ4(C2)6(C2)4
We summarize our results in Table 2.
1 Preliminaries
Lemma1.1Let O be a totally imaginary

Table 2 Main results (k≥2)
Dedekind domain of arithmetic type with field of function. Letps=|μp()|, whereμp() is thep-th power roots unity in the field. Then for any integerm>1,SK1(O,mO) is a cyclic subgroup ofμ() of orderl, where
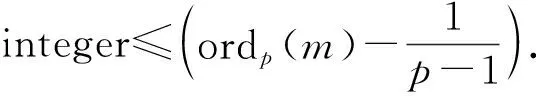
ProofThis follows directly form Corollary 4.3 in Ref.[3].
Lemma1.2Let 1<|Cpr|<6. Then for any integerk≥r≥1.
K2([ζpi]/(pk)).
ProofLetR=Cpr,I=pkΓ such thatk≥r. By Proposition 2.2.(b) in Ref.[1], we haveI?R. Then the Cartesian square
gives rise to a nature commuative diagram with exact rows




By Corrollary 1.6 in Ref.[4],K2(R) maps ontoK2(Γ). Hence, it is indicated in Table 1 thatφ2is an isomorphism induced by inclusion. According to Theorem 1.3 in Ref.[1],φ1is a surjection andφ4is an isomorphism. Since both ofSK1(R) andSK1(Γ) are trivial,φ5is an isomorphism. A diagram chasing shows thatφ3is an isomorphism. Hence,
K2(Cpr/pkГ)≌K2(Γ/pkΓ).
According to Corollary 2.10 in Ref.[5],Cpris isomorphic to a direct sum of cyclotomic field
(ζpi).
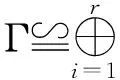
□
2 Main results
It is well known thatK2(/(2k))=C2(k≥2). If[ζpi] is totally imaginary, by Lemma 3.4, Theorem 3.8 and 5.1 in Ref.[6], and Corollary 4.3 in Ref.[3],
K2([ζpi]/(pk))≌SK1([ζpi],(pk)).
Fork≥2, using Lemma 1.1 and Lemma 1.2, we deduce thatK2(C2/2kΓ)=(C2)2,K2(C3/3kΓ)=C3,K2(C5/5kΓ)=C5,K2(C4/2kΓ)=(C2)2?C4(k≥3), andK2(C4/4Γ)=(C2)3.
Note that, for any integers≥r,pr+sΓ?psCpr?psΓ. Hence, according to Proposition 1.1 in Ref.[7],K2(Cpr/pr+sΓ) maps ontoK2(Cpr/psCpr) andK2(Cpr/psCpr) maps ontoK2(Cpr/psΓ). Therefore, we deduce that fork≥2,K2(C2/(2k))=(C2)2,K2(C3/(3k))=C3,K2(C5/(5k))=C5,K2(C4/(2k))=(C2)2?C4(k≥3), andK2(C4/(4))=(C2)3since, by Lemma 4.1.(a) in Ref.[7],K2(C4/(4)) has an exponent of 2.Summarizing, we have proven the theorems as follows.
Theorem2.1K2(C2/(2k))(k≥2) is an elementary abelian 2-group of rank 2.
Theorem2.2For any integerk≥2,
K2(
Theorem2.3For any integerk≥2 andp=3,5,K2(Cp/(pk)) is a cyclic group of orderp.
The method mentioned above is not suitable for the case whenG=(C2)2. However, we have the result as follows.
Theorem2.4Let (C2)2=〈σ〉×〈τ〉 be an elementary abelian 2-group of rank 2. ThenK2((C2)2/(2k))(k≥2) is an elementary abelian 2-group of rank 6 with generators
{-1,-1},{σ,-1},{τ,-1},{σ,τ},
〈σ-1,τ(σ+1)〉 and 〈τ-1,σ(τ+1)〉.
ProofAccording to Theorem 1.10 in Ref.[7],SK1((C2)2,(2k)) is trivial. From the relativeK-theory exact sequence associated to the pair ((C2)2,(2k)),K2((C2)2) maps ontoK2((C2)2/(2k)). We deduce from the result of Ref.[2] thatK2((C2)2/(2k)) is an elementary abelian 2-group of rank at most 6.
Besides, from Proposition 1.1 in Ref.[1],K2((C2)2/(2k)) maps ontoK2(2(C2)2). Obviously, the kernel contains {-1,-1}, {σ,-1}, and {τ,-1}, while by the result on page 272 in Ref.[7], they are nontrivial and linearly independent. Based on Theorem 4 and Example 3 in Ref.[8],K2(2(C2)2) is an elementary abelian 2-group of rank 3 with generators {1+σ+τ,σ},{1+σ+τ,τ}, and {σ,τ}. Therefore, the 2-rank ofK2(2(C2)2) is at least 6.
Hence,K2((C2)2/(2k)) is isomorphic toK2((C2)2). In Ref.[2], the explicit structure ofK2((C2)2) is given. The result follows.
□

