趙 健,楊叢麗,潘維燁

(貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,貴州貴陽(yáng) 550001)

1 引言

設(shè)C表示復(fù)平面,H(C)表示在C上的解析函數(shù)全體,dA表示C上的Lebesgue面積測(cè)度,是由L2(C,e?α|z|2dA(z))中的整函數(shù)所構(gòu)成的空間,0＜α＜∞,即

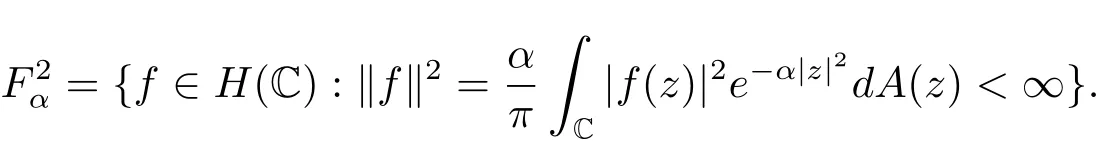
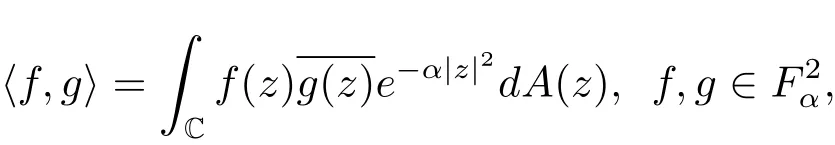
其規(guī)范正交系為

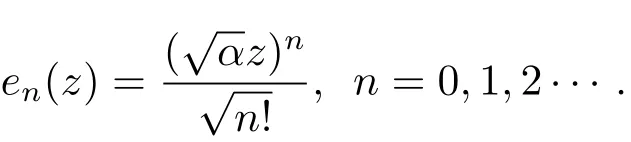
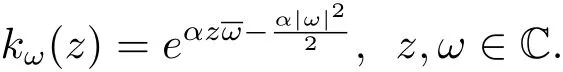
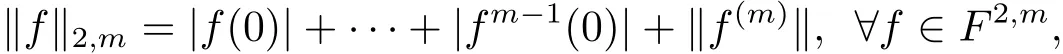
這里‖·‖表示F2的范數(shù).

Cho和Zhu[8]證明了f∈F2,m當(dāng)且僅當(dāng)zmf∈F2.因此,F2,m的范數(shù)也可以表示為

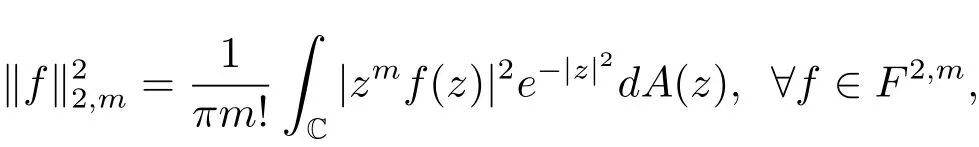
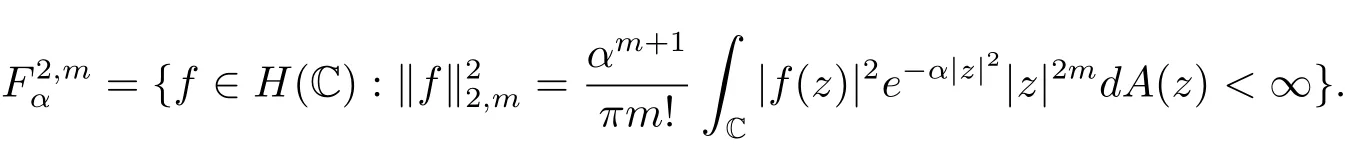
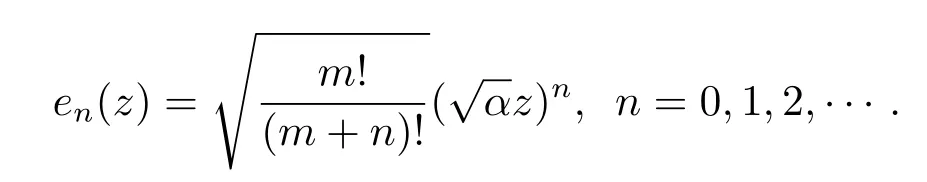
有關(guān)Fock-Sobolev空間的更多研究,可參見文獻(xiàn)[9–14].

設(shè)T∈B(X),X 是Hilbert空間,稱T是X上的Hilbert-Schmidt算子,如果

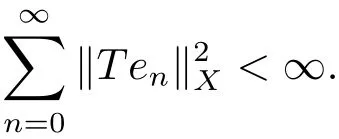
在本文中M表示一個(gè)正常數(shù),每次出現(xiàn)不一定相同.

2 主要結(jié)果及證明

為了證明本文的主要結(jié)果,需要用到下面的一些輔助結(jié)論.

引理2.1設(shè)?是C上的解析自映射,μ∈H(C),0＜α＜∞,則為緊的充分必要條件為有界且對(duì)中任意有界并在C的任意緊子集上一致收斂于0的序列{fn},n∈N+,有

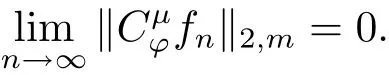
通過使用類似于文獻(xiàn)[21,命題3.11]的方法,可以證明引理2.1.

引理2.2若序列{fn}在中弱收斂于0,則{fn}一致有界且在C的任意緊子集上一致收斂于0.

證由于序列{fn}在中弱收斂于0,則對(duì)任意于是

因此存在與z有關(guān)的常數(shù)Mz＞0,使得|fn(z)|≤Mz,而C是完備的,由一致有界原理可得序列{fn}一致有界,即存在M ＞0,使得設(shè)D是C中的任一緊子集,Kz為的再生核,可將Kz看成是C到上的一個(gè)映射,且對(duì)任意z0∈D,有

顯然,當(dāng)z→z0時(shí),‖Kz?Kz0‖→0,這說明Kz為連續(xù)映射,由于D是緊的,故Kz在D上一致連續(xù).因此對(duì)任意的ε＞0,存在δ＞0,對(duì)任意的z′,z′′∈D,當(dāng)|z?z0|＜δ時(shí),

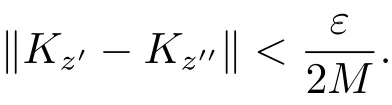
由于 D緊,則 D是完全有界的,于是,對(duì)上述的 δ,存在 z1,z2,···,zq∈ D,使得 D ?由于

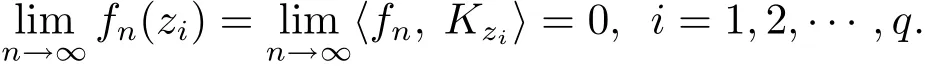
因此對(duì)上述的 ε,存在 Ni＞ 0,i=1,2,···,q,當(dāng)任意 n ＞ Ni時(shí),從而取N=max{N1,N2,···,Nq},對(duì)任意的z∈ D,一定存在zj∈ D,1≤ j≤ q,使得|z?zj|＜ δ,當(dāng)任意的n＞N時(shí),有

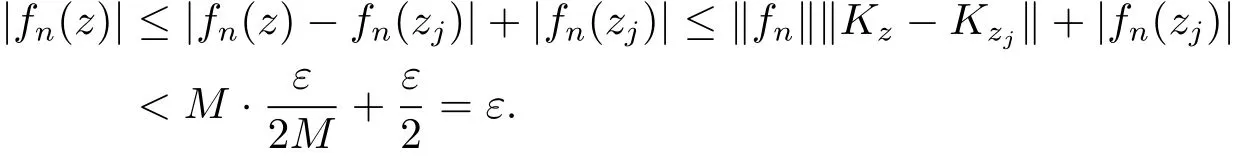
故{fn}在C的任一緊子集上一致收斂于0.

引理2.3設(shè)?是C上的解析自映射,μ∈H(C),0＜α＜∞,則為緊的充分必要條件為有界且對(duì)中任意弱收斂于0的序列{fn},n∈N+,有

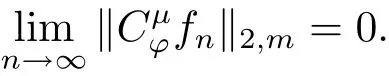
證 由引理2.1和引理2.2即可得證.

引理2.4設(shè)kω為中的正規(guī)化再生核,則當(dāng)|ω|→∞時(shí),kω弱收斂于0.即對(duì)任意的

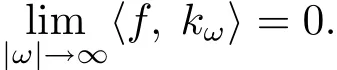
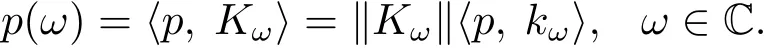
于是

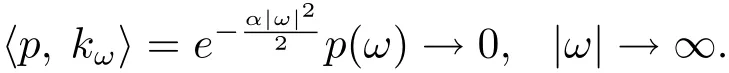
下面的引理是文獻(xiàn)[22,推論2.8]稍作推廣后的結(jié)果,它在本文主要結(jié)果的證明中有著重要作用.當(dāng)α=1時(shí),就是文獻(xiàn)[22]中的結(jié)論.

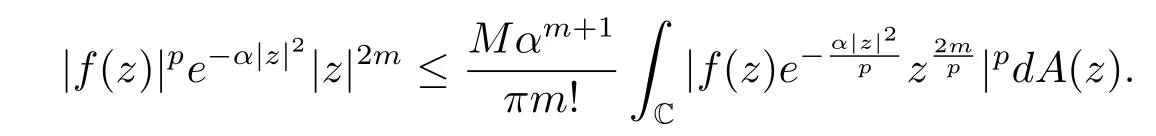
使用類似于文獻(xiàn)[22]的方法可以證明引理2.5.

下面的結(jié)論來自于文獻(xiàn)[23].

引理2.6設(shè)?是C上的解析自映射,μ∈H(C),0＜α＜∞,若

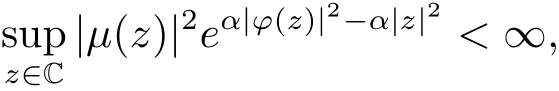
則存在常數(shù)a,b∈C且|a|≤1,使得?(z)=az+b,z∈C.進(jìn)一步,若

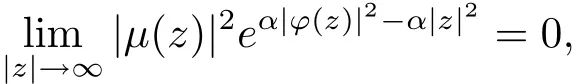
則?(z)=az+b,z∈C且|a|＜1.

嚴(yán)格地說,引理2.6是文獻(xiàn)[23]中結(jié)論稍作推廣后的結(jié)果,當(dāng)α=1時(shí),引理2.6就是文獻(xiàn)[23]中的結(jié)論.實(shí)際上,上述各個(gè)引理中的常數(shù)α在具體的證明中并沒有本質(zhì)作用.

接下來證明本文的主要結(jié)論.

定理2.1設(shè)?是C上的解析自映射,μ∈H(C)且μ≠0,0＜α＜∞,則下列陳述等價(jià):

(ii)

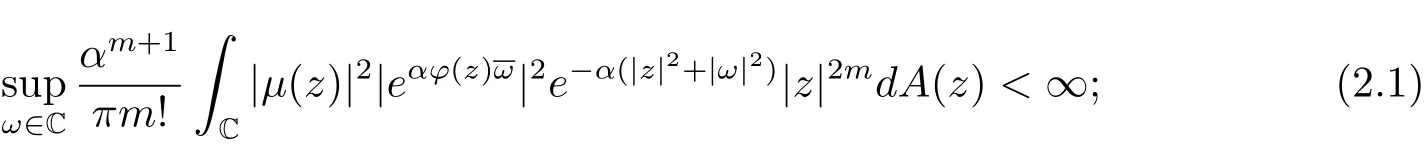
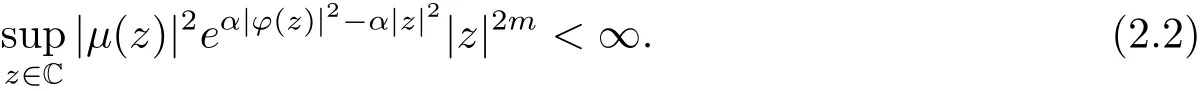
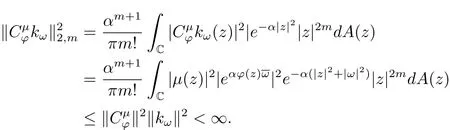
從而

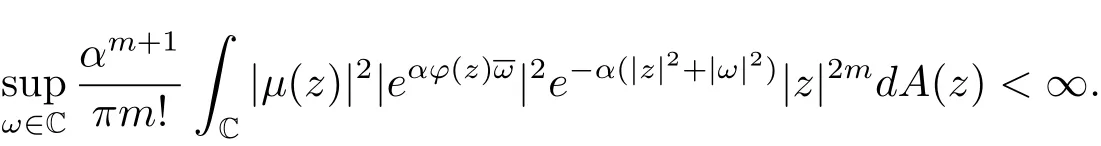
即(2.1)式成立.

(ii)?(iii).若(2.1)式成立,則對(duì)任意ω∈C,

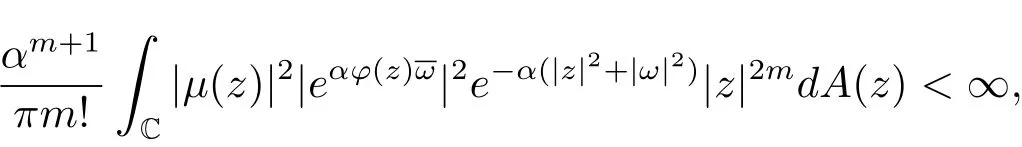
即

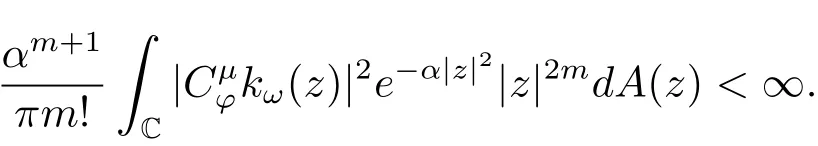
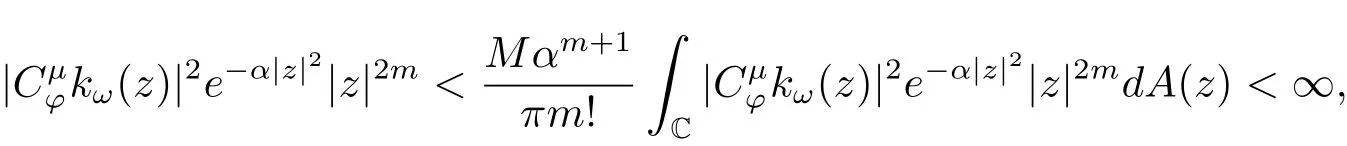
即

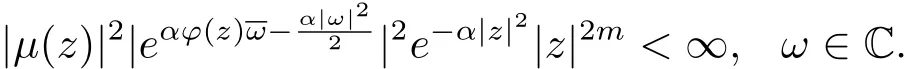
特別地,取ω=?(z),則

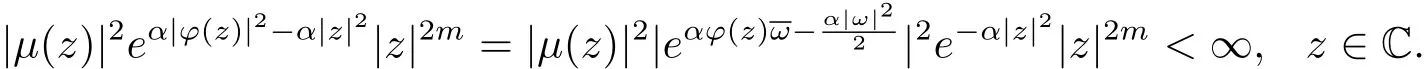
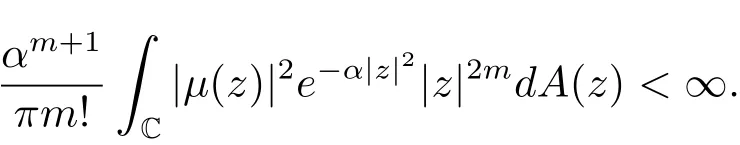
(iii)?(i).若存在常數(shù)a,b∈C,|a|≤ 1,使得?(z)=az+b,z∈C.令ω= ?(z),則當(dāng)0＜|a|≤1時(shí),由(2.2)式,存在M ＞0,使得

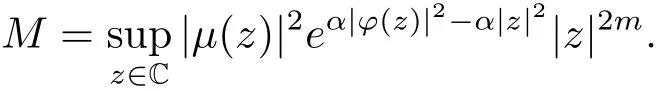
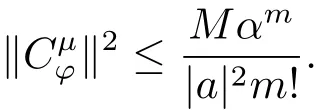
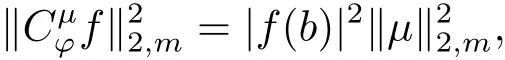
定理2.2設(shè)?是C上的解析自映射,μ∈H(C)且μ≠0,0＜α＜∞,則下列陳述等價(jià):

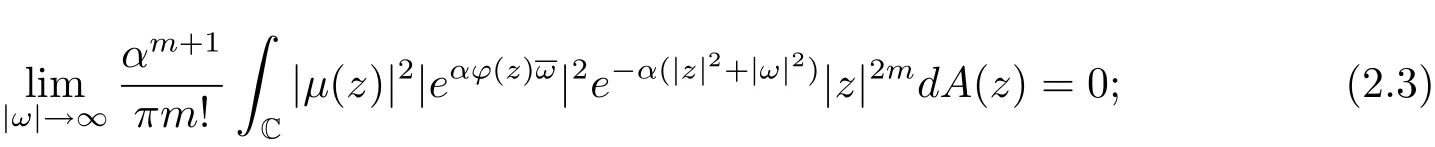
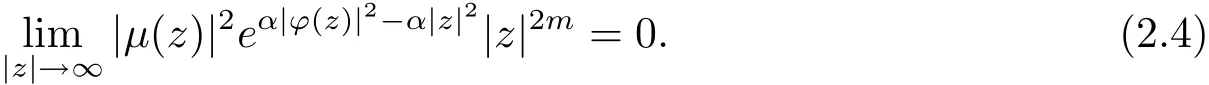
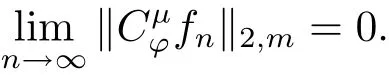
設(shè)kω為中的正規(guī)化再生核,{ωn}為C中任意趨于無窮的點(diǎn)列,由引理2.4,當(dāng)n→∞時(shí),{kωn}弱收斂于0.于是

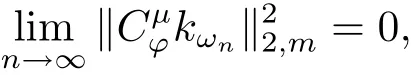
從

而

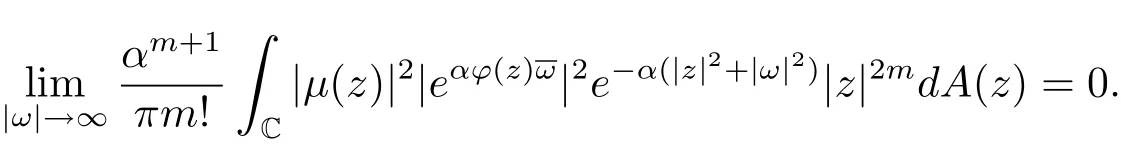
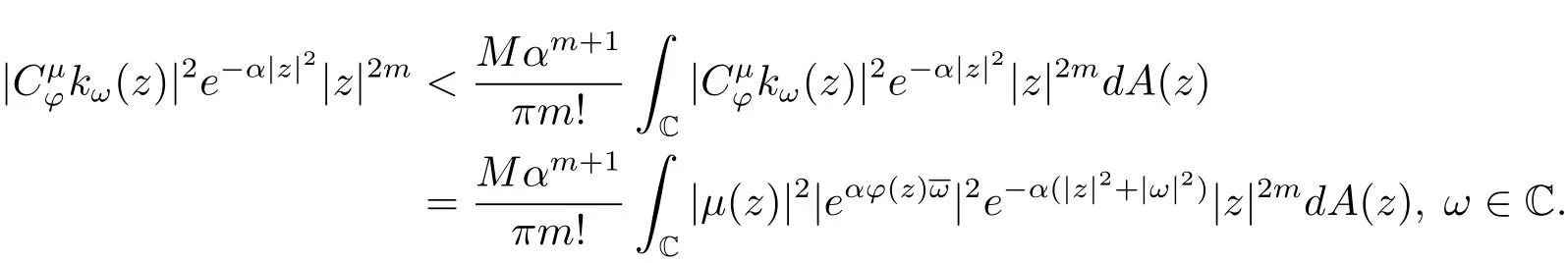
由(2.3)式可得

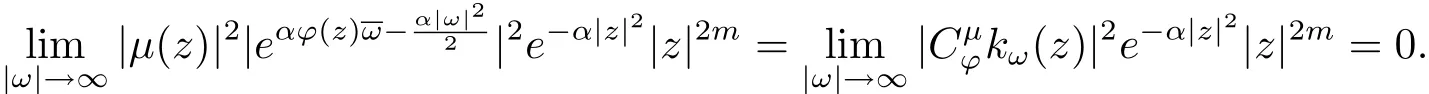
由上式,任意的ε＞0,存在Rε＞0,當(dāng)|ω|＞Rε時(shí),

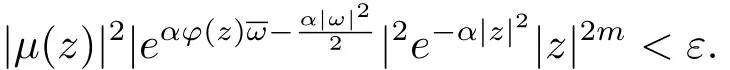
當(dāng)0＜ |a|≤ 1時(shí),令 ω = ?(z),則 |ω|=|?(z)|→ ∞,|z|→ ∞,因此,對(duì)上述的Rε,存在R′＞ 0,當(dāng) |z|＞ R′時(shí),有 |ω|=|?(z)|＞ Rε.于是對(duì)上述的 ε,取 R=R′,當(dāng) |z|＞ R 時(shí),|ω|=|?(z)|＞ Rε且

當(dāng)|a|=0時(shí),?(z)=b,由上述情形易知,這時(shí)(2.4)式仍然成立.

由(2.4)式容易得到

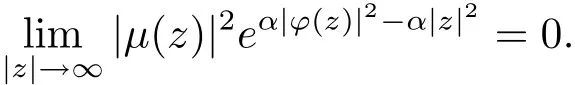
再由引理2.6知|a|＜1.

(iii)?(i).設(shè){fn}為中任意有界且在C的任一緊子集上一致收斂于0的序列,則存在C1＞0,使得‖fn‖≤C1.由于μ∈,則存在C2＞0,使得‖μ‖2,m≤C2.若存在常數(shù)a,b∈C,|a|＜1,使得?(z)=az+b,z∈C.令ω=?(z),當(dāng)0＜|a|＜1時(shí),

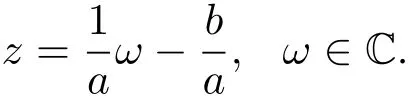
由(2.4)式,對(duì)任意的ε＞0,存在R＞0,當(dāng)|z|＞R時(shí),

那么取N=Nε,當(dāng)n＞N 時(shí),有

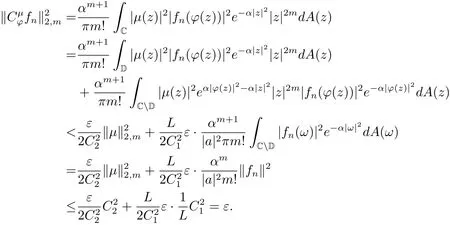
當(dāng)|a|=0時(shí),?(z)=b,此時(shí)有

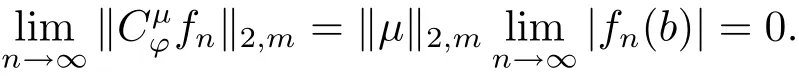
接下來討論Hilbert空間上的一類重要算子–Hilbert-Schmidt算子.文獻(xiàn)[8]給出了Fock空間F2上的加權(quán)復(fù)合算子是Hilbert-Schmidt算子的完全刻畫,其證明過程可以平行地推廣到Cn上的Fock空間.下面給出空間上的加權(quán)復(fù)合算子是Hilbert-Schmidt算子的一個(gè)充分必要條件.

定理2.3設(shè)?是C上的解析自映射,μ∈H(C),0＜α＜∞,若有界,則是上的Hilbert-Schmidt算子的充分必要條件為

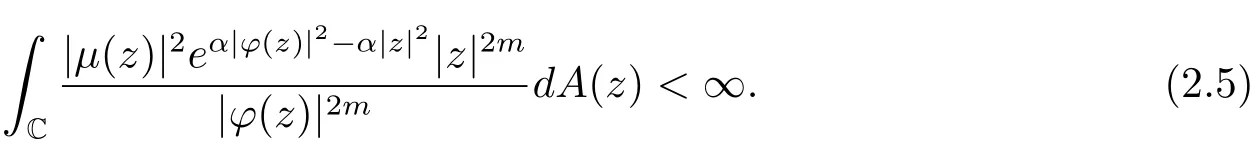
證設(shè)(2.5)式成立,記en為的規(guī)范正交系,則

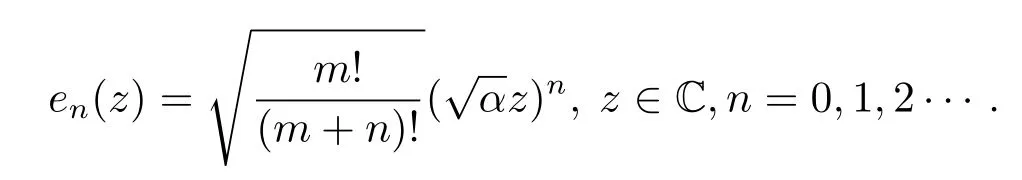
從而

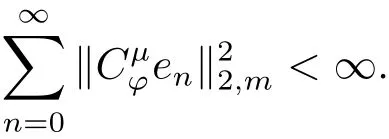
由上述證明過程有

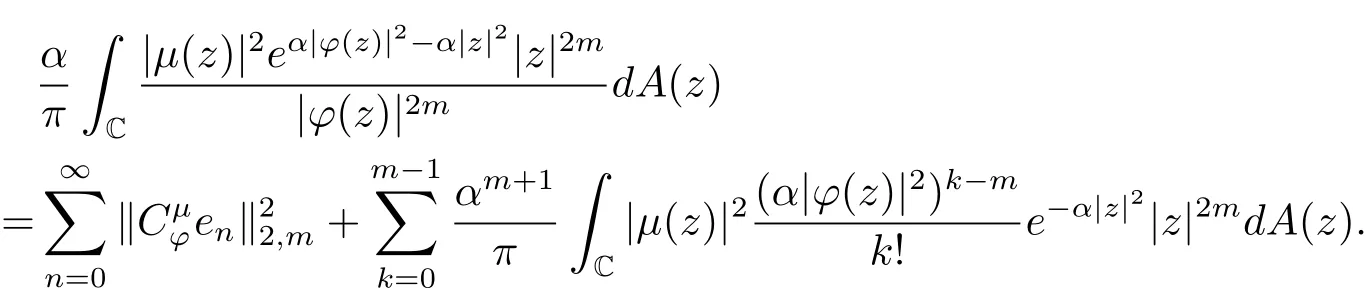
顯然,要得到(2.5)式,只需上式等號(hào)右邊第二項(xiàng)有界即可.為此,令

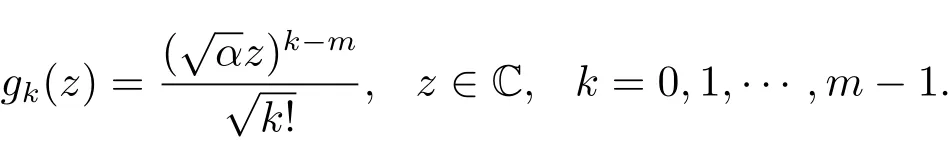
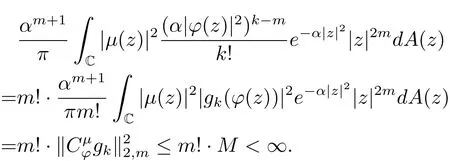
進(jìn)而有

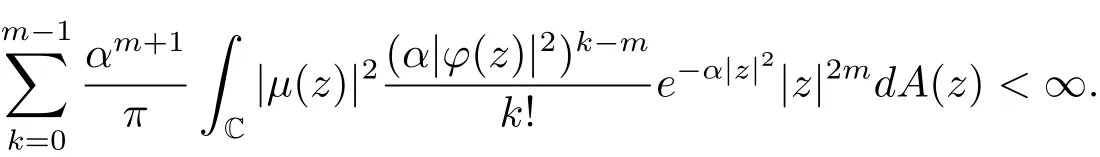
故(2.5)式成立.