趙海燕, 劉曉俊

(上海理工大學 理學院,上海 200093)

涉及實零點的亞純函數的Picard 型定理Ⅱ

趙海燕, 劉曉俊

(上海理工大學 理學院,上海 200093)

超越亞純函數; 實零點;Picard型定理; 正規(guī)族

1 問題的提出

1959年,Hayman[1]證明了如下的Picard型定理:

定理1 設f是復平面C上的亞純函數,k∈+,若f≠0,且f(k)≠1,則f≡常數.

1979年,顧永興[2]證明了對應的正規(guī)定則:

定理2 設F為區(qū)域D內的亞純函數族,k∈+,若對任意f∈F,f≠0,且f(k)≠1,則F在D內正規(guī).

2013年,童曉麗等[3]從另一方面將定理2中的限制條件“f≠0”減弱為“f的零點分布在一條直線上”,得到定理3.

定理3 設F是定義在單位圓盤D上的亞純函數族,若存在M≥0,使得對任意的f∈F,有:

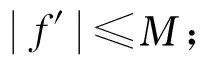
b.f的零點分布在一直線上;

c.f的極點重級m≥3;

d.f′≠1.

則F在D上正規(guī).

2015年,洪蘇敏等[4]又將定理3中的條件“f′≠1”改為“f′≠zd”,得到定理4.

定理4 設d∈+,F是定義在單位圓盤D上的亞純函數族,若存在M≥0,使得對任意的f∈F,有:

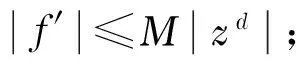
b.f的零點分布在一直線上;

c.f的極點重級m≥3;

d.f′≠zd.

則F在D上正規(guī).

2003年,Bergweilier等[5]將定理1中的條件“f(z)≠0”減弱為“f的零點和極點除有限多個外都是重級的”,并把例外值推廣到“不恒為零的有理函數”,得到定理5.

定理5 設f是一個超越亞純函數,R是一個有理函數,且R?0,f的零點和極點除有限多個外都是重級的,則f′-R有無窮多個零點.

2016年,徐成雨等[6]在定理5的基礎上,把“f的零點是重級的”減弱為“f只有實零點”,得到了例外函數是多項式的Picard型定理6.

定理6 設d∈+,f是復平面C上的超越亞純函數,若存在M≥0,使f滿足:

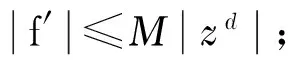
b.f的零點均為實數;

c.f的極點重級至少為3.

則f′-zd有無窮多個零點.

本文在定理6的基礎上進一步考慮例外函數是有理函數的情況,得到定理7.

定理7 設f是復平面C上的超越亞純函數,若存在M≥0,使f滿足:

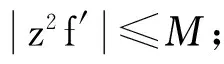
b.f的零點均為實數;

c.f的極點重級至少為3.

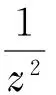
定理8 設F是定義在單位圓盤Δ上的亞純函數族,若存在M>0,使得對任意的f∈F,有

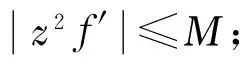
b.f的零點均為實數;

c.f的極點重級至少為3;

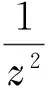
則F在Δ上正規(guī).

2 主要引理

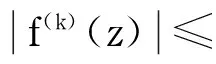
a.點列zn→z0;

b.函數列fn∈F;

c.正數列ρn→0+.

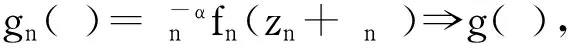
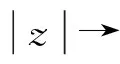
由Ahlfors-Shimizu特征函數[8-9]的表達式可知,若g為Julia例外函數,則當r→時有T(r,g)=O((logr)2).

引理2[5]設g是一個亞純函數,但不是Julia例外函數,則存在C上的點列{an},當n→時,有an→,g(an)→0,ang′(an)→.

引理3[5,10]超越Julia例外函數沒有漸近值.

引理4[11]設F={fn}為單位圓盤Δ上的亞純函數族,k∈+,{bn}是Δ上的全純函數列,且在Δ上,bn1,若則F在Δ上正規(guī).

引理5[5]設f為超越亞純函數,R是一個有理函數,滿足:當z→時,R(z)～czd,這里c∈C(〗0},d∈.若f′-R僅有有限多個零點,且r→時令g(z):=,當d=-1時,g:=f,則g有一個漸近值.

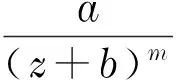
3 定理7的證明

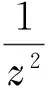
故由引理2知,存在點列{an},當n→時,有an→,g(an)→0,ang′(an)→,從而有anf(an)=.

設an=xn+iyn,下面分兩種情形討論.

情形1 假設xn→x0∈R,yn→.

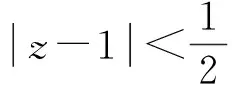
又因為

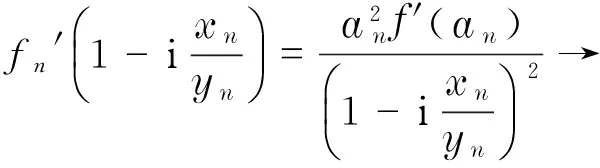
故

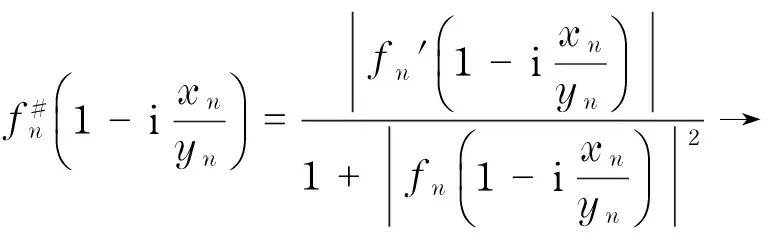
又由于當n→時,1-i→1,由Marty正規(guī)定則知,{fn(z)}在z=1處不正規(guī),矛盾.

情形2xn→,下面再分兩種情形討論.

令fn(z)=iynf(iynz),處理方法如上,同樣可得出矛盾.

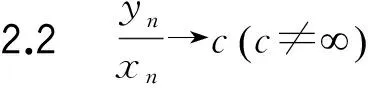
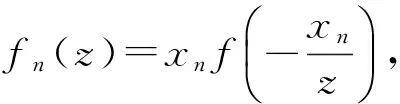
又因為

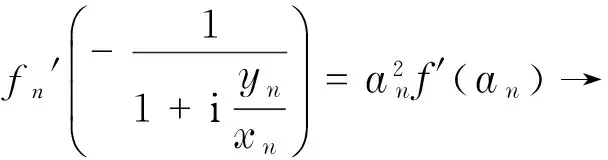
故

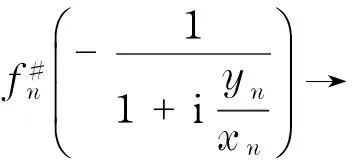
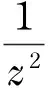
4 定理8的證明

4.1 在證明定理8之前先證明一個引理

引理7 設{fn}是復平面C上的一族亞純函數,fn的零點均為實數,極點重級至少為3,若存在M>0,使fn滿足:

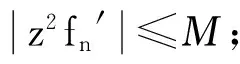
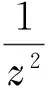
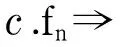
則f≡常數.

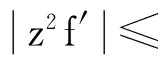
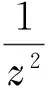
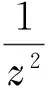
由定理7知f(z)為有理函數,分兩種情形討論.

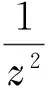
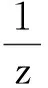
由于f不是常數,fn?f,且f(0)=,f(z)?,故由Hurwitz定理知存在zn→0,使得fn(zn)=.又因為fn(0)≠,故zn≠0.

因為上式兩端都是整數,故對充分大的n有

由幅角原理可知

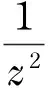
從而f≡常數,引理得證.

4.2 定理8的證明

由定理3的證明知F在Δ′上正規(guī),只需要證明F在z=0處正規(guī)即可.令F1={H=z2f:f∈F},對任意的f∈F,由定理條件知f′(0)≠,因此f(0)≠,所以對任意的H∈F1,H(0)=0,顯然F1在Δ′上正規(guī).下面證F1在z=0處正規(guī).

假設F1在z=0處不正規(guī),由引理1知,存在點列zn→0,正數列ρn→0+,函數列{Hn}∈F1,使得

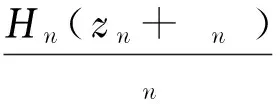
其中,g(ζ)為非常值有窮級亞純函數,且滿足g#(ζ)≤g#(0)=M+1.

然后分情形討論.

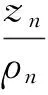
斷言:

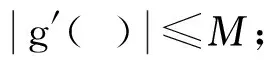
b.g′(ζ)≠1;

c.g(ζ)的零點在一直線上.

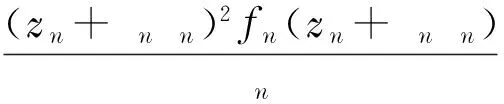
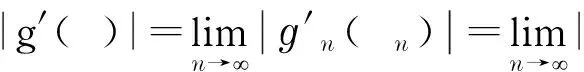
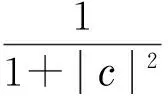
得

(zn+ρnζ)2fn′(zn+ρnζ)=

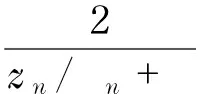
再由Hurwitz定理知存在點列ζn,ζn→ζ0,當n充分大時有(zn+ρnζn)2fn′(zn+ρnζn)=1.這與定理條件矛盾,故斷言b得證.

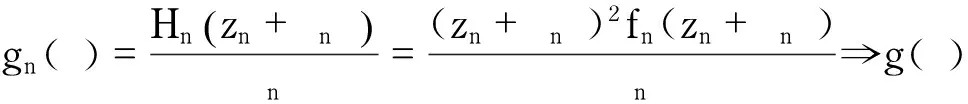
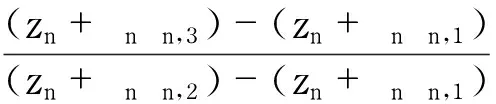
顯然 ,g(ζ)的極點重級至少為3.故由定理3的證明知上述g(ζ)不存在.

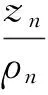
令

則g(ζ-α)在ζ=0處的零點重級至少為2,所以G(0)≠.

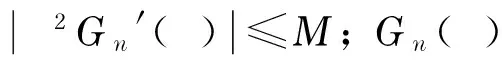
令G≡c(c為常數),由于g為非常值亞純函數,故c≠0,由Gn(ζ)=ρnfn(ρnζ)知,當n→時fn(0)=→,下面再分兩種情形討論.

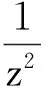
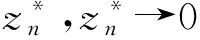
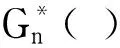
所以F1在z=0處正規(guī),所以F1在區(qū)域Δ上正規(guī).

下證F在Δ上正規(guī).任取{fn(z)}∈F,令Hn(z)=z2fn(z),則{Hn(z)}∈F1,又由于F1在z=0處正規(guī),所以存在{Hn(z)}的子列(仍記為{Hn(z)}),η>0,使得{Hn(z)}在Δ(0,η)上按球距內閉一致收斂于一個亞純函數H(z).由于fn(0)≠,所以Hn(0)=0,令n→得H(0)=0.所以存在η1>0,使得對任意的z∈Δ(0,η1)有由于{Hn(z)}在上按球距內閉一致收斂于H(z),所以對任意的有對任意的有fn(z)≠,所以fn(z)在上解析. 而在上由最大模原理知在上由Montel正規(guī)定則知,F在上正規(guī).又由定理3的證明知,F在Δ′上正規(guī),因此F在上正規(guī).定理得證.

[1]HAYMANWK.Meromorphicfunction[M].Oxford:ClarendonPress,1964.

[2]GUYX.Anormalcriterionofmeromorphicfamilies[J].ScientiaSinica,MathematicalIssue(I),1979,1:267-274.

[3] 童曉麗,劉曉俊.零點位于直線上的亞純函數的正規(guī)定則[J].上海理工大學學報,2014,36(4):362-365.

[4] 洪蘇敏,劉曉俊.零點分布在直線上的亞純函數的正規(guī)定則[J].上海理工大學學報,2016,38(3):211-217.

[5]BERGWEILERW,PANGXC.Onthederivativeofmeromorphicfunctionswithmultiplezeros[J].JournalofMathematicalAnalysisandApplications,2003,278(2):285-292.

[6] 徐成雨,劉曉俊.涉及實零點的亞純函數Picard型定理[J].上海理工大學學報,2016,38(5):414-418.

[7]PANGXC,ZALCMANL.Normalfamiliesandsharedvalues[J].BulletinofLondonMathematicalSociety,2000,32(3):325-331.

[8] 顧永興,龐學誠,方明亮.正規(guī)族理論及其應用[M].北京:科學出版社,2007.

[9] 楊樂.值分布論及其新研究[M].北京:科學出版社,1982.

[10]LEHTOO,VIRTANENKL.Onthebehaviourofmeromorphicfunctionsintheneighbourhoodofanisolatedsingularity[J].AnnalsoftheAcademyofScienceFenn,SeriesA,1957,240:1-9.

[11]PANGXC,YANGDG,ZALCAMANL.Normalfamiliesandomittedfunctions[J].IndianaUniversityMathematicsJournal,2005,54(1):223-236.

[12]WANGYF,FANGML.Picardvaluesandnormalfamiliesofmeromorphicfunctionswithmultiplezeros[J].ActaMathematicaSinica,1998,14(1):17-26.

(編輯:丁紅藝)

Picard Theorem Ⅱ of Meromorphic Functions with Real Zeros

ZHAO Haiyan, LIU Xiaojun

(CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

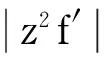
transcendentalmeromorphicfunction;realzeros;Picardtheorem;normalfamily

1007-6735(2017)04-0307-06

10.13255/j.cnki.jusst.2017.04.001

2016-11-15

國家自然科學基金青年基金資助項目(11401381)

趙海燕(1990-),女,碩士研究生.研究方向:復分析.E-mail:919004902@qq.com

劉曉俊(1982-),男,副教授.研究方向:復分析.E-mail:xiaojunliu2007@hotmail.com

O

A