Li Jibin(1.Schoolof Mathematical Sciences,Huaqiao University,Quanzhou 362021,China; 2.Departmentof Mathematics,Zhejiang NormalUniversity,Jinhua 321004,China)

The existence of n-order algebraic curve solutions ofplanar quadratic polynomialsystems

Li Jibin1,2
(1.Schoolof Mathematical Sciences,Huaqiao University,Quanzhou 362021,China; 2.Departmentof Mathematics,Zhejiang NormalUniversity,Jinhua 321004,China)

In this shortarticle,we show that for any given positive integer n≥2,there is a planar quadratic differentialsystem having n-degree and 2n?degree classicalalgebraic curve solutions.

quadratic differentialsystem;algebraic curve solution;periodic solution;integrable system

2010 MSC:14H50,34C25,35Q72

1 Introduction

We are interested in the study of planar polynomialsystems,because they occur very often in applications. Indeed,such equations appear in modelling chemicalreactions,population dynamics,travelling wave systems of nonlinear evolution equations in mathematical physics and in many other areas of applied mathematics and mechanics.From the mathematicalpointofview,quadratic systems are perhaps the mostsimple nonlineardifferential systems.Despite their simplicity,there are important open questions around them.It is a particular case of the famous Hilbert′s 16th problem[1].

More recently,Garcia and Llibre[2]gave a lot of examples to show that classical planar algebraic curves are realizable by quadratic polynomialdifferentialsystems.We say thata given algebraic curve is realized by a quadratic system when this algebraic curve is an invariantcurve solution ofa system

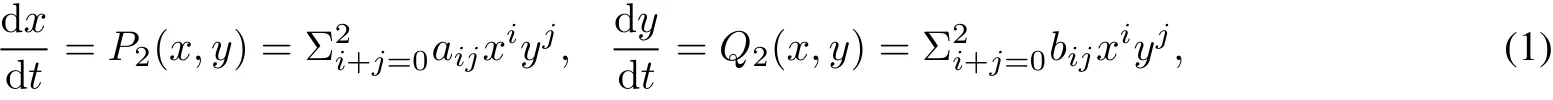
where aijand bijare constantparameters.

Itis wellknown thatany cubic algebraic curve is always realized by some quadratic Hamiltonian system[3?4]. Quadratic systems realizing classicalquadratic and higherdegree algebraic curves have been found.

For a given positive integer n,is there an n-degree algebraic curve such thatitis realizable by quadratic polynomialdifferentialsystems?In this paper,we show the following conclusion.

Theorem 1 For any given positive integer n≥2,there is a planar quadratic differentialsystem having ndegree and 2n?degree classicalalgebraic curve solutions.

The proofof this theorem is given in section 2.

2 An integrable quadratic system having n-degree classicalalgebraic curve solution

Consider the quadratic differentialsystem

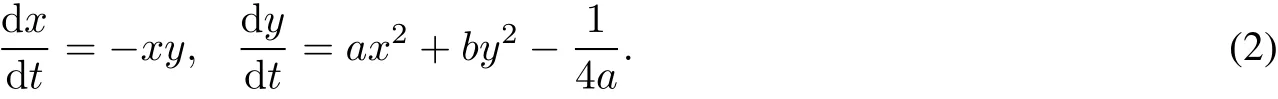
This is an integrable system with the firstintegral

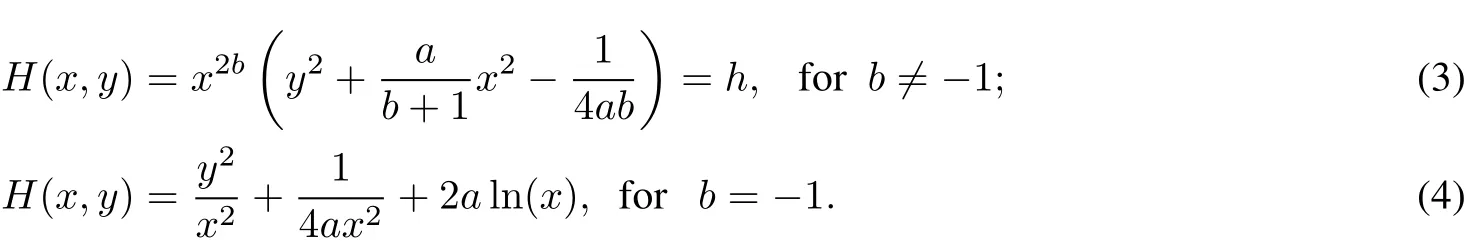
We only considerthe case a＞0.Otherwise,we applythe transformation x→?x,y→?y.

Clearly,system(2)alwayshastwo singularpoints E.When ab＞0,there existtwo singularpoints?in the straightline x=0.

Let M(xj,y)be the coefficientmatrix ofthe linearized system forequation(2)ata singularpoint.We have

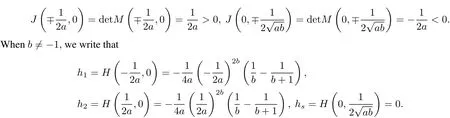
By using the above information,we have the following qualitative analysis.

Lemma 1 The planar quadratic system(2)has two symmetric centers with respectto the y?coordinate axis, for which there existexactly three topologicalphase portraits shown in Figs.1(a),1(b)and 1(c).

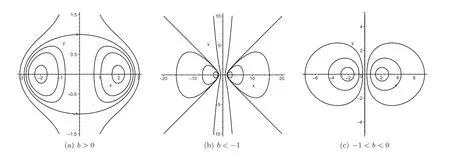
Figure 1 The phase portraits of the system(2)for a＞0

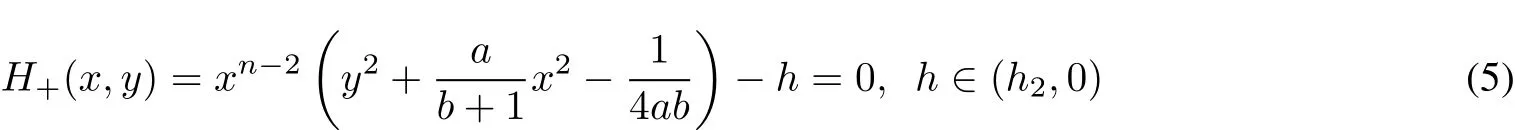
give rise to two periodic solutions ofsystem(2),see Fig.1(a).

Lemma 3 Take a＞0,b=?n＜?1,where n is a positive integer.Then the 2n?degree algebraic curves defined by

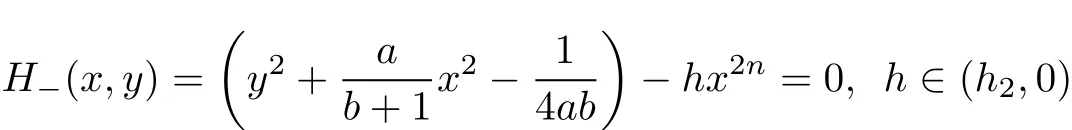
give rise to two periodic solutions ofsystem(2),see Fig.1(b).

Thus we have proved Theorem 1 by Lemma 2 and Lemma 3.

[1]Li J.Hilbert′s 16th problem and bifurcations of planar polynomial vector fields[J].Int J Bifurcation and Chaos,2003, 13:47-106.

[2]Garcia IA,Llibre J.Classicalplanar algebraic realizable by quadratic polynomialdifferentialsystem[J].IntJBifurcation and Chaos,2017,27,to appear.

[3]LiJ.Exactparametric representations oforbits defined by cubic Hamiltonian[J].JShanghaiNormalUniversity(NatSci), 2014,43(5):456–463.

[4]Smogorzhevskii A S,Stolova E S.Handbook of the theory of planar curves of the third order[M].Moscow:Fizmatgiz, 1961.

O 29 Document code:A Article ID:1000-5137(2017)03-0439-03

10.3969/J.ISSN.100-5137.2017.03.013

date:2017-03-17

This research was partially supported by the National Natural Science Foundation of China(No.1147 1289,11571318).

Li Jibin,professor,reseach area:dynamical systems,differential equation,solitons and chaos, E-mail:ijb@zjnu.cn