Option Pricing and Hedging under a Markov Switching Lvy Process Model
SONG Rui-li,WANG Bo
(School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing 210023, China)
Option Pricing and Hedging under a Markov Switching Lvy Process Model
SONG Rui-li,WANG Bo
(School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing 210023, China)
In this paper,we consider a Markov switching Lvy process model in which the underlying risky assets are driven by the stochastic exponential of Markov switching Lvy process and then apply the model to option pricing and hedging.In this model,the market interest rate,the volatility of the underlying risky assets and the N-state compensator, depend on unobservable states of the economy which are modeled by a continuous-time Hidden Markov process.We use the MEMM(minimal entropy martingale measure)as the equivalent martingale measure.The option price using this model is obtained by the Fourier transform method.We obtain a closed-form solution for the hedge ratio by applying the local risk minimizing hedging.
Markov chain model;MEMM;Lvy process;option pricing;hedging
§1.Introduction
In recent years,there is a considerable interest in the applications of regime switching models driven by a hidden Markov chain process to various financial problems.For an overview of hidden Markov chain processes and their financial applications[12].Some work on the use of hidden Markov chain models in finance includes[37].As a financial market model,we consider a Markov switching Lvy process model in which the risky underlying assets are driven by the stochastic exponential of Markov switching Lvy process.In this model,the market interest rate,the volatility of the underlying risky assets and the N-state compensator,depend onunobservable states of the economy which are modeled by a continuous-time Hidden Markov process.In this model,the market is incomplete in general,hence,the equivalent martingale measure is not unique.Markov switching Lvy process is discussed in[8]and there they obtained the minimal entropy martingale measure(MEMM)for Markov switching Lvy processes.Option pricing by using Fourier transform method were discussed in[912].
In the Black-Scholes model[13],the market is assumed to be complete so that a perfect hedge can be attained by delta hedging.However,generally in an incomplete market,a perfect hedge is not attainable.F¨ollmer and Schweizer[14]propose what they refer to as a local risk-minimizing method for constructing a portfolio containing options and underlying stocks that minimizing the variance based on the physical market measure.Boyarchenko and Levendorskii[15]discuss the local risk-minimizing hedging under the exponential Lvy stock price model and find an explicit form for the hedge ratio.
The purpose of this paper is threefold.First,we construct a Markov switching Lvy process model and then discuss the option pricing and hedging problems using this model.The model in our paper is different with the stochastic volatility model with a Lvy driving process in[11]. Second,we adopt the MEMM(minimal entropy martingale measure)as the risk neutral probability measure and provide the European option pricing formula under this measure.Finally, we apply locally risk-minimizing hedging for the Markov switching Lvy process model and present an explicit form for the hedge ratio.
The remainder of this paper is organized as follows.In section 2,the Markov switching Lvy process model is introduced and the MEMM is obtained.In section 3,we provide the option pricing formula for the model.In section 4,we obtained the closed-form solution for the hedge ratio by applying the local risk minimizing hedging under the model.
§2.Markov Switching Lvy Process Model
Let(?,F,P)be a complete probability space,where P is a real-world probability measure. Denote T the time index set of[0,T].Let(Lt)t∈Tbe a real-valued Lvy process.Then for any λ∈R,we have
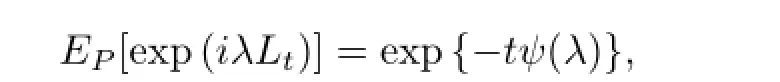
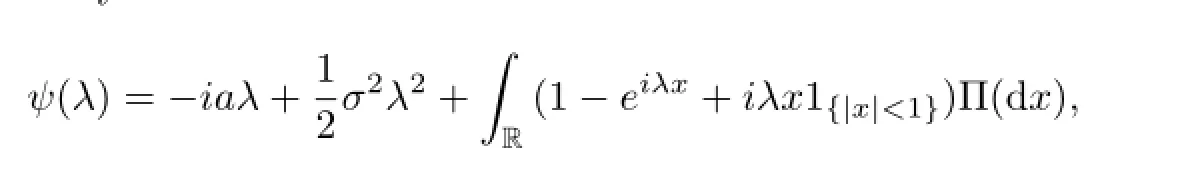
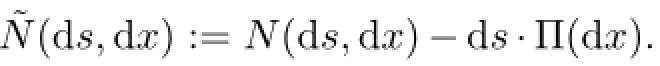
where(Wt)t∈Tis a one-dimensional standard Brownian motion.For the details of Lvy processes we can refer to[1617].
Suppose U={Ut,t≥0}is a Markov chain on the probability space(?,F,P),independent of process(Wt)t∈Tand(ΔLt)t∈Tand with a state space{e1,e2,···,eN},where
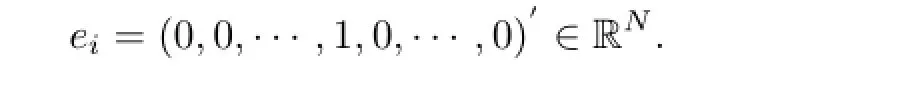
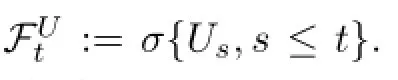
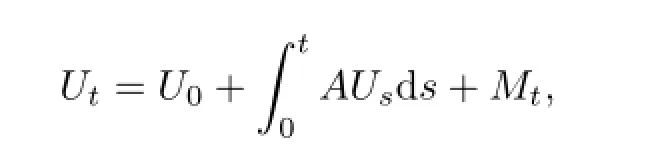
Now suppose for each integer j with 1≤j≤N,we have aj,σjand compensator measure Πj(d x)d t.
Let〈·,·〉denote the inner product operator and suppose that,under the probability P,the compensator of N is π(d s,d x),where
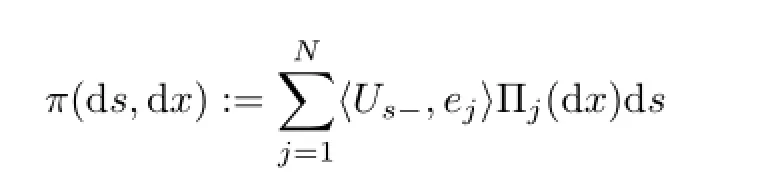
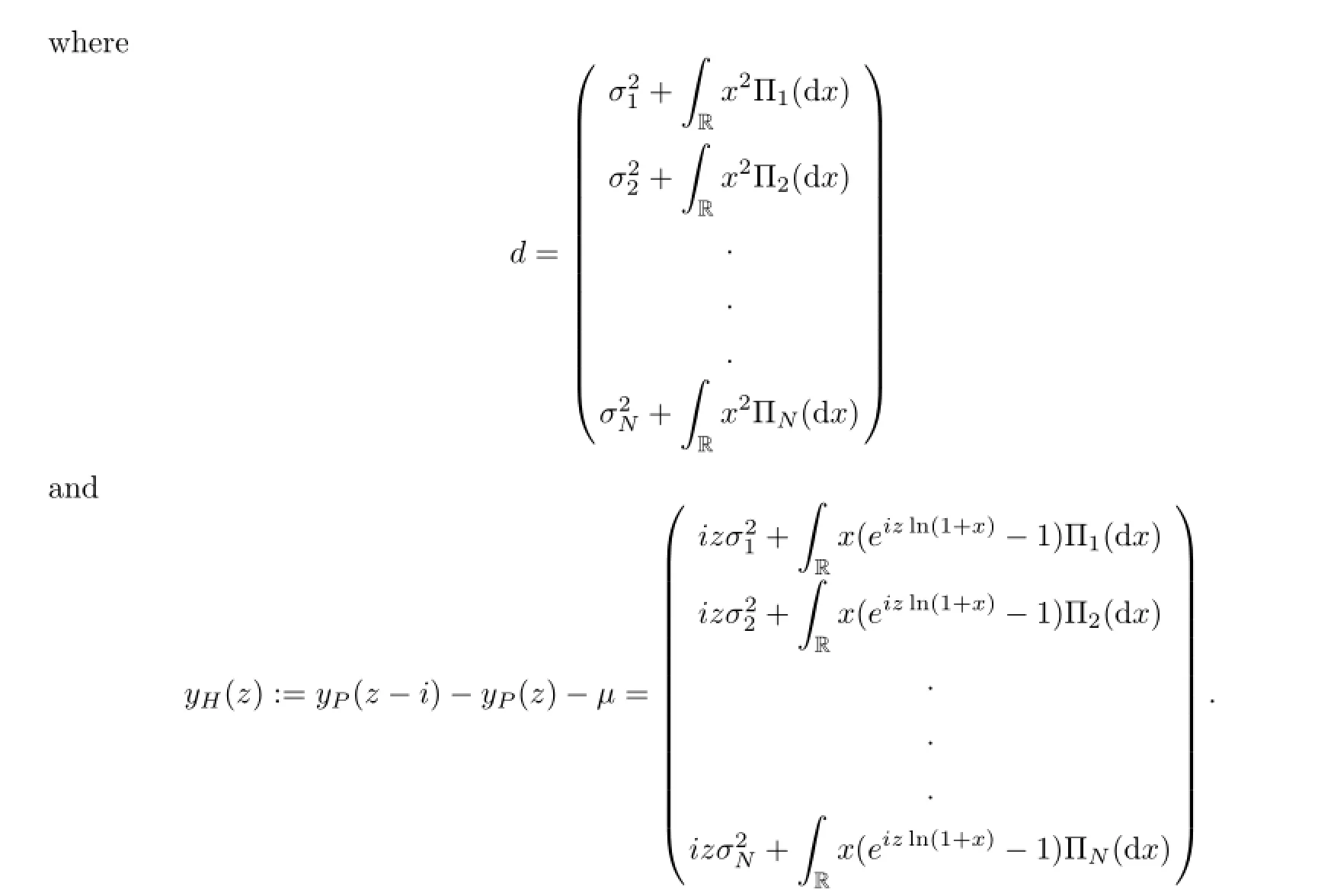
and with a=(a1,a2,···,aN)′∈RN,σ=(σ1,σ2,···,σN)′∈RN,the drift at time s is as:=〈Us,a〉and the volatility at time s is σs:=〈Us,σ〉.
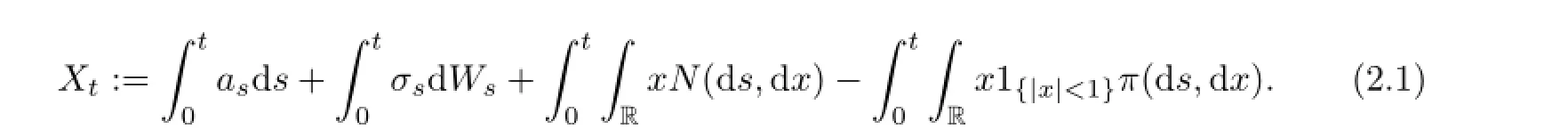
The dynamics of the stock price process{St}t∈Tis given by the following stochastic exponential of Markov switching Lvy process

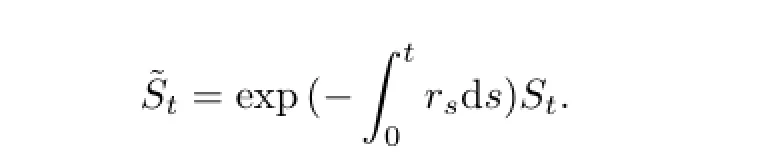
According to Theorem 4.1 in[8],the MEMM(minimal entropy martingale measure)of the discounted stock price process is obtained by the following theorem.
Theorem 2.1 If there is a θ=(θ1,···,θN)′∈RN,such that
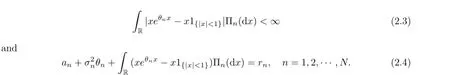
Thus define a probability measure Pθon Gtby means of the regime switching Esscher transform
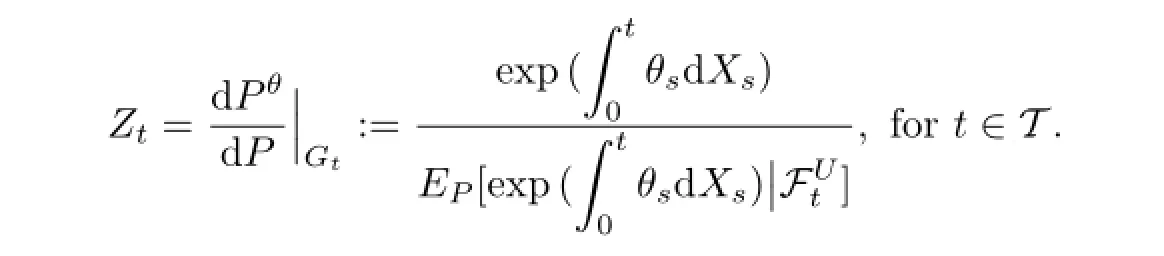
More concretely,

Then the probability measure Pθattains the MEMM for the discounted stock price process?S with respect to FUt.
§3.Option Pricing Under the Markov Switching Lvy Process Model
Because the hidden Markov chain has a countable state space,the amount of time that the volatility state stays on each state enfor n=1,2,···,N from 0 to time t is given as

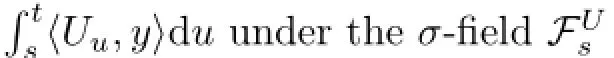
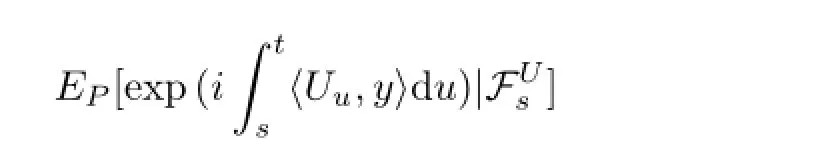
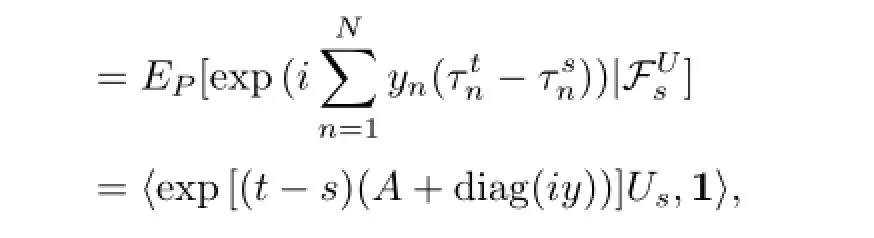
where 1=(1,1,···,1)′∈RN.
For the proof of Lemma 3.1,we can refer to Lemma 1[11].The y in Lemma 3.1 can be extended to complex field CN.
By(2.1)~(2.2)and(3.1),we have
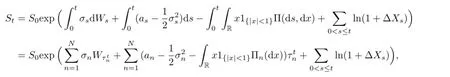
where ΔXs>-1(0<s≤t).Denote Yt=ln(St/S0).Then
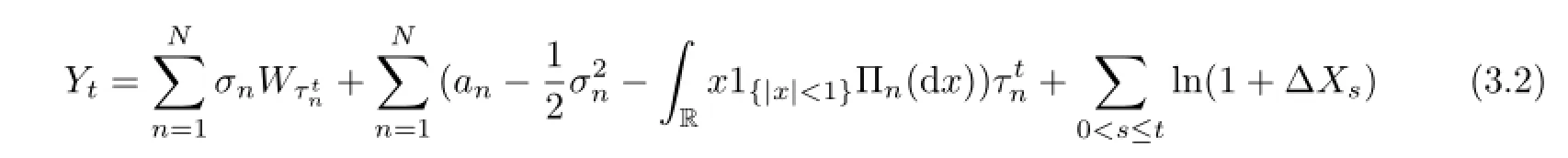
Lemma 3.2 Let u∈R,such that RR|1-eiuln(1+x)|Πn(d x)<∞for every n=1,2,···,N. Denote
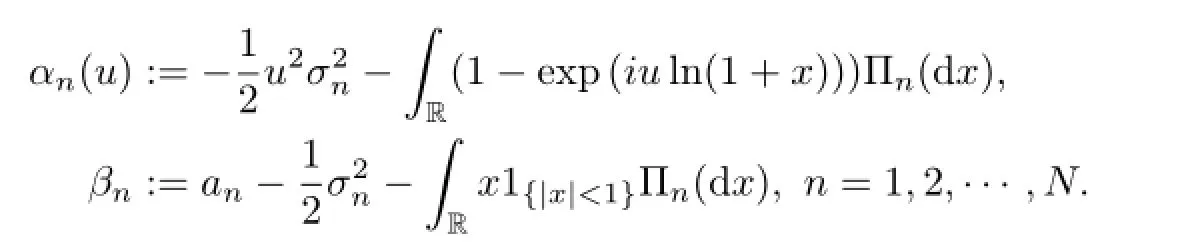
Let 0≤t≤T,the conditional characteristic function of YT-Ytunder measure P and the condition Gtis given by
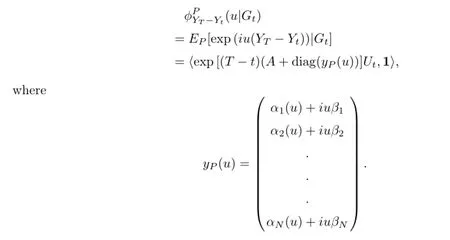

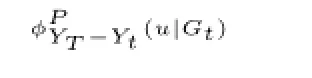
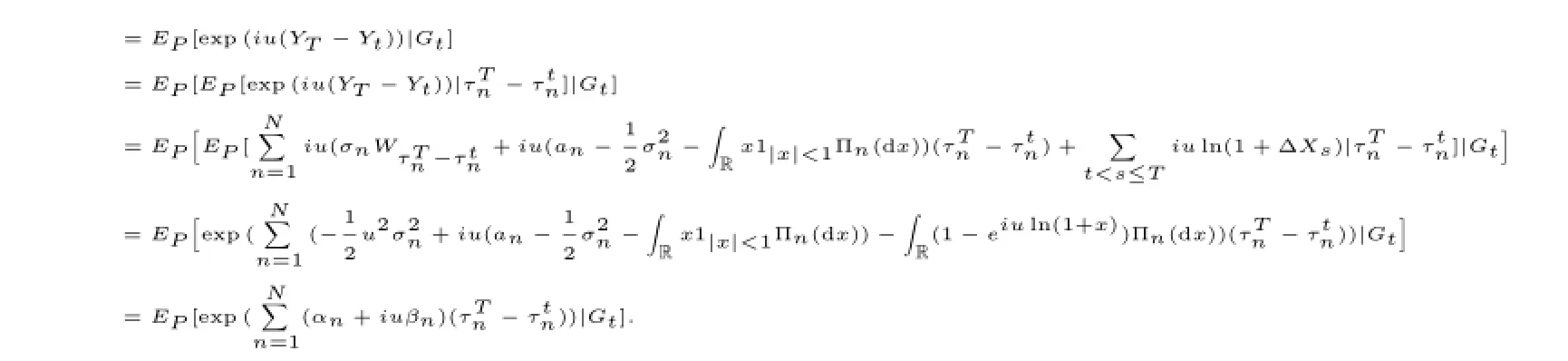
By Lemma 3.1,we have
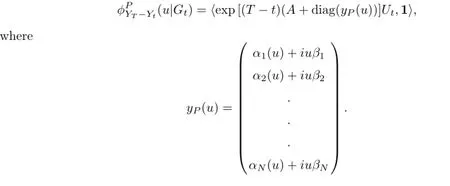
By(2.5)and(3.1),we have
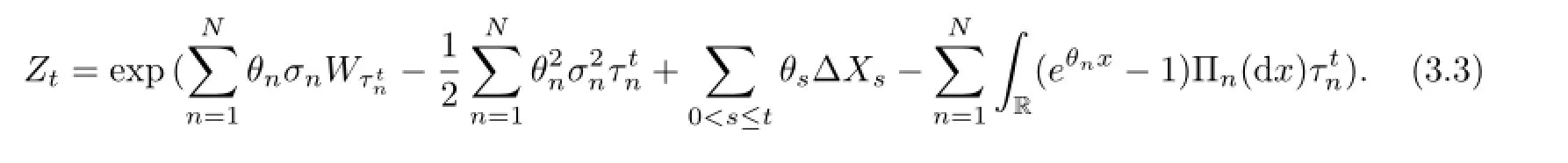
Lemma 3.3 Let θ=(θ1,θ2,···,θN)′∈RNsatisfy the conditions(2.3)and(2.4).Let u∈R,such that RR|1-eiuln(1+x)+θnx|Πn(d x)<∞for every n=1,2,···,N.Denote
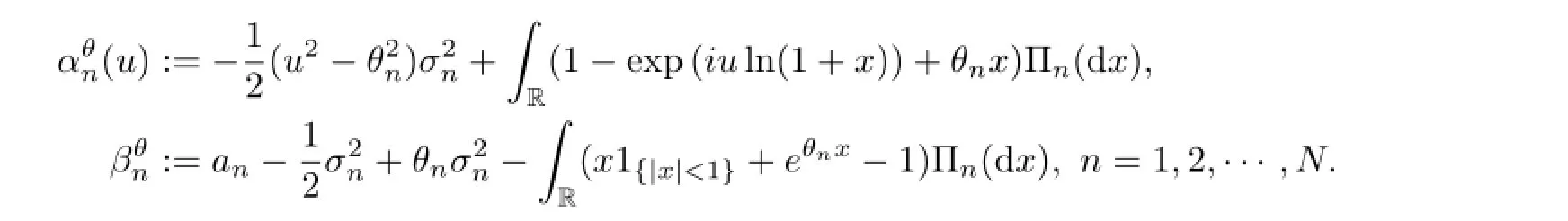
Let 0≤t≤T,the conditional characteristic function of YT-Ytunder measure Pθand the condition Gtis given by
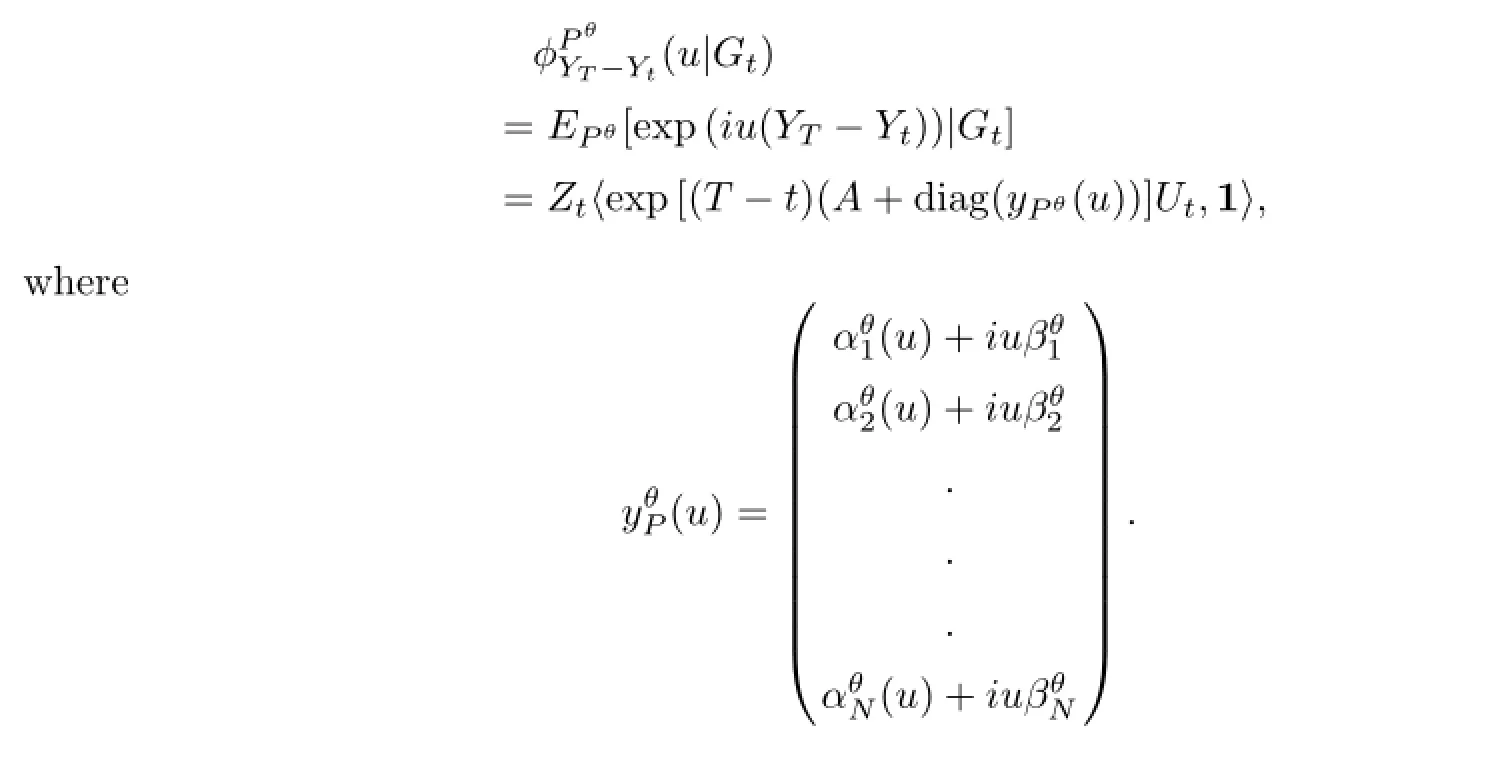
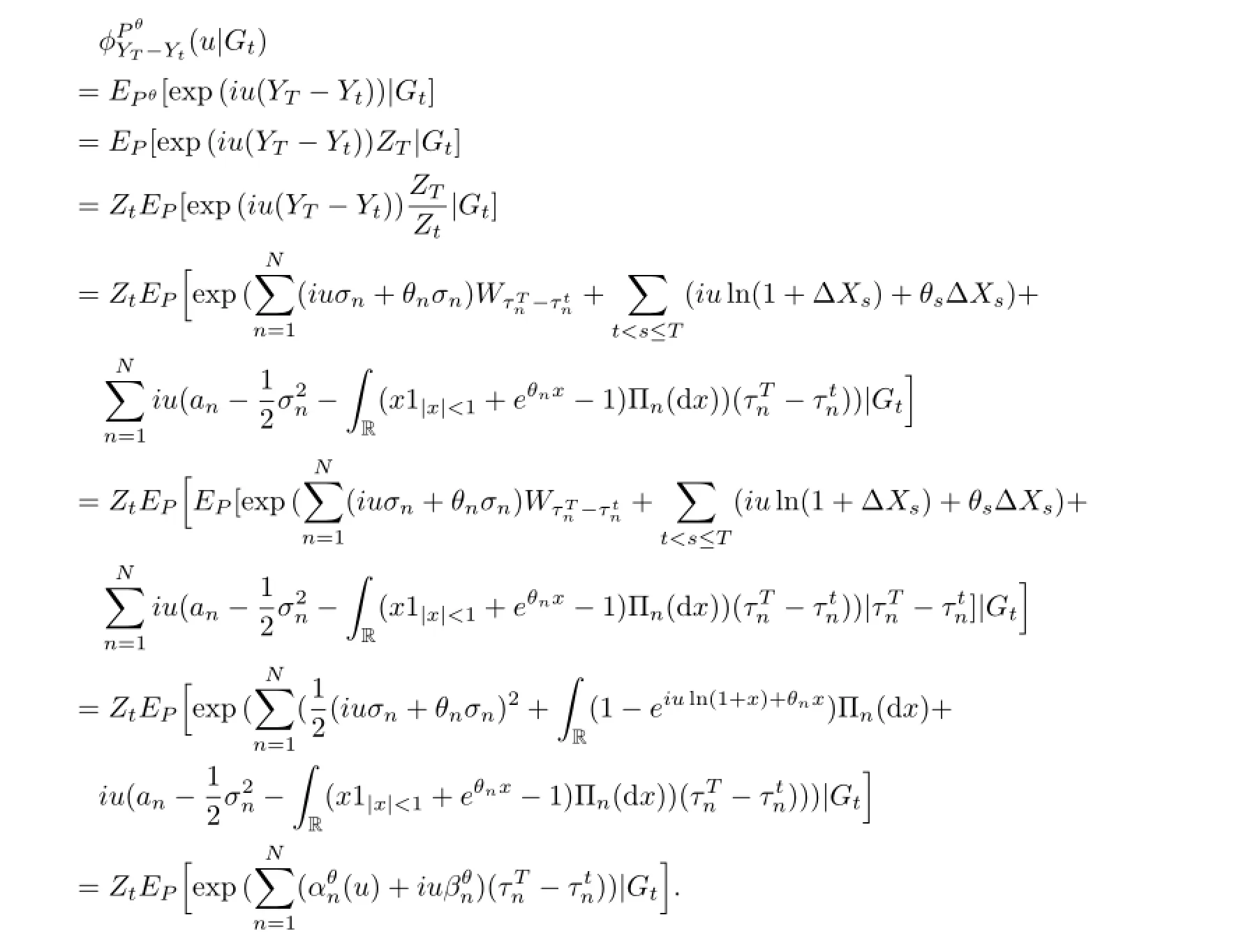
By Lemma 3.1,we have
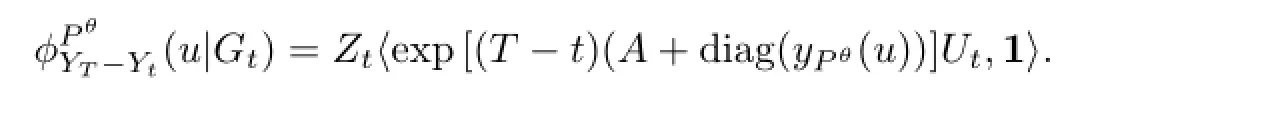
For convenience,we define a function on C×[0,∞)where C is the complex field that
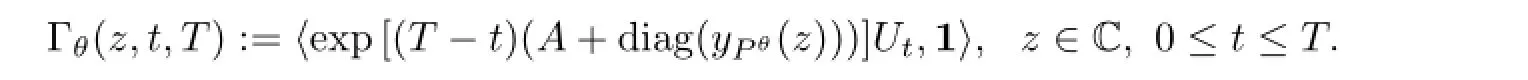
By Lemma 3.3,we have
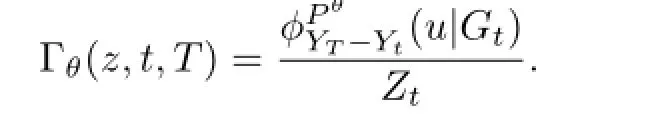
Let H(ST)be a payofffunction of one European option with time to maturity T,
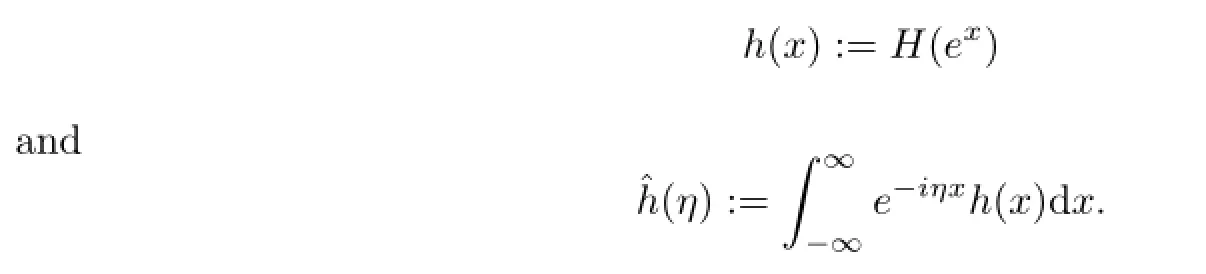
Suppose r=r1=r2=···=rNand?h(η)is defined for all η∈Rh,where Rh={z∈C|Im(z)∈Ih}for some real interval Ih.The characteristic function φPθYT?Yt(η)is defined for all η∈Rφ,
where Rφ={z∈C|Im(z)∈Iφ}for some real interval Iφ.Based on the no-arbitrage pricing framework,the European option price V with time to maturity T is given by
Theorem 3.1 Let θ=(θ1,θ2,···,θN)′∈RNwhich satisfies the condition(2.3)and(2.4). For v∈Ih∩Iφ,we have the European option pricing formula under the Markov switching Lvy process model by
using the complex inversion formula.
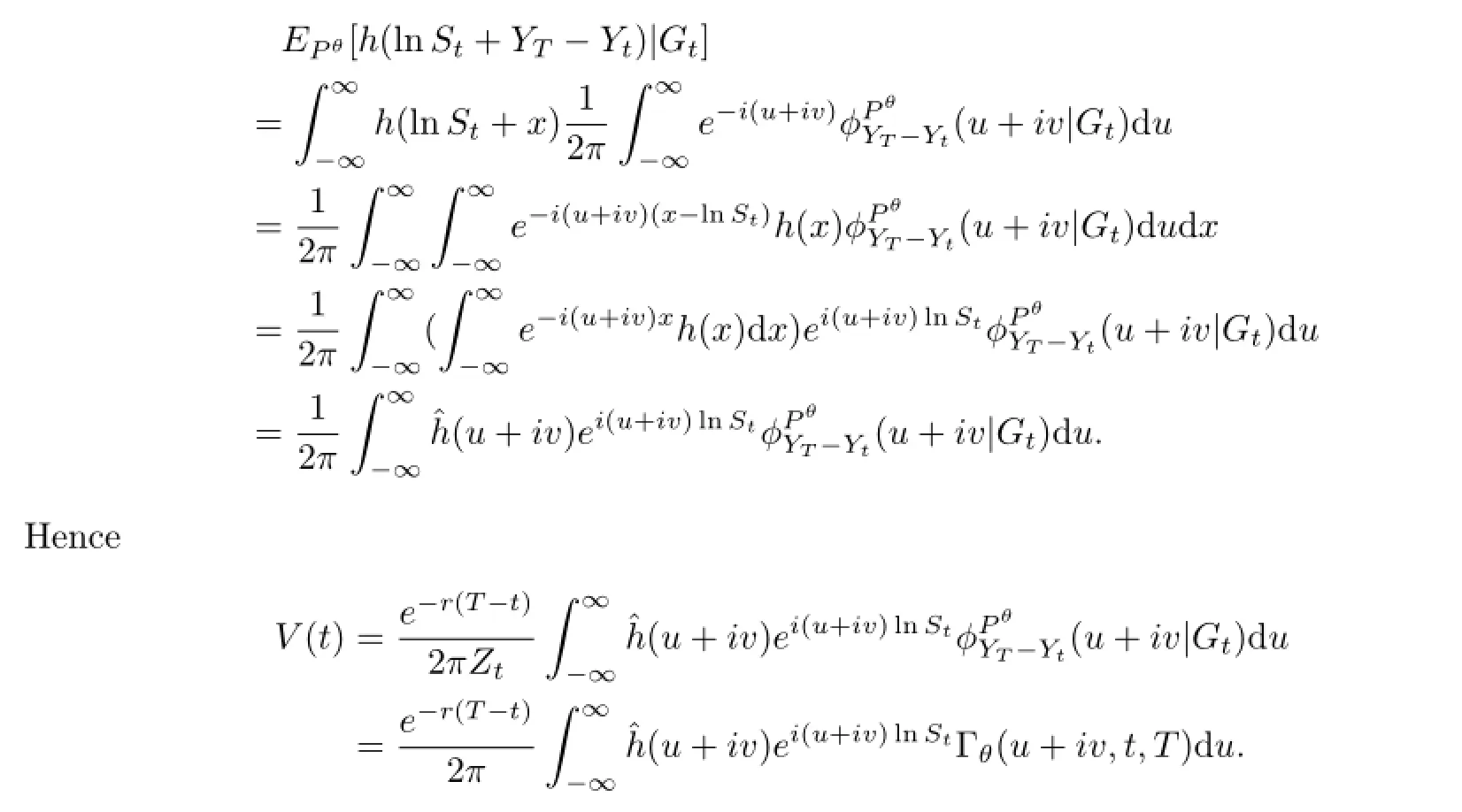
In particular,the payofffunction of a European call option with time to maturity T and strike price K is given by H(ST)=(ST-K)+and hence h(x)=(ex-K)+.Therefore,we have
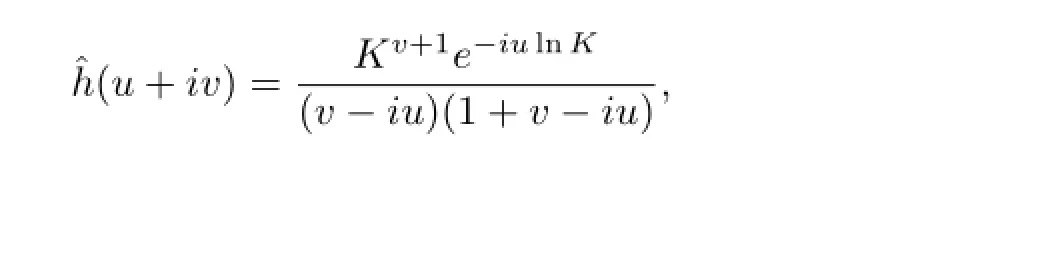
where v<-1.By Theorem 3.1,we have
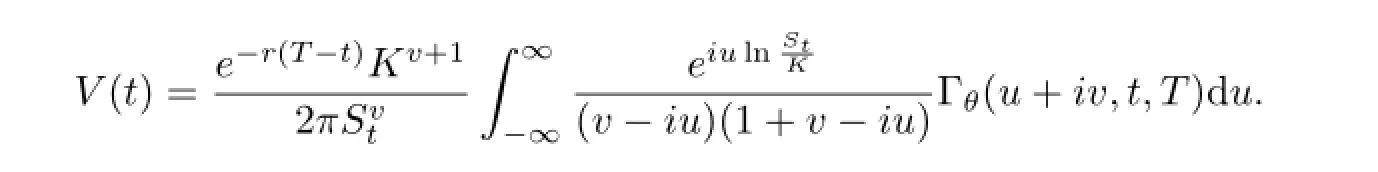
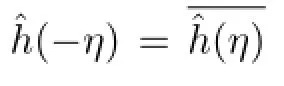
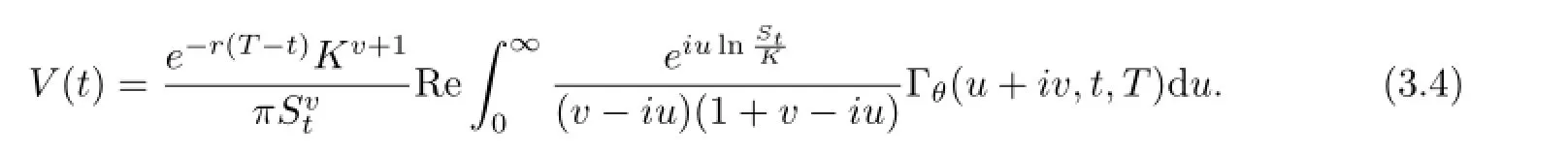
We can compute a European put option’s price in the same way as for a European call option. A European put option’s price can be obtained by the same formula as(3.4),but the condition of v is different:that is,v is positive real number.
§4.Local Risk-minimizing Hedge Ratio under Markov Switching Lvy Process Model
Consider a European option with maturity T>0 and let Vtbe the European option’s price at t.Let
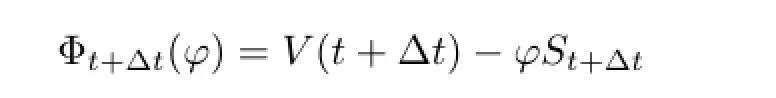
at time t<T.Let ?Δt(t)be the share of the underlying stock which minimizes variance of Φt+Δt(?).That is,
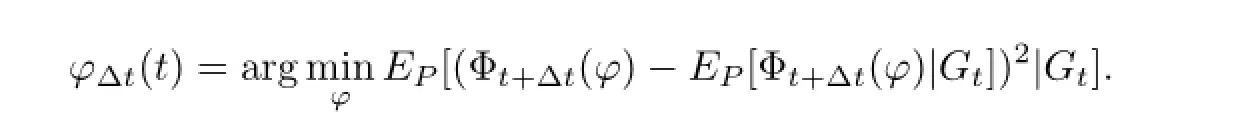
The locally risk-minimizing hedge ratio ?(t)at time t is defined as
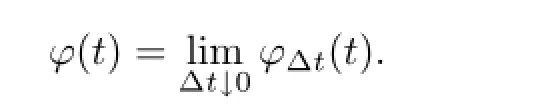
In this section,we assume that Ut+Δt=Utfor small Δt
Theorem 4.1 Let θ=(θ1,θ2,···,θN)′∈RNwhich satisfies the condition(2.3)and (2.4).Let v∈R satisfy RR|x|(|(1+x)?v|+1)Πnd x<∞for all n∈1,2,···,N.The locally risk-minimizing hedging ratio is equal to
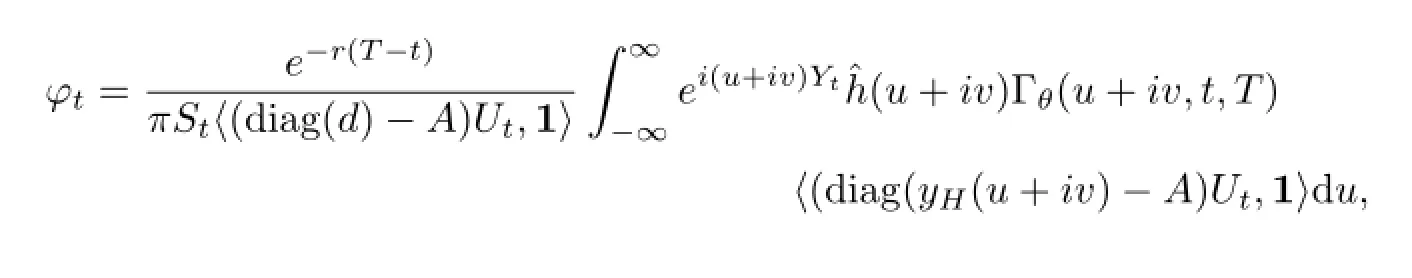
Proof Since we have
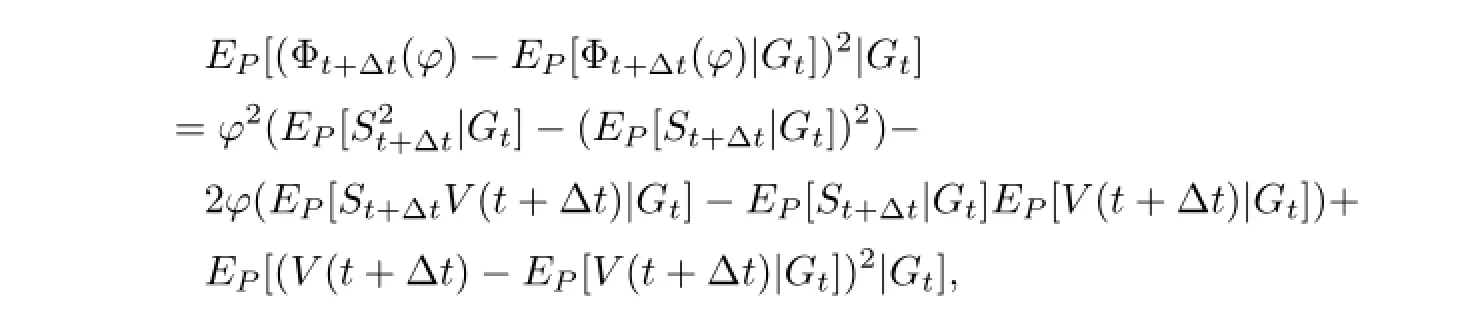
it minimizes at
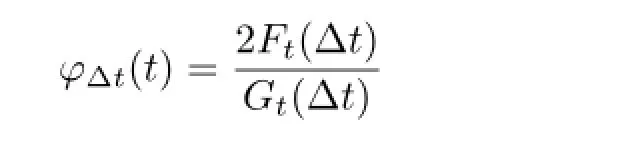
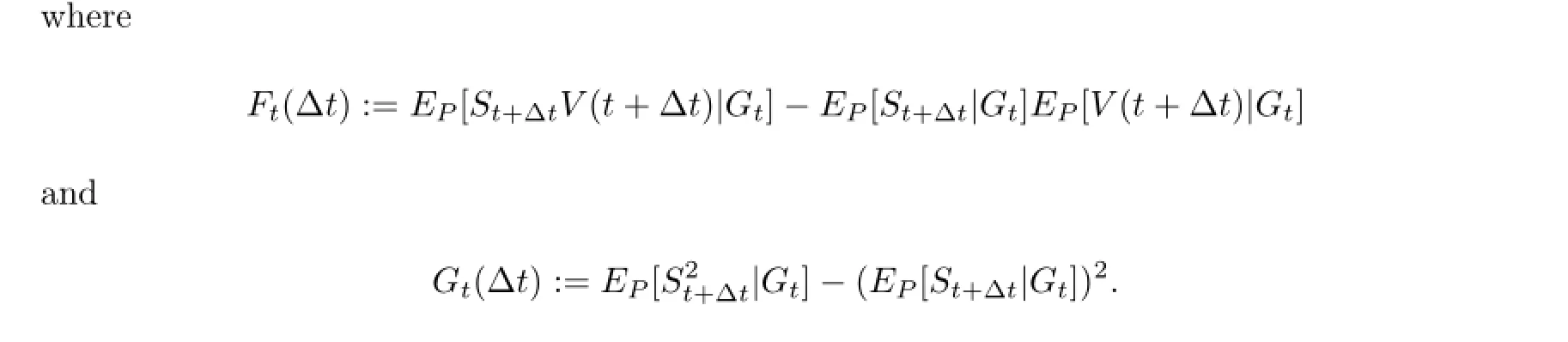
We have that
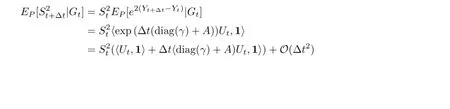
Hence we have
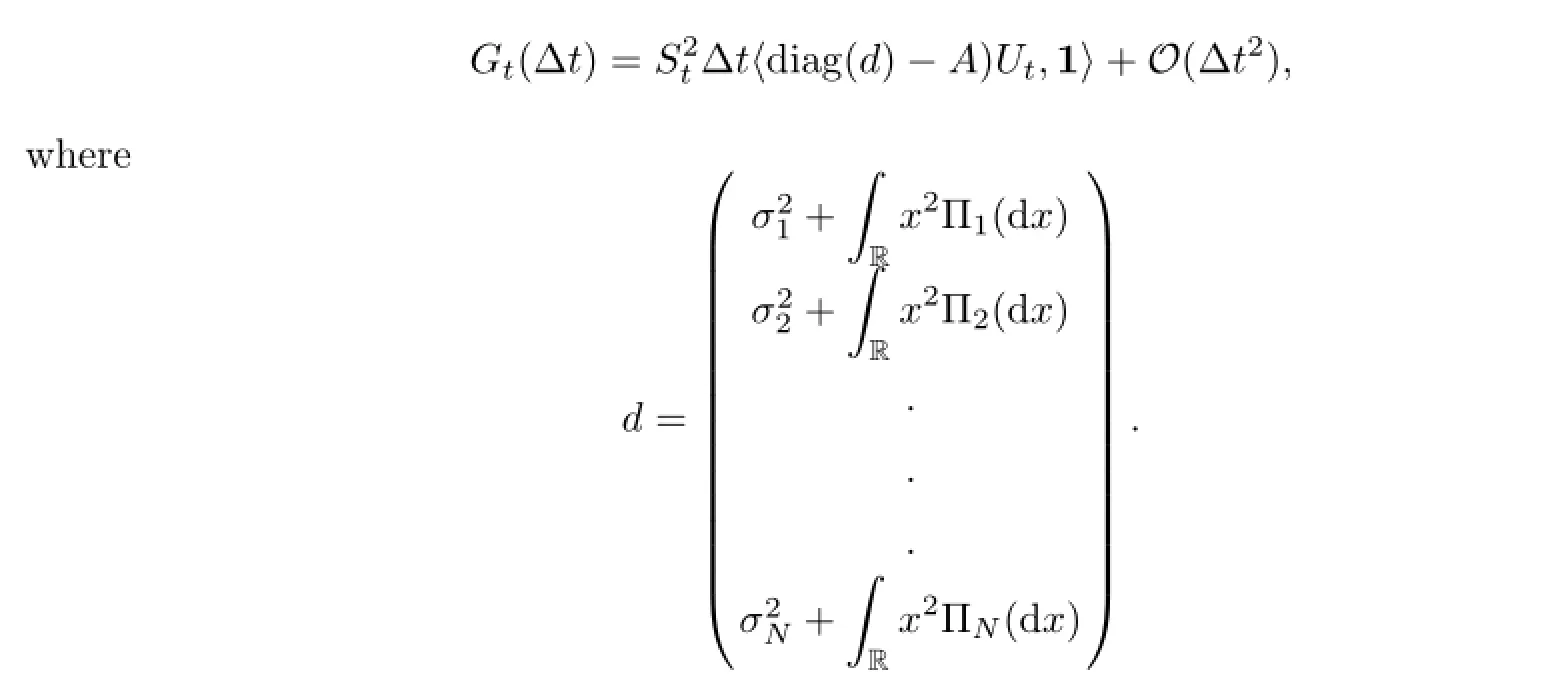
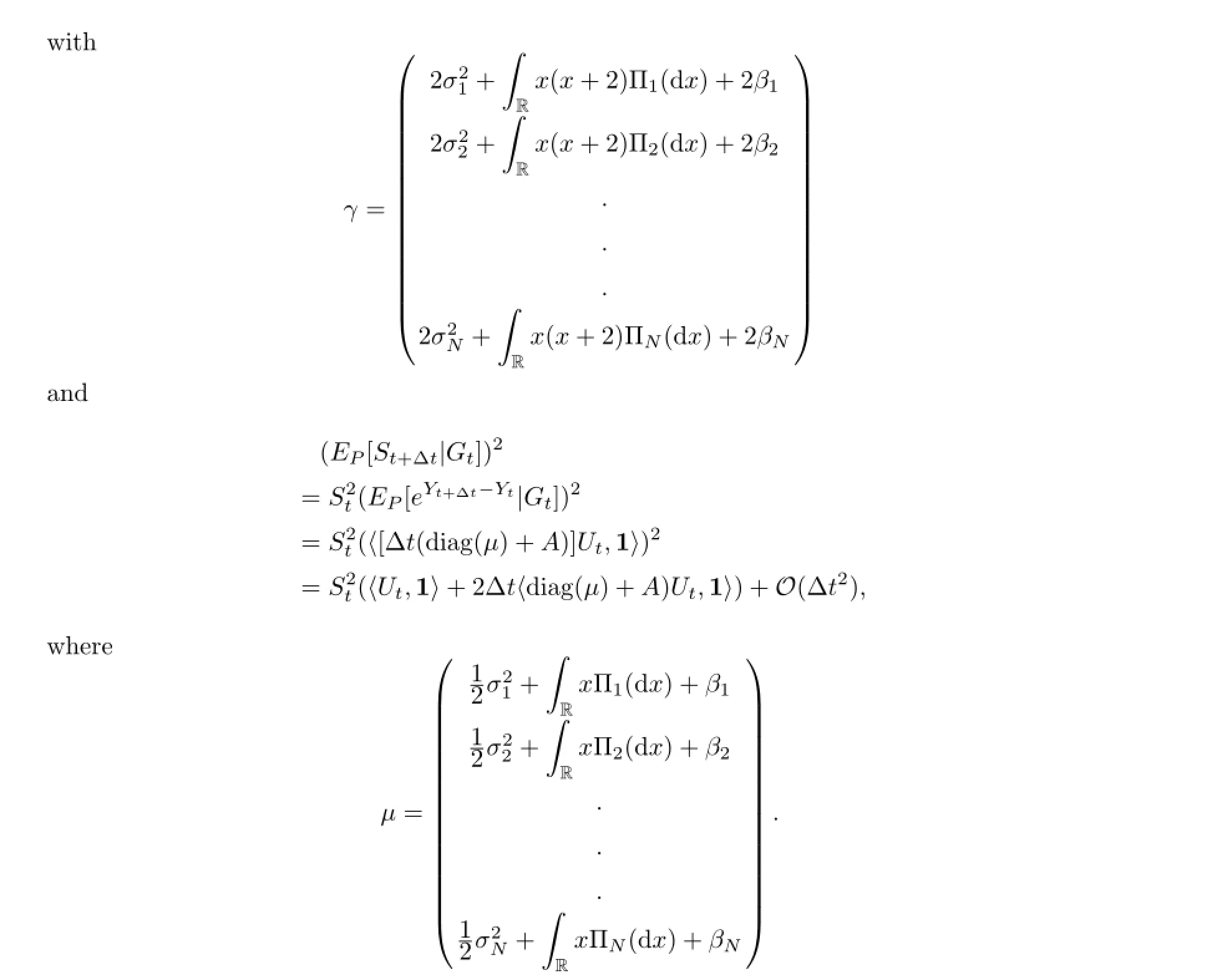
By Theorem 3.1,we have
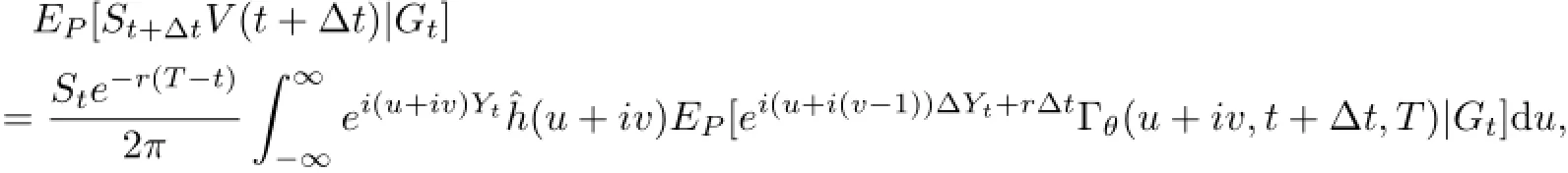
where ΔYt=Yt+Δt-Yt.Under the assumption Ut+Δt=Utfor small Δt,we have
Γθ(u+iv,t+Δt,T)=Γθ(u+iv,t,T)(1-Δt〈(diag(yPθ(u+iv))+A)Ut,1〉)+O(ΔT2). Thus we can obtain that
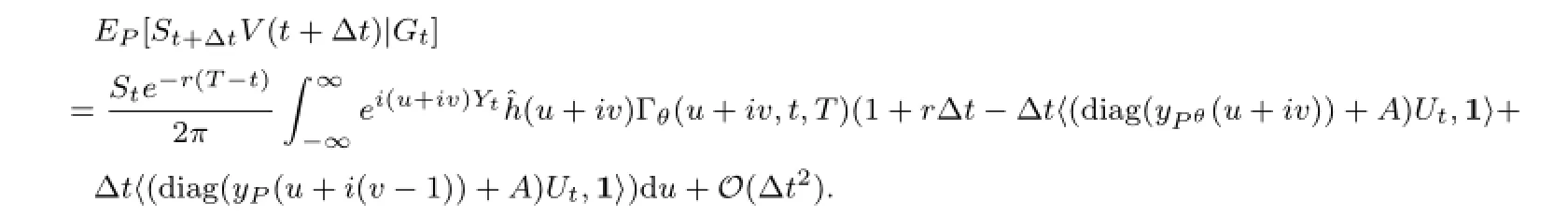
By the same argument,we obtain the second part that
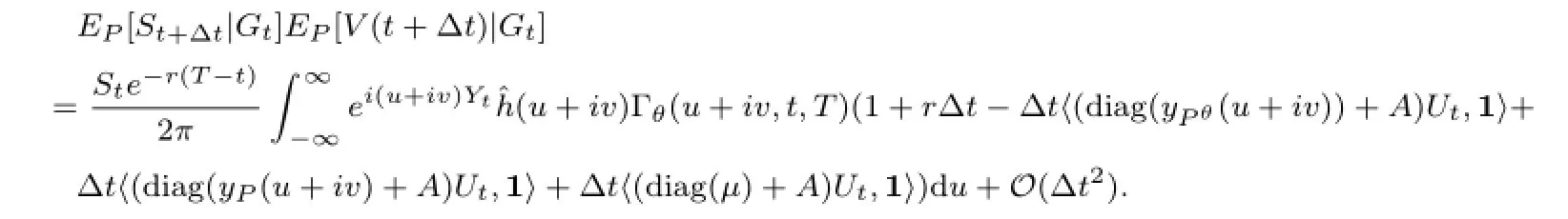
Therefore we obtain that
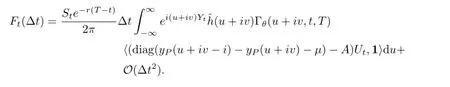
By the definition of yP,we have
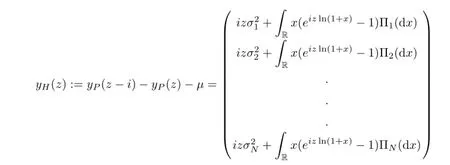
for z∈C.We obtain

Taking Δt→0,we obtain that
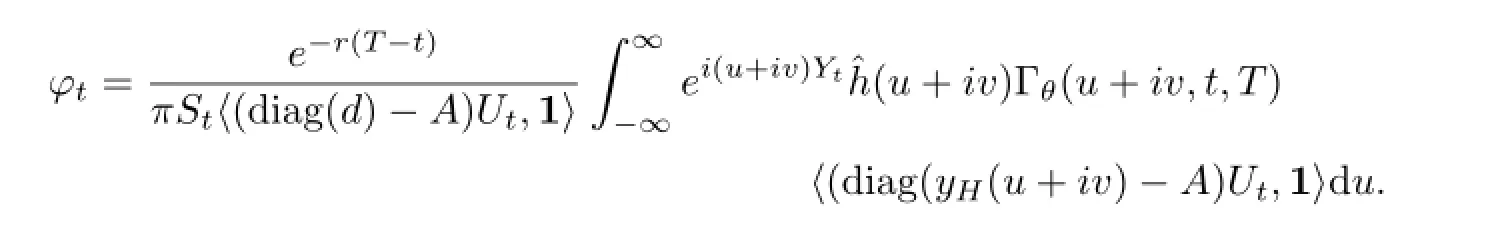
[1]ELLIOTT R J,AGGOUN L,MOORE J B.Hidden Markov Models:Estimation and Control[M].Berlin Heiderberg New York:Springer,1994.
[2]ELLIOTT R J,KOPP P E.Mathematics of Financial Markets[M].New York:Springer-Verlag,1999.
[3]BO Li-jun,WANG Yong-jin,YANG Xue-wei.Markov-modulated jump-diffusions for currency option pricing[J].Mathematics and Economics,2010,46:461-469.
[4]ELLIOTT R J,BUFFINGTON J.Regime switching and european options[J].Stochastic Theory and Control,2002,280:73-82.
[5]ELLIOTT R J,CHAN L,SIU T K.Option pricing and Esscher transform under regime switching[J].Annals of Finance,2005,1:423-432.
[6]GIUSEPPE D G,ROGERS L C G.Equity with Markov-modulated dividends[J].Quantitative Finance, 2009,9(1):19-26.
[7]SIU T K,YANG Hai-liang,JOHN W Lau.Pricing currency options under two-factor Markov-modulated stochastic volatility models[J].Insurance:Mathematics and Economics,2008,43:295-302.
[8]SONG Rui-li,WANG Bo.The MEMMs for Markov switching Lvy processes[J].Chinese Annals of Mathematics,2010,31A(5):549-556.
[9]CARR P,MADAN D.Option valuation using the fast fourier transform[J].Journal of Computational Finance,1999,2(4):61-73.
[10]KIM Y S,FABOZZI F J,LIN Zuo-dong,et al.Option pricing and hedging under a stochastic volatility Lvy process model[J].Review of Derivatives Research,2012,15(1):81-97.
[11]LEWIS A L.A simple option formula for general jump-diffusion and other exponential Lvy processes[J]. Ssrn Electronic Journal,2002,avaible from http://www.optioncity.net.
[12]LIU Rui-hua,ZHANG Qing,GEORGE YIN G.Option pricing in a regime switching model using the fast fourier transform[J].Journal of Applied Mathematics and Stochastic Analysis,2006,2006(3):1-22.
[13]BLACK F,SCHOLES M.The pricing of options and corporate liabilities[J].The Journal of Political Economy,1973,81(3):637-654.
[14]F¨OLLMER H,SCHWEIZER M.Hedging of contingent claims under incomplete information[J].Applied Stochastic Analysis,1990,5:389-414.
[15]BOYARCHENKO S I,LEVENDORSKII S Z.Non-Gaussian Merton-Black-Scholes Theory[M].Singapore: World Scientific,2002.
tion:60G51,60H05,94A17
:A
1002–0462(2017)01–0066–13
date:2015-11-11
Supported by the National Natural Science Foundation of China(11201221);Supported by the Natural Science Foundation of Jiangsu Province(BK2012468)
Biography:SONG Rui-li(1979-),female,native of Linyi,Shandong,an associate professor of Nanjing University of Finance and Economics,Ph.D.,engages in stochastic processes.
CLC number:O211.6
 Chinese Quarterly Journal of Mathematics2017年1期
Chinese Quarterly Journal of Mathematics2017年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- Bloch Constant on α-Bloch Mappings of the Unit Ball
- Solvable Lie Algebras with NilradicalTheir Casimir Invariants
- A Second Order Nonconforming Triangular Mixed Finite Element Scheme for the Stationary Navier-Stokes Equations
- The Translational Hull of Strongly Inverse Wrpp Semigroups
- Existence and Uniqueness of Solutions to Singular Higher Order Two-point BVPs on Time Scales
- Lvy-Prohorov Metric on the Measure Space
