WANG Zhi-jun,HAO Xiao-bin,SHI Dong-yang

(1.School of Mathematics and Statistics,Zhengzhou Normal University,Zhengzhou 450044,China; 2.School of Science,Henan Institute of Engineering,Zhengzhou 451191,China;3.School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450052,China)

A Second Order Nonconforming Triangular Mixed Finite Element Scheme for the Stationary Navier-Stokes Equations

WANG Zhi-jun1,HAO Xiao-bin2,SHI Dong-yang3

(1.School of Mathematics and Statistics,Zhengzhou Normal University,Zhengzhou 450044,China; 2.School of Science,Henan Institute of Engineering,Zhengzhou 451191,China;3.School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450052,China)

In this paper,a nonconforming triangular mixed finite element scheme with second order convergence behavior is proposed for the stationary Navier-Stokes equations. The new nonconforming triangular element is taken as approximation space for the velocity and the linear element for the pressure.The convergence analysis is presented and optimal error estimates of both broken H1-norm and L2-norm for velocity as well as the L2-norm for the pressure are derived.

stationary Navier-Stokes equations;nonconforming triangular mixed finite element scheme;optimal error estimates

§1.Introduction

We consider the following two-dimensional stationary Navier-Stokes equations

Problem(I)find u=(u1,u2)and p such that

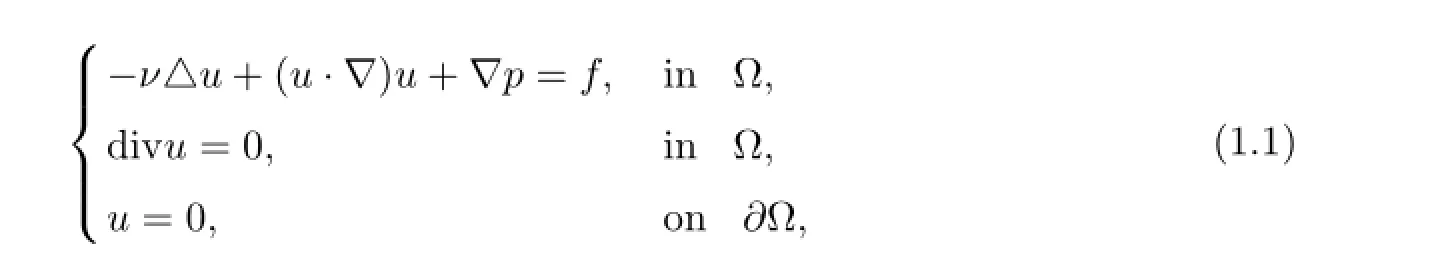
where ??R2is a bounded domain with boundary??,u denotes the fluid velocity vector field,p the pressure field,f=(f1,f2)the body force and ν＞0 the constant inverse Reynolds number.

The incompressible Navier-Stokes equations is one of the hot topics studied in mathematical physics and fluid mechanics fields(see[1-7]).For triangular conforming mixed finite schemes, it is well known that mini-element[8]has first order accuracy and P2-P1element[9]can yield second order accuracy.We are interested in nonconforming finite element methods for the stationary Navier-Stokes equations.Recently,these elements have attracted increasing attention from scientists and engineers in more wide areas for they have some practical advantages. On the one hand,they are usually much easier to be constructed to satisfy the discrete infsup condition than the conforming ones,which is usually required in the mixed finite element analysis.On the other hand,from the domain decomposition method point of view,the use of nonconforming finite elements with the degrees of freedom defined on the element edges and the element itself facilitates the exchange of information across each subdomain and provides spectral radius estimates for the iterative domain decomposition operator[10]since the unknowns are associated with the element edges,each degree of freedom belongs to at most two elements. In[11],Crouzeix and Raviart considered the nonconforming finite element approximations to the stationary incompressible Stokes equations.Their low-order,nonconforming simplicity elements consist of standard nonconforming P1simplicity elements for velocity and piecewise constants for the pressure.They showed that this combination is stable and can yield first order accuracy.Based on the two-level discretizations and multiscale finite element method[12]discussed two kinds of finite element algorithms for steady Navier-Stokes equation.On the other hand,the stabilized nonconforming finite element method is presented for the transient Naiver-Stokes equation in[13]and a low order mixed finite element method is studied in[14]for nonstationary incompressible Navier-Stokes equations,the superconvergent error estimates of the velocity in the broken H1-norm and the pressure in the L2-norm are obtained,respectively. However,it seems that there are few studies focusing on the approximations to problem(1.1) with triangular nonconforming finite element methods which can lead to second order accuracy.

In this paper,we consider the discretization of the stationary Navier-Stokes equations in two-dimensional domain by a new nonconforming mixed finite element scheme with second order convergence behavior,in which a new triangular nonconforming element is constructed and used as approximation space for the velocity,and piecewise linear element for the pressure. The convergence analysis is presented and the error estimates are obtained.

An outline of the paper is as follows.In section 2,we introduce the variational formulation for problem(I)and the existence and uniqueness of its solution.In section 3,we will state the construction of the new triangular nonconforming mixed finite element scheme.In section 4,we prove that the pair of mixed finite element spaces satisfy the discrete inf-sup condition.The convergence analysis is presented and error estimates both of the velocity in the broken H1-norm and of the pressure in the L2-norm are obtained by use of the element’s special properties. In the last section,we use the duality argument to derive error estimate in the L2-norm for the velocity.

We denote by Wk,p(?)(Wk,p(?)2)the standard Sobolev space of k-differential functions in Lp(?)(Lp(?)2),its norm by‖·‖k,p,?,and the norm of Hk(?)(Hk(?)2)by‖·‖k,?. When k=0,we let L2(?)(L2(?)2)denote the corresponding space defined on ? with norm‖·‖0.Throughout the paper,C indicates a positive constant,possibly different at different occurrences,which is independent of the mesh parameter h,but may depend on ? and other parameters introduced in this paper.Notations not especially explained are used with their usual meanings.

§2.Construction of the Nonconforming Mixed Finite Element Scheme

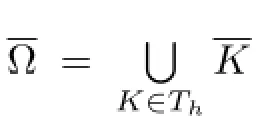
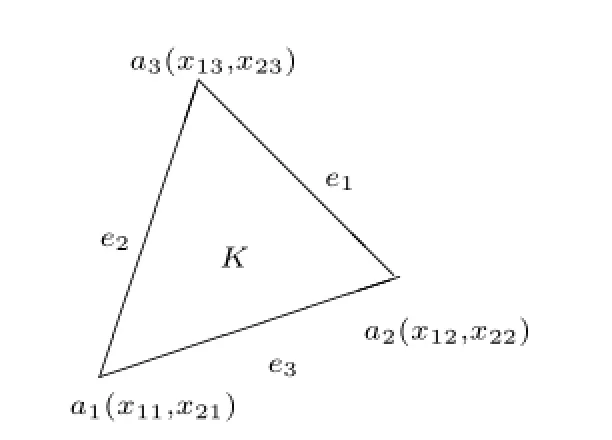
Fig.1the elementK

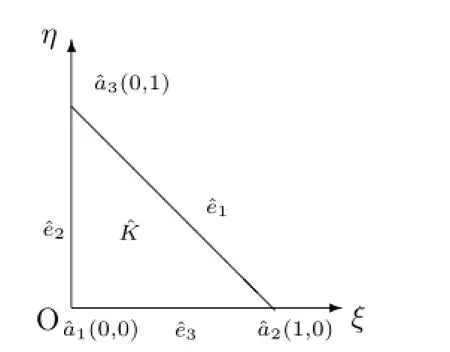
Fig.2the reference element?K

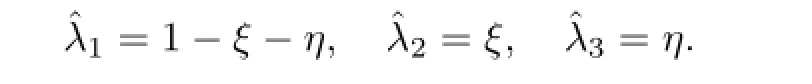
and

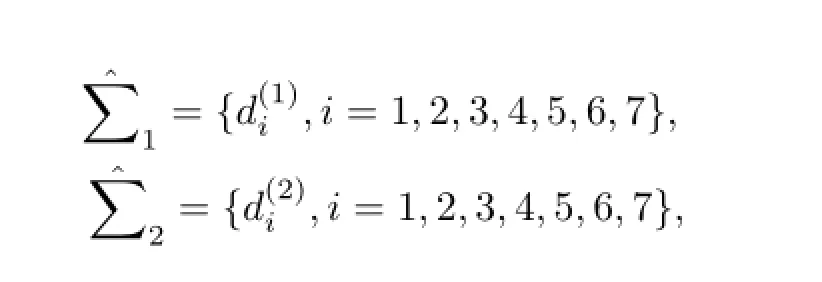
respectively.Where

respectively.Where

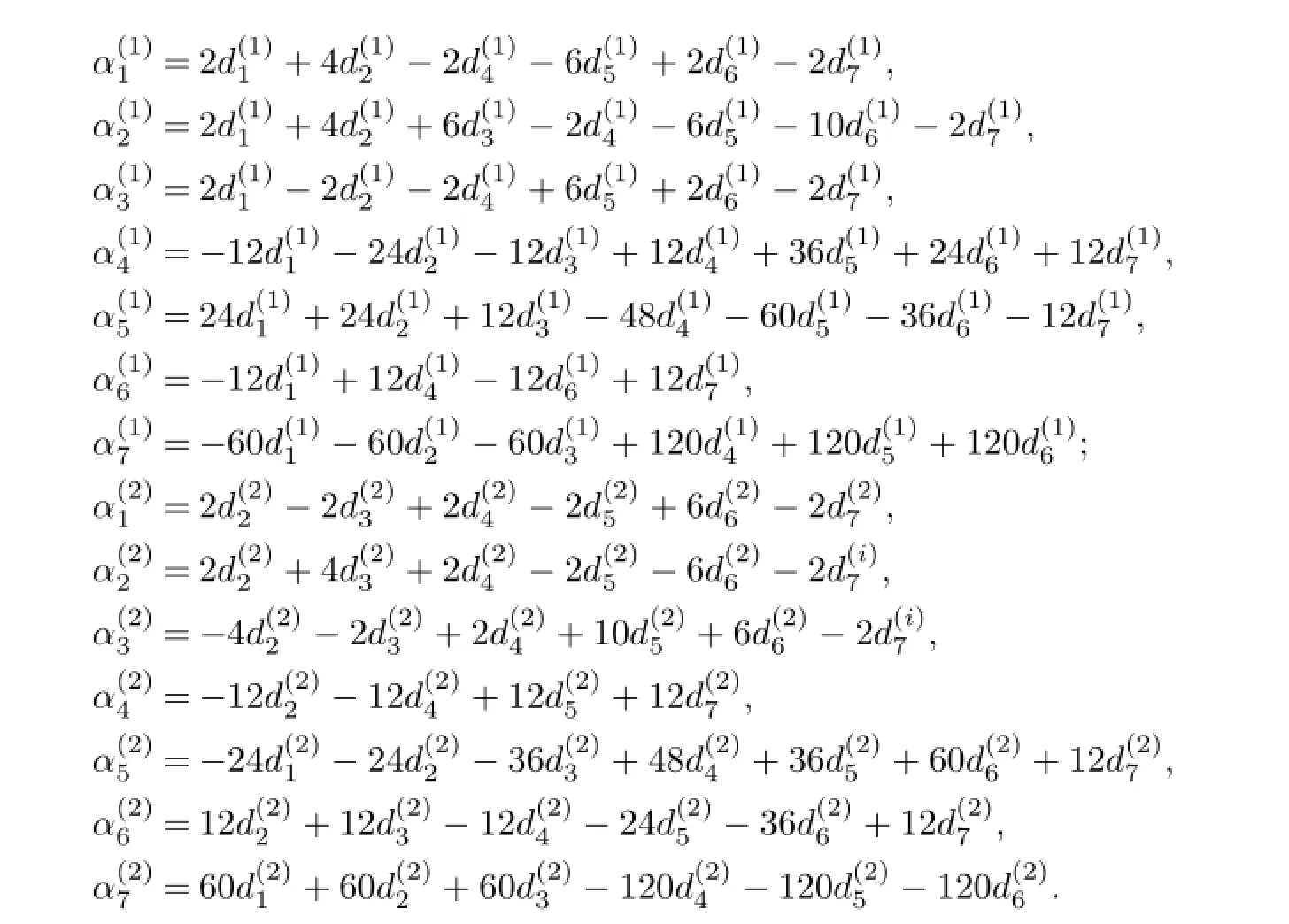
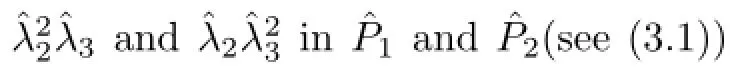
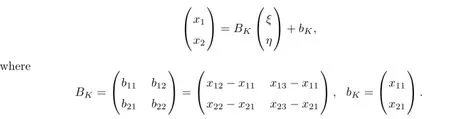
Then the associated finite element spaces Xhand Mhcan be defined as

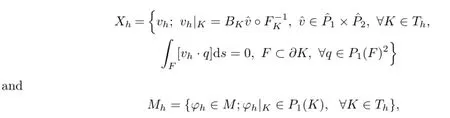
where[vh·q]stands for the jump of vh·q across the edge F if F is an internal edge and it is equal to vh·q itself if F belongs to??,P1(K)and P1(F)denote the sets of first polynomials on K and F,respectively.

Obviously,Xh/?H1(?)2,Mh?M,so this is a nonconforming mixed finite element scheme.

Let Πhbe the associated interpolation operator over Xn.

For all vh=(v1h,v2h)∈Xh,we define

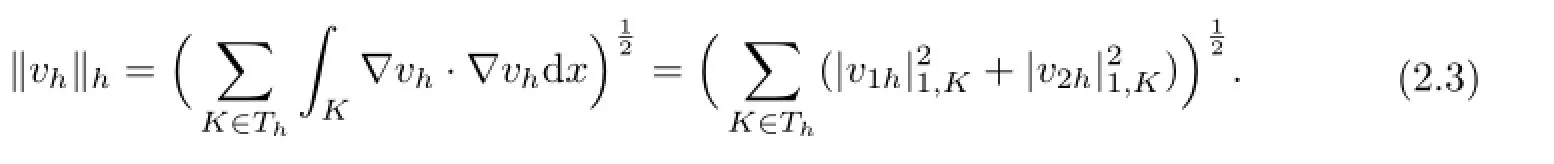
Then‖·‖his a norm over Xh.

§3.The Existence and Uniqueness of the Approximated Solution

The variational formulation for the Problem(I)is written as Problem(I?)Find(u,p)∈X×M,such that

From[4,6]we know that the Problem(I?)has at least a solution(u,p)∈X×M.

We introduce the bilinear ah(·,·),bh(·,·)and trilinear ah1(·;·,·)forms as

and?uh,vh,wh∈Xh,

The approximation of the Problem(I?)reads as follows:

Problem(Ih)Find(uh,ph)∈Xh×Mh,such that

For the bilinear ah(·,·),bh(·,·)and trilinear ah1(·;·,·),they have the following properties(see [4,6,13-17]),?uh,vh,wh∈Xh,ph∈Mh,

With the similar argument as[3]we can show the following discrete embedding inequality over Xh

Using(3.8),we can prove that there exists a positive number N0＞1,such that

Therefore

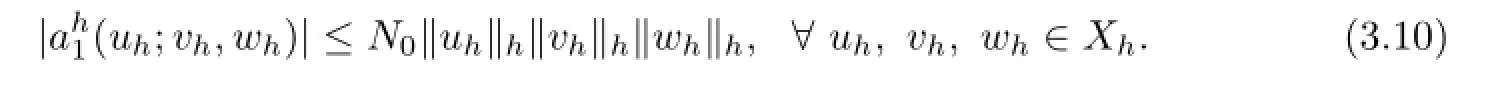
Next we discuss the existence and uniqueness of the solution of the Problem(Ih).In order to do this,we first prove the following Lemma.

Lemma 4.1The spaces Xhand Mhsatisfy inf-sup condition(see[17]),i.e.,

where β is a positive constant independent of h.

ProofOn the one hand,since Πhis invariant to piecewise constant,applying interpolation theory,we have

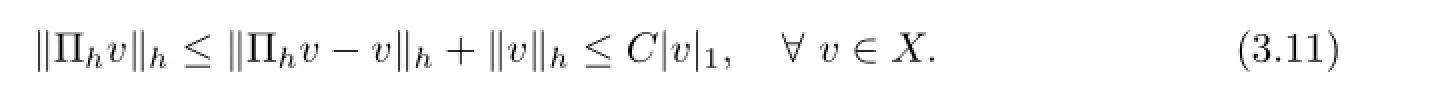
On the other hand,by the definition of interpolation Πhand Green’s formula,?v∈X

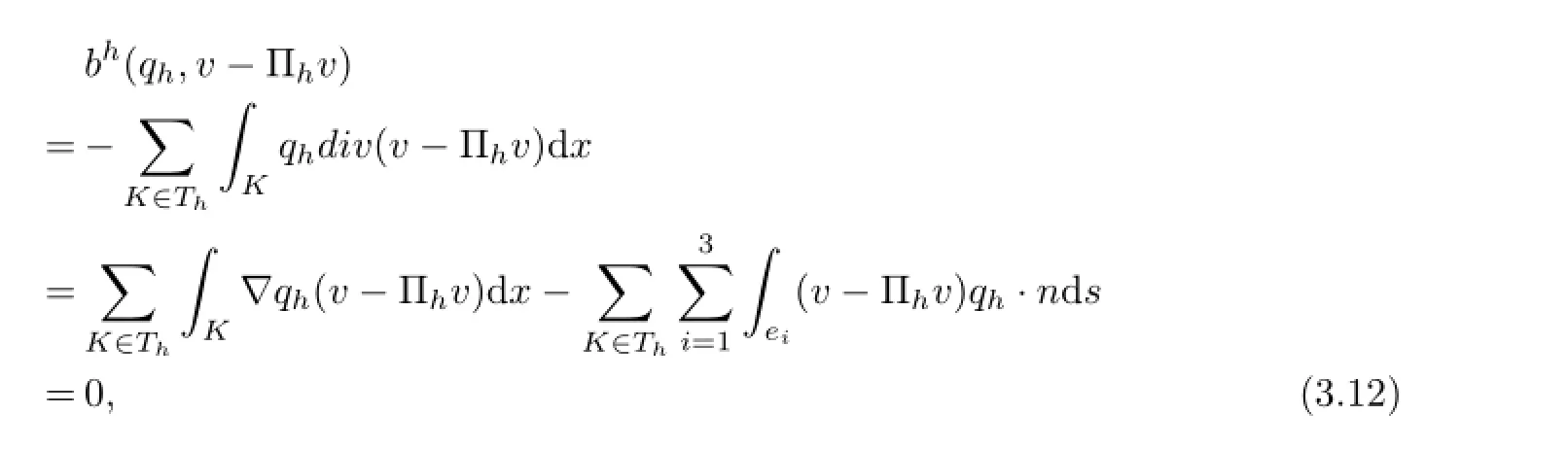
here and later n denotes the unit normal vector to ei.

Since the pair X and M satisfy inf-sup condition(see[19]),there exists a constant β0＞0 such that

Therefore,we have

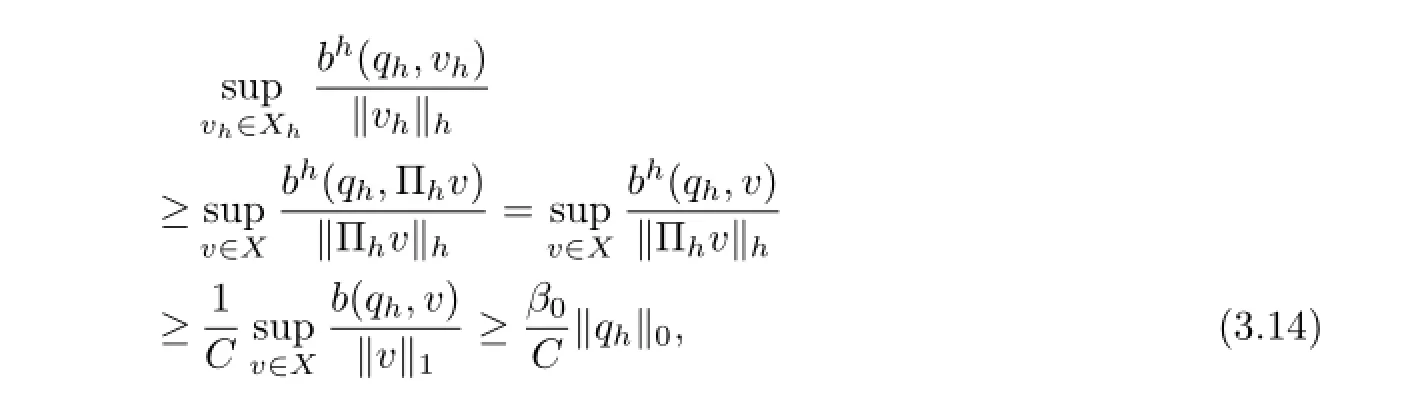
Using the similar way to[3,15]we can obtain the following conclusion.

Theorem 3.1Let(u,p)∈X×M is the solution to the Problem(I)and let

Then the Problem(Ih)has a unique solution(uh,ph)∈Xh×Mhsatisfying

§4.The Error Estimates

In order to derive the error estimates,we need the following important lemmas.

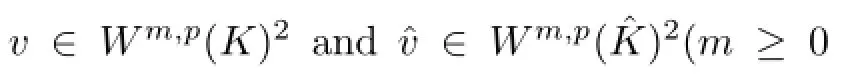
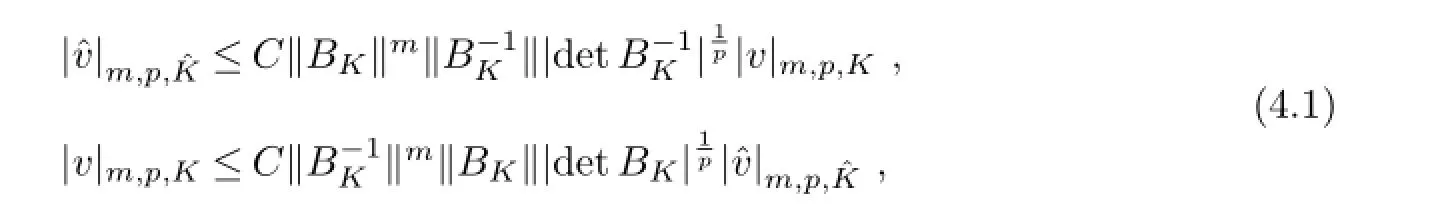
where‖·‖is Euclid norm of matrix BK.

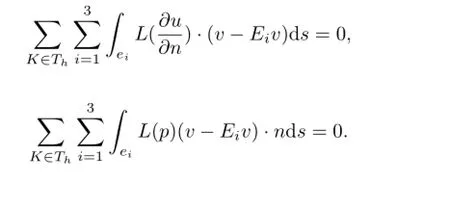
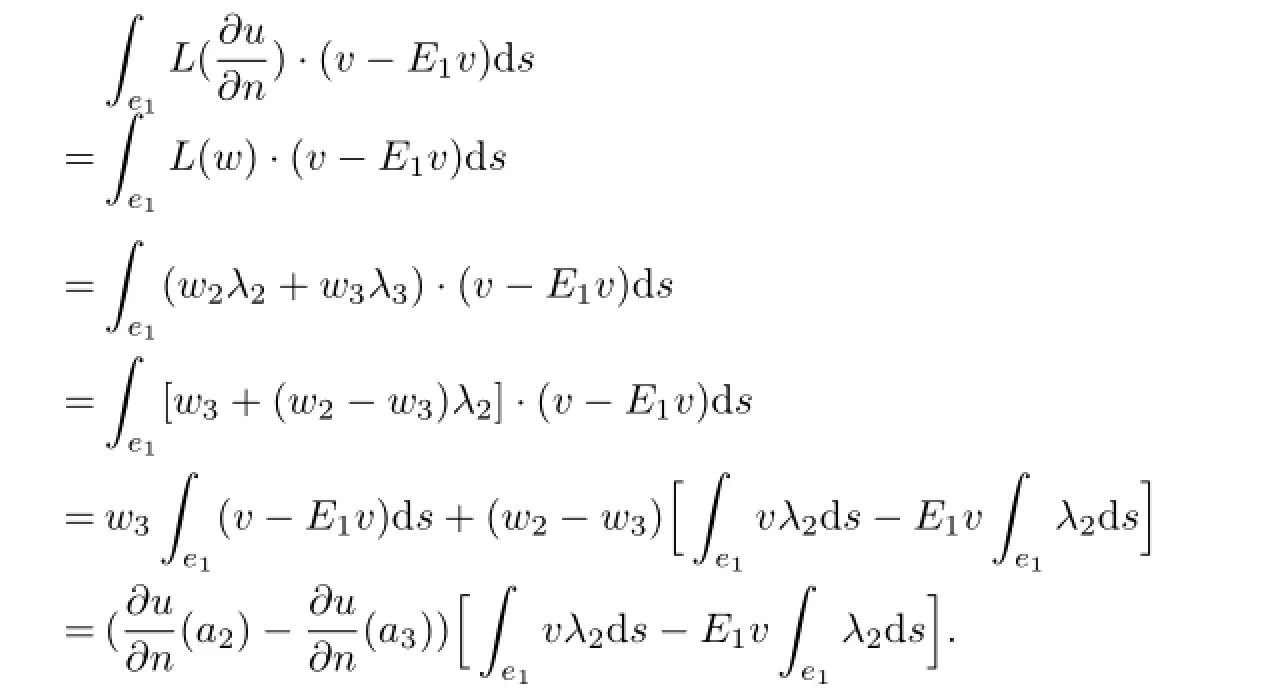
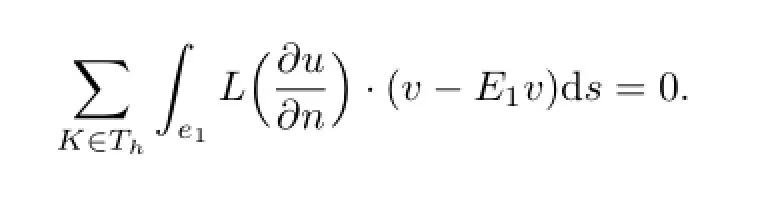
Similarly,we have

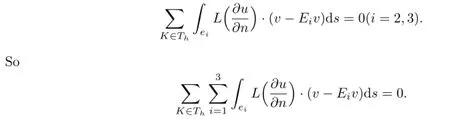
Similarly,

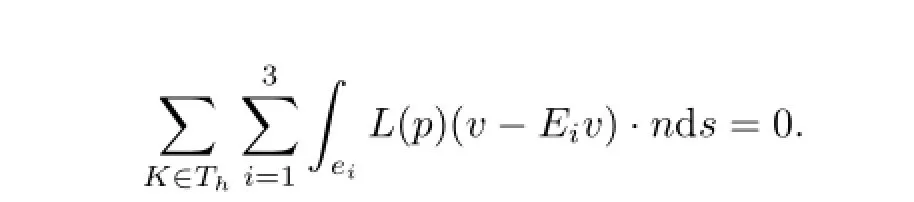
This completes the proof.

Lemma 4.4 Assume that u∈H3(?)2and p∈H2(?).Then for all v∈Xh∪H10(?)2, we have

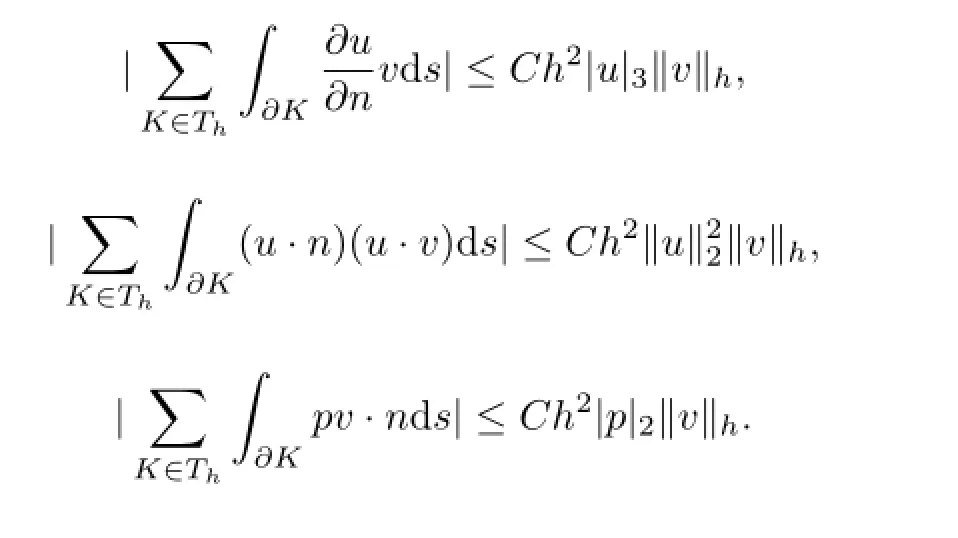
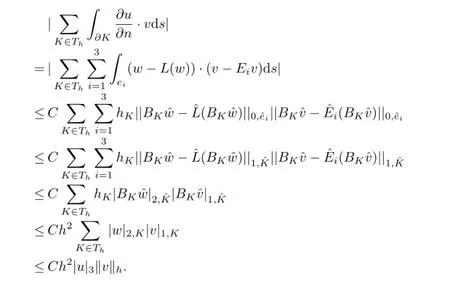
Similarly,we can get

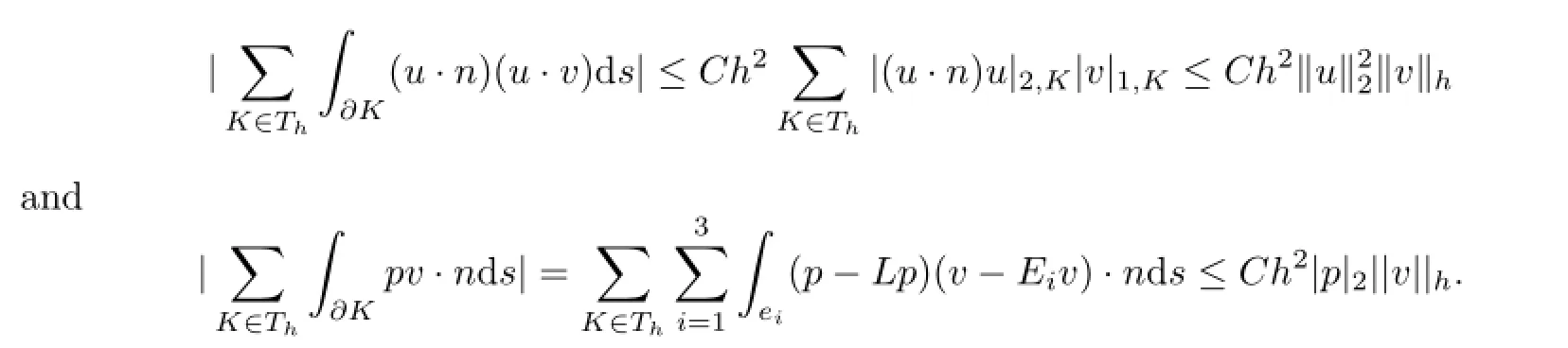
The proof is completed.

Theorem 4.1Let(u,p)∈(X∩H3(?)2)×(M∩H2(?)),(uh,ph)∈Xh×Mhbe the solutions to the Problem(I?)and the Problem(Ih),respectively,then we have

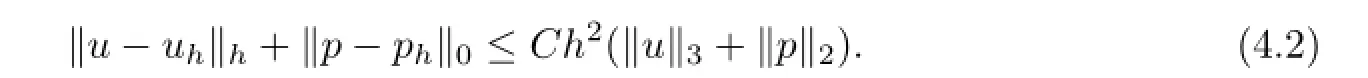
ProofUsing a similar argument as in[15],we can obtain the result.

Then using the duality argument introduced by Aubin and Nitsche,we can establish the error estimate in L2-norm for the velocity(see[17]for details).

Theorem 4.2Let(u,p)∈(X∩H3(?)2)×(M∩H2(?)),(uh,ph)∈Xh×Mhbe the solutions of the Problem(I?)and the Problem(Ih),respectively,then there holds

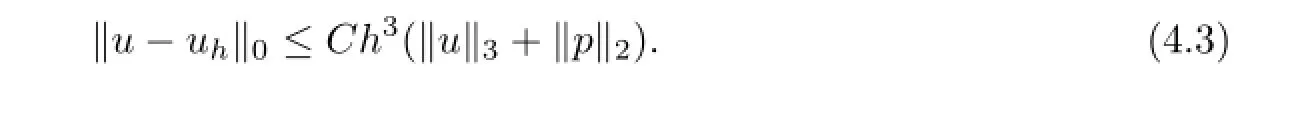
[1]NICOLAIDES R A.Analysis and convergence of the MAC scheme II:Navier-Stokes equations[J].SIAM J Numer Anal,1992,65:29-44.

[2]SHI Dong-yang,REN Jin-cheng,GONG Wei.A new nonconforming mixed finite element scheme for the stationary Navier-Stokes equations[J].Acta Mathematica Scientia,2011,31(2):367-382.

[3]SHI Dong-yang,REN Jin-cheng.Nonconforming mixed finite element approximation to the stationary Navier-Stokes equations on anisotropic meshes[J].Nonlinear Analysis:Theory Methods Applications,2009, 71(9):3842-3852.

[4]GIRAULT V,RAVIART P A.Finite Element Method for Navier-Stokes Equations:Theory and Algorithms[M].New York:Springer-Verlag,1986.

[5]SHI Dong-yang,GONG Wei,REN Jin-cheng.A new stable second order nonconforming mixed finite element scheme for the stationary Stokes and Navier-Stokes equations[J].Mathematical and Computer Modelling, 2011,53(9-10):1956-1969.

[6]TEMAM R.Navier-Stokes Equation,Theory and Numerical Analysis[M].New York:North-Hoolland Amsterdam,1984.

[7]THOMASSET F.Implementation of Finite Element Methods for Navier-Stokes Equations[M].Berlin:Springer,1981.

[8]ARNOLD D N,BREZZI F,FORTIN M.A stable finite element for the Stokes equations[J].CALCOLO, 1984,21:337-344.

[9]HOOD P,TAYLOR C.Navier-Stokes Equations Using Mixed Interpolation[M].Alabama:University of Alabama in Huntsville(UAH)Press,1974:121-132.

[11]CROUZEIX M,RAVIART P A.Conforming and nonconforming finite element methods for solving the stationary Stokes equations[J].RAIRO Numer Anal,1973,7:33-76.

[12]WEN Juan,HE Yin-nian,WANG Xue-min,et al.Two-level multiscale finite element methods for the steady Navier-Stokes problem[J].Acta Mathematica Scientia,2014,34(3):960-972.

[13]XIE Chun-mei,FENG Min-fu.New nonconforming finite element method for solving transient Navier-Stokes equations[J].Applied Mathematics and Mechanics,2014,35(2):237-258.

[14]XU Chao.SHI Dong-yang.LIAO Xin.Low order nonconforming mixed finite element method for nonstationary incompressible Navier-Stokes equations[J].Applied Mathematics and Mechanics,2016,37(8): 1095-1112.

[15]SHI Dong-yang,REN Jin-cheng.A new second order nonconforming mixed finite element scheme for the stationary Stokes and Navier-Stokes equations[J].Applied Mathematics and Computation,2009,207(2): 462-477.

[16]LI Kai-tai,ZHOU Lei.Finite element nonlinear Galerkin methods for penalty Navier-Stokes equations[J]. Math Numer Sinica,1995,17:360-380.

[17]CIARLET P G.The Finite Element Method for Elliptic Problems[M].New York:North-Hoolland Amstedam,1978.

[18]ADAMS R A.Sobolev Spaces[M].New York:Academic Press,1975.

[19]LI Kai-tai,HUANG Ai-xiang.The Finite Element Methods and Applications(II)[M].Xi’an:Xi’an Jiaotong University Press,1987(in Chinese).

tion:65N30,65N15

:A

1002–0462(2017)01–0088–11

date:2016-10-23

Supported by the National Natural Science Foundation of China(11271340,116713697); Supported by Henan Natural Science Foundation of China(132300410376)

Biographies:WANG Zhi-jun(1969-),male,native of Xingyang,Henan,an associate professor of Zhengzhou Normal University,engages in finite element method and application;HAO Xiao-bin(1974-),male,native of Pingdingshan,Henan,a lecturer of Henan Institute of Engineering,engages in finite element method and application;SHI Dong-yang(1961-),male,native of Lushan,Henan,a professor of Zhengzhou University,engages in finite element method and application.

CLC number:O242.21