孫愛慧

(吉林師范大學數學學院,吉林四平136000)

上三角矩陣代數上的Jordan 全可導點

孫愛慧

(吉林師范大學數學學院,吉林四平136000)

Zhao和Zhu證明了如下結果：復數域上的任意上三角矩陣代數中的每一矩陣都是Jordan全可導點.本文將證明：特征不為2的無限域上的任意上三角矩陣代數中的每一矩陣都是Jordan全可導點.

Jordan全可導點;導子;上三角矩陣代數;三角代數

0 引言

設R為一個有單位元的交換環(huán),A為R上的一個代數.我們總是用1A表示A中的單位元,令X°Y=X Y+YX,設n≥2為一個固定的整數.

設φ:A→A是一個R-線性映射.若對任意的X,Y∈A,都有φ(X°Y)=φ(X)° Y+X°φ(Y)成立,則稱φ是一個導子.設G∈A.若對任意的X,Y∈A,且X Y=G,有φ(X°Y)=φ(X)°Y+X°φ(Y)成立,則稱φ在G點Jordan可導.如果每一個在G點Jordan可導的線性映射都是一個導子,則稱G是一個Jordan全可導點(見文獻［1］).

Zhao和Zhu在文獻［1］中應用算子代數的方法證明了如下結果：復數域上的任意上三角矩陣代數的每一個元素都是全可導點.本文將使用代數方法證明：特征不為2的無限域上的任意上三角矩陣代數中的每一矩陣都是Jordan全可導點.

1 主要結論

定理特征不為2的無限域上的任意上三角矩陣代數中的每一矩陣都是Jordan全可導點.

在證明定理之前,我們需要如下引理：

引理［2］設F是一個無限域,Τn(F)是F上的一個n×n上三角矩陣代數.設φ是Τn(F)上的一個F-線性映射.假設對于任意的可逆元X∈Τn(F)有φ(X)=0,則φ=0.

證明假設對于任意的可逆陣X∈Τn(F)有φ(X)=0.任取A∈Τn(F),由于F是無限域,則存在λ∈F,使得λ1Τn(F)-A是可逆的.由假設我們有φ(λ1Τn(F)-A)=0,以及φ(1Τn(F))=0,因此φ=0.證畢.

下面我們給出定理的證明.

定理證明設F是一個特征不為2的無限域,Τn(F)是F上的一個n×n的上三角矩陣代數,又設G∈Τn(F),假定φ:Τn(F)→Τn(F)是一個Jordan可導的F-線性映射.我們的目標是證明φ是一個導子.

設A=Τr(F),M=Mr,t(F),B=Τt(F),此處r+t=n,則Τn(F)可看成一個三角代數(關于三角代數的定義及性質,參見文獻［3-5］).設,令

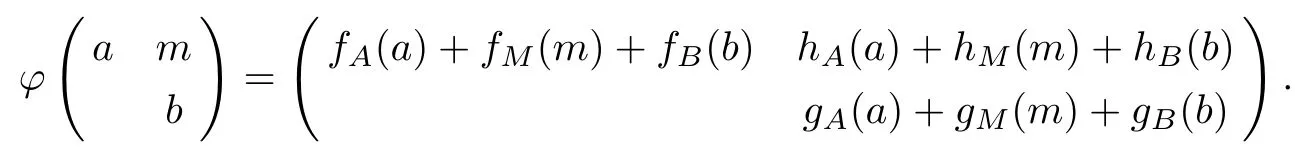
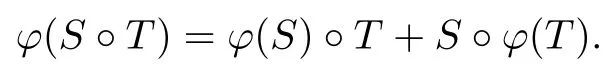
由上式兩邊展開后得：

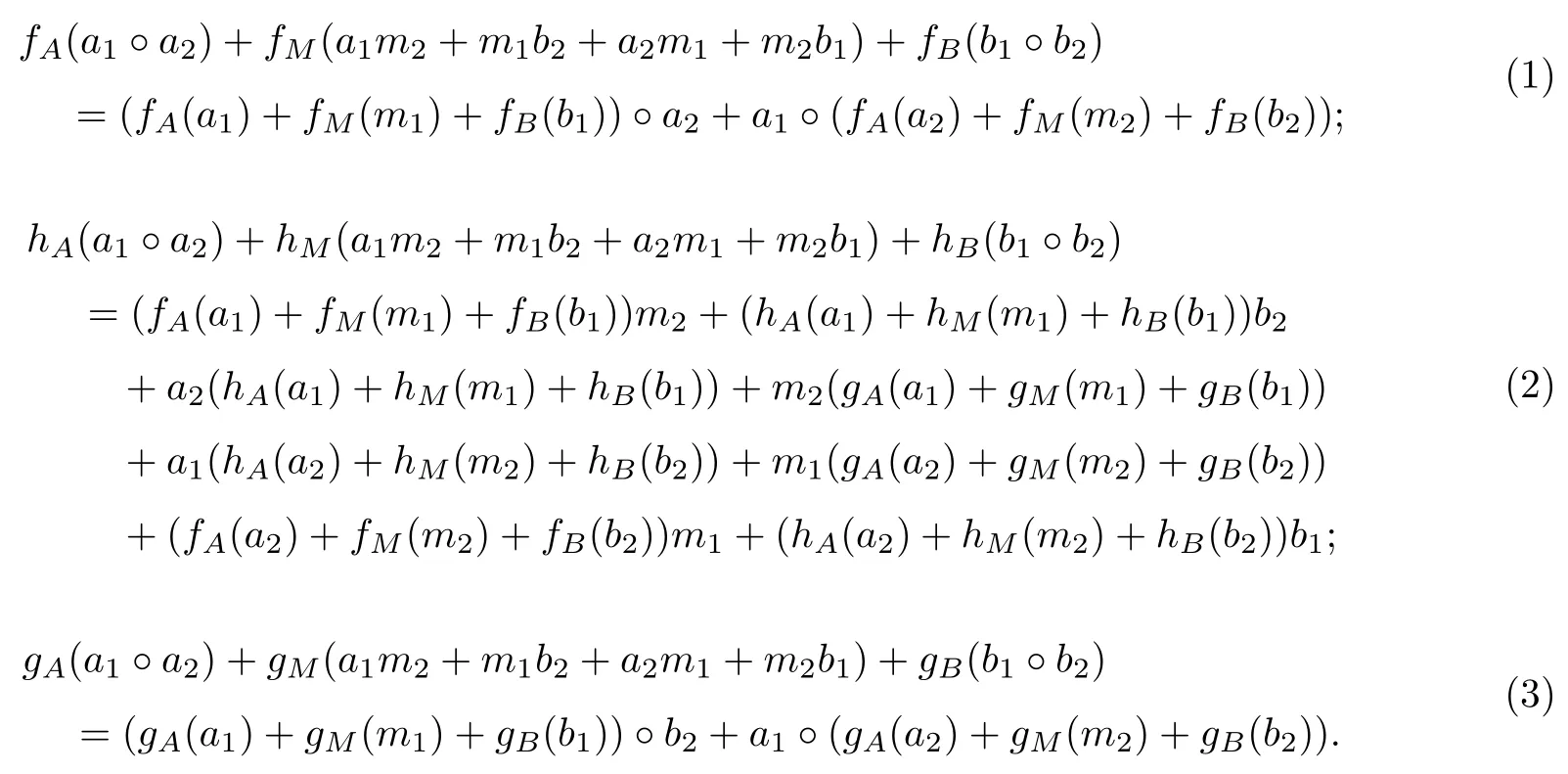
我們分五步來證明:

第一步將證明:fM=0=fB,gA=0=gM.

對于任意的m∈M以及非零的λ∈F,在(1)式中取a1=λ1A,m1=m0-λm,b1=b0, a2=λ-1a0,m2=m,b2=1B,則有

由于F是一個無限域,則由上面的等式得到:對于任意的m∈M有2fM(m)+ 2fB(1B)=0.易見fM(m)=0,從而fM=0.

對任意的可逆元b∈B,以及非零的λ∈F,在(1)式中取a1=1A,m1=0,b1=λb0b-1, a2=a0,m2=m0,b2=λ-1b,則有

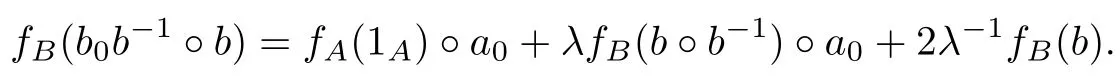
由于F是一個無限域,則由上面的等式得到:2fB(b)=0,從而fB(b)=0.由引理可知fB=0.類似地,由(3)式可得gA=0=gM.

第二步我們證明:hA=0=hB.

對任意的可逆元a∈A以及非零的λ∈F,在(2)式中取a1=a,m1=λm0,b1=λb0, a2=a-1a0,m2=0,b2=λ-11B,并利用關系hB(1B)=0,可得

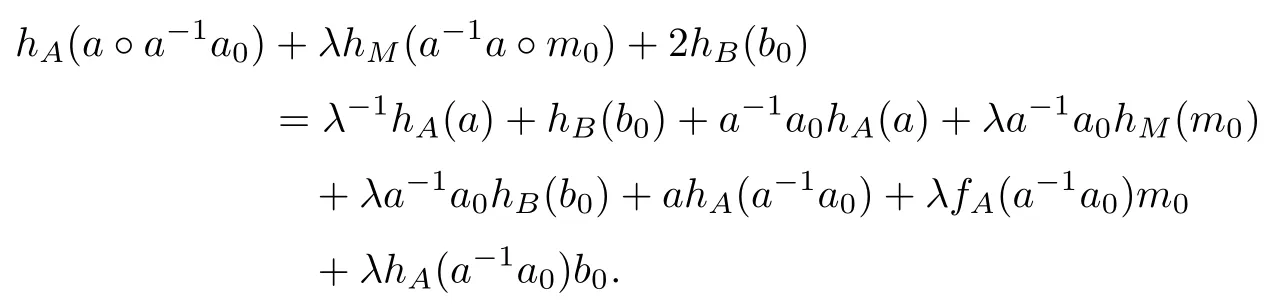
由于F是一個無限域,由上面的等式可得hA(a)=0.再由引理可得hA=0.類似地,由(2)式可得hB=0.

第三步將證明:對于任意的a∈A,m∈M,b∈B,有

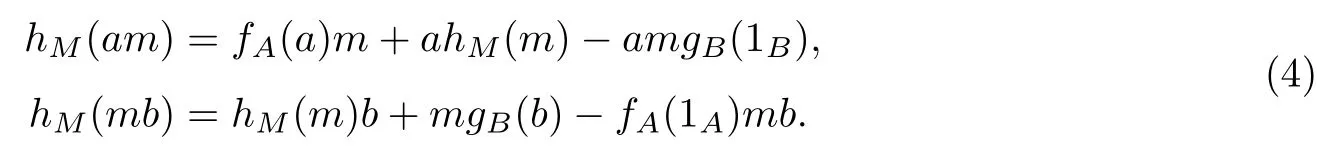
對任意的可逆元b∈B,m∈M以及非零的λ∈F,在(2)式中取a1=1A,m1=m, b1=λ-1b0b-1,a2=a0,m2=m0-λm b,b2=λb,可得

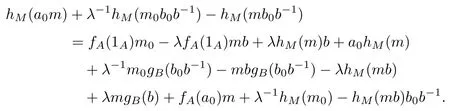
由于F是一個無限域,由上面的等式可得：

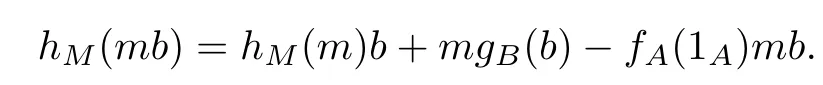
再由引理可知等式(4)成立.

第四步將證明：對于任意的a∈A,m∈M,b∈B,都有

首先假設G/=0.由(4)式可見只需證明fA(1A)=0=gB(1B).在(4)式中令a=1A,則對于任意的m∈M,有fA(1A)m=m gB(1B).根據文獻［3,Proposition 3］可得

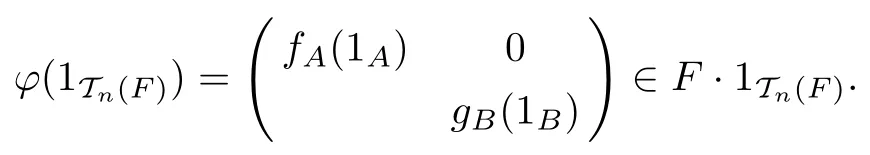
另一方面,由于φ在G點Jordan可導,并且1Τn(F)G=G,則有

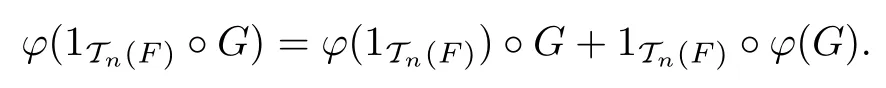
因此,φ(1Τn(F))°G=0.又由F的特征不為2,可得φ(1Τn(F))G=0.考慮G/=0可得φ(1Τn(F))=0.即fA(1A)=0=gB(1B).

第五步最后證明fA與gB均為導子.

利用第四步的結果可見,對于任意的a1,a2∈A,m∈M有

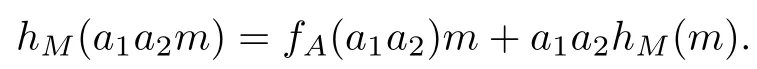
另一方面,對于任意的a1,a2∈A,m∈M,都有

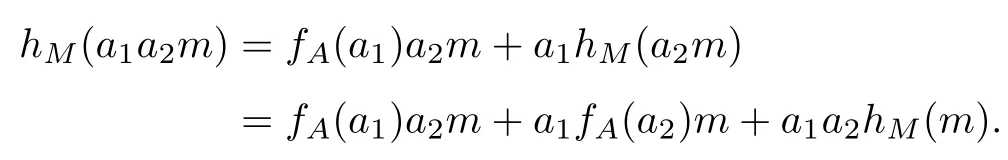
由上述兩個等式可得,對于任意的a1,a2∈A,有

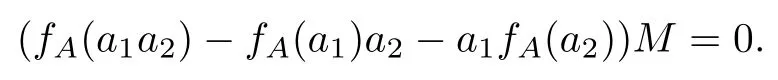
由于M是一個左忠實A-模,可得fA(a1a2)-fA(a1)a2-a1fA(a2)=0,即fA為導子.同理可得gB也為導子.綜合上述步驟,由［4,引理5］可得φ是一個導子.

［1］ZHAO S,ZHU J.Jordan all-derivable points in the algebra of all upper triangular matrices［J］.Linear Algebra Appl,2010,433:1922-1938.

［2］ZHU J. Characterization of all-derivable points in nest algebras ［J］. proc Amer Math Soc, 2013, 141: 2343-2350.

［3］CHEUNG W S. Commuting maps of triangular algebras ［J］. J London Math Soc, 2001, 63(1): 117-127.

［4］CHEUNG W S. Lie derivations of triangular algebras ［J］. Linear and Multilinear Algebra, 2003, 51(3): 299-310.

［5］梁才學,朱軍,趙金平.三角代數上的廣義Jordan高階導子［J］.杭州電子科技大學學報,2011,31(2):82-85.

(責任編輯林磊)

Jordan all-derivable points in upper triangular matrix algebras

SUN Ai-hui
(College of Mathematics,Jilin Normal University,Siping Jilin 136000,China)

Zhao and Zhu proved the following result:Every matrix in upper triangular matrix algebras over the com p lex number field is a Jordan all-derivable point.The aim of this paper is to show that every matrix in upper triangular matrix algebras over an in finite field of characteristic not 2 is a Jordan all-derivable point.

Jordan all-derivable point;derivation;upper triangular matrix algebra; triangular algebra

O 153.3

A

10.3969/j.issn.1000-5641.2016.01.005

1000-5641(2016)01-0039-04

2014-11

國家自然科學基金(11301215);吉林省科技廳青年科研基金(20130522094H)

孫愛慧,女,碩士,副教授,研究方向為基礎數學.E-mail:sunaihui2002@126.com.