LIJing-jing,LIU Juan

(College of Mathematics Sciences,Xinjiang Normal University, Urumqi 830054,China)

Bi-super-connected digraphs

LIJing-jing,LIU Juan

(College of Mathematics Sciences,Xinjiang Normal University, Urumqi 830054,China)

A simple digraph D(without loops and multiple arcs)is said to be super connected if every minimum vertex-cut is the out-neighbor set or in-neighbor set of a vertex. A super-connected digraph D is said to be bi-super-connected if there exists a minimum vertex-cut is both the out-neighbor set of a vertex and the in-neighbor set of a vertex. In this paper,we will give the necessary and sufficient conditions of line digraph is bisuper-connected,furthermore,we study the bi-super-connectivity of Cartesian product and lexicographic product of two digraphs.

combinatorial problem s;super-connected;bi-super-connected;line digraphs;Cartesian product

0 Introduction

Let D=(V(D),A(D))be a sim p le digraph.The connectivity κ(D)is the minimum cardinality of all Vertex-cuts of digraph D.It is well know that κ(D)≤δ(D),whereδ(D)=m in{δ+(D),δ-(D)}is the minimum degree of D(δ+(D)andδ-(D)are the minimum out degree and the minimum in-degree).Hence,a digraph D is said to be maximally connected ifκ(D)=δ(D).A strongly connected digraph D is said to be super-connected,or super-κfor short,if there exists a Vertex x such that U=N+(x)or N-(x)for any minimum Vertex-cut U,where N+(x)and N-(x)are out-neighbor set and in-neighbor set of a Vertex x in D.If d+(x)=d-(x)=d for each Vertex x∈V,then D isa d-regular digraph.denotes a directed cycle of length of n.denotes a complete digraph of order n.The reverse digraph of D is the digraph D(r)=(V,{(x,y)|(y,x)∈A}),D is a symmetric digraph if A=A(r).The line digraph of D,denoted by L(D),is the digraph With Vertex set V(L(D))={aij|aij=(xi,xj)∈A(D)}, and a Vertex aijis adjacent to a Vertex astin L(D)if and only if xj=xsin D.

Let D1=(V1,A1)and D2=(V2,A2)be two digraphs,where V1={x1,x2,···,xn1}and V2={y1,y2,···,yn2}.The Cartesian product D1□D2of D1and D2has Vertex set V1×V2and((x1,y1),(x2,y2))∈A(D1□D2)if and only if either(x1,x2)∈A1and y1=y2,or x1=x2and(y1,y2)∈A2.The lexicographic product D1［D2］of D1and D2has Vertex set V1×V2and ((x1,y1),(x2,y2))∈A(D1［D2］)if and only if either(x1,x2)∈A1,or x1=x2and(y1,y2)∈A2. Let S1,S2,···,Sn1-1and Sn1be n1digraphs.The digraph D1［S1,S2,···,Sn1］is the digraph obtained from D1by replacing the i th Vertex of D1by a copy of the digraph Si,in such a way that for every arc(xi,xj)in D1,D1［S1,S2,···,Sn1］contains all possible arcs from V(Si)to V(Sj).In［1］,the authors introduced the definition of bi-super-connected,in this paper,we study the bi-super-connectivity of line digraph,Cartesian product and lexicographic product of two digraphs.

Definition 1［1］A super-connected digraph D is said to be bi-super-connected,i?there exist a minimum vertex-cut U such that U=N+(x)=N-(y)?or x,y∈V(D).

Bi-super-connected digraphs are super-connected and super-connected symmetric digraphs are bi-super-connected.If D is a bi-super-connected digraph,thenδ+(D)=δ-(D).

The study on connectivity of the Cartesian product can be found in［2-3］,where the lower bounds of the connectivity of two graphs and some sufficient conditions for it to be maximally or super-connected are giVen.In［4-6］,the authors discussed the connectivity of line graphs(digraphs).Shieh［7］determined the super-connected and super-edge-connected Cartesian product of two regular graphs.Liu and Meng［8］searched the super-connected and super-arc-connected Cartesian product of digraphs.In［9］,the authors studied the double-super-connected of line digraph and Cartesian product and lexicographic product of two digraphs.In this paper,we w ill giVe the necessary and sufficient conditions of line digraph is bi-super-connected,furthermore,we study the bi-super-connectivity of Cartesian product and lexicographic product of two digraphs.

1 Operations on digraphs

Firstly,we giVe the characterization of the bi-super-connected line digraphs.

Lemma 2［10］Let D be a digraph,thenλ(D)=κ(L(D)).

Theorem 3 Let D=(V,A)be a simple digraph,then L(D)is bi-super-connected i?andonly i?λ(D)=1 and there exists a cut-arc(xi,xj)∈A satisfies that d+(xi)=d-(xj)=1 in D.

P roof Ifλ(D)=1,thenκ(L(D))=1 by Lemma 2.There is a cut-Vertex aijin L(D), aij=(xi,xj)∈A(D)is a cut-arc in D,if it satisfies that d+(xi)=d-(xj)=1,then there exist two Vertices asi=(xs,xi),ajt=(xj,xt)∈V(L(D))such that N+(asi)=N-(ajt)={aij}in L(D).Therefore,L(D)is bi-super-connected.

On the other hand,let L(D)be bi-super-connected and there exists a minimum Vertex-cut U of L(D).Thus,there exist two Vertices asi=(xs,xi),ajt=(xj,xt)∈V(L(D))such that N+(asi)=U=N-(ajt).By the definition of line digraph,we known that there are|U|parallel arcs from xito xjin D.Since D is sim ple,we have|U|=1.Thusκ(L(D))=1.Therefore, λ(D)=1 by Lemma 2.Iffor any cut-arc(xi,xj)∈A(D),then there is no Vertex asisuch that N+(asi)={aij}or Vertex ajtsuch that N+(ajt)={aij},a contradiction.

Next,we characterize the bi-super-connected Cartesian product D1□D2of two digraphs D1and D2.In the following of this section,we w ill assume thatδ(D)=δ+(D)=δ-(D)for digraph D.For conVenience,we use the symbols ni,δi,κito denote the order,them inimum degree and the connectivity of digraph Di,for i=1,2.

By the definition of“bi-super-connected”,we known that if D1□D2is super-κ and there exists a minimum Vertex-cut U of D1□D2such that U=N+((x,y))=N-((x,y)),(x,y)∈V(D1□D2),then D1□D2is bi-super-connected.Thus,in the following theorem,we will consider that there exists a minimum Vertex-cut U of D1□D2such that U=N+((x,y))=N-((x,y)) does not hold for any Vertex(x,y)∈V(D1□D2).

The following theorem in［8］forκi=δi=1 is useful in our proof.

Theorem 4［8］Let D1and D2be two simple strongly connected digraphs and let?or i=1,2.I?δi=κi,then D1□D2is super-κi?and only i?,whereκ(D)=δ(D)=1,n≥2.

Therefore,ifκi=δi=1 for i=1,2,then D1□D2is super-κif and only if

Theorem 5 Let D1and D2be two strongly connected digraphs,then D1□D2is bi-superconnected i?and only i?the?ollowing conditions hold:

i)κi=δi=1?or i=1,2,

iii)There exists a vertex x∈Viwith d+(x)=1 such that,and a vertex x∈Viwith d-(x)=1 such that?or i=1,2.

P roo f If i)and ii)hold,then D1□D2is super-κby Theorem 4 and there exists Vertex (x,y)∈V(D1□D2)such that U=N+((x,y))for each minimum Vertex-cut U.By i)and iii), U=N+((x,y))={(x,y1),(x1,y)}=N-((x1,y1))thus D1□D2is bi-super-connected.

On the other hand,if D1□D2is bi-super-connected,then D1□D2is super-κ.We first prove i).Without loss of generality,suppose thatδ1≥2.We assume that U is a minimum Vertex-cut of D1□D2.Since D1□D2is bi-super-connected,thus there are two Vertices(x,y)and(x′,y′)((x,y)/=(x′,y′))With N+((x,y))=U=N-((x′,y′)).Set,,then

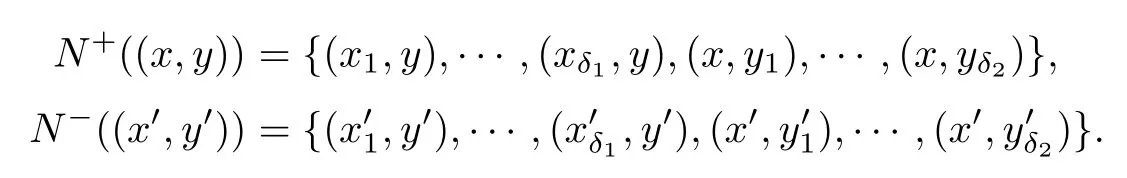
Sinceδ1≥2 andδ2≥1,thus N+((x,y))/=N-((x′,y′)),a contradiction,i)holds.By Theorem 4,if i)holds and D1□D2is super-κ,then ii)holds.Finally,we prove iii).Without loss of generality,suppose that for any Vertex x∈V1With d+(x)=1 such thatwhereThere is a Vertex y∈V2With d+(y)=1,let,then U=N+((x,y))={(x′,y),(x,y′)}?N-((x′,y′))is a minimum Vertex-cut of D1□D2,and there is no(x′′,y′′)∈V(D1□D2)such that U=N-((x′′,y′′)),a contradiction.

Lemma 6［9］Let D=(V,A)be a strongly connected d-regular digraph.I?there exists a vertex y∈V such that?or any vertex-cut,then D is a symmetric digraph.

Theorem 7 Let D1and D2be two strongly connected regular digraphs.Then D1□D2is bi-super-connected i? and only i? one o? the ?ollowing conditions holds:

i)D1and D2are symmetric digraphs and D1□D2is super-κ.

ii)D1and D2are directed cycles except?or(k≥3),wheredenote the directed cycle o?length k.

P roo f If i)holds,D1□D2is super-κthen there is a Vertex(x.y)∈V(D1□D2)such that N+((x,y))=U for any minimum Vertex-cut.D1and D2are symmetric digraph, so N+((x,y))=U=N-((x,y)).Thus,D1□D2is bi-super-connected.If ii)holds,then D1□D2is bi-super-connected by Theorem 5.

On the other hand,if D1□D2is bi-super-connected,then D1□D2is super-κ,we consider two cases:

Case 1 If there exists a minimum Vertex-cut U of D1□D2such that U=N+((x,y))= N-((x,y)),(x,y)∈V(D1□D2),then there exists a Vertex x∈Visuch that U′=N+(x)= N-(x)for any Vertex-cut U′=N+(z)(or N-(z))of Difor i=1,2.By Lemma 6,D1and D2are symmetric digraphs,i)holds.

Case 2 If for any Vertex(x,y)∈V(D1□D2)such that U=N+((x,y))=N-((x,y)) for any minimum Vertex-cut U of D1□D2does not hold,thenδ1=δ2=1 by Theorem 5.Since D1and D2are strongly connected regular digraphs,we have,D1and D2are directed cycles, ii)holds.□

Finally,we characterize the bi-super-connected lexicographic product of two digraphs.

It is clear that if D1is an isolated Vertex,then D1［D2］D2,and if D2is an isolated Vertex,then D1［D2］D1.In the following,we always assume that D1and D2are strongly connected digraph With at least two Vertices.

Theorem 9［9］D1［D2］is super-κi?and only i?D1is a complete digraph and D2is super-κ.

Theorem 10 D1［D2］is bi-super-connected i?and only i?D1is a complete digraph and D2is bi-super-connected.

P roof If D1［D2］is bi-super-connected,then D1［D2］is super-κ,wehaVe D1isa com p lete digraph and D2is super-κby Theorem 9.ObVious D2is bi-super-connected.

On the other hand,if D2is bi-super-connected,then D2is super-κ.Since D1is a complete digraph,so we have D1［D2］is super-κby Theorem 9.The Vertex setis the out-neighbor and in-neighbor of,and D2is bi-super-connected,thus,D1［D2］is bi-super connected.

［1］MENG J X, ZHANG Z. Super-connected arc-transitive digraphs ［J］. Discrete Applied Mathematics, 2009, 157:653-658.

［2］CHIUE W S, SHIEH B S. On connectivity of the Cartesian product of two graphs ［J］. Applied Mathematics and Computation, 1999, 102: 129-137.

［3］XU J M, YANG C. Connectivity of Cartesian product graphs ［J］. Discrete Mathematics, 2006, 306: 159-165.

［4］MENG J X. Superconnectivity and super edge-connectivity of line graphs ［J］. Graph Theory Notes of New York,XL 2001: 12-14.

［5］XU J M, LV M, MA M J, HElLLWIG A. Super connectivity of line graphs ［J］. Information processing Letters,2005, 94: 191-195.

［6］ZHANG Z, LIU F X, MENG J X. Super-connected n-th interated line digraphs ［J］. OR Transanctions, 2005, 9:35-39.

［7］SHIEH B S. Super edge- and point-connectivities of the Cartesian product of regular graphs ［J］. Networks, 2002,40: 91-96.

［8］LIU J, MENG J X. Super-connected and super-arc-connected Cartesian product of digraphs ［J］. Information processing Letters, 2008, 108: 90-93.

［9］LIU J, MENG J X, ZHANG Z. Double-super-connected digraph ［J］. Discrete Applied Mathematics, 2010, 158:1012-1016.

［10］XU J M. Topological Structure and Analysis of Interconnection Networks ［M］. Dordrecht, Netherlands: Kluwer Academic publishers, 2001.

(責(zé)任編輯李藝)

有向圖的雙超連通性

李靜靜,劉娟
(新疆師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,烏魯木齊830054)

簡單有向圖D(無環(huán)與重弧),如果滿足每個最小點割都是某個點的出鄰點集或入鄰點集,則稱D是超連通的.在超連通有向圖D中,如果存在一個最小點割既是某個點的出鄰點集又是某個點的入鄰點集,則稱D是雙超連通的.主要研究了線圖雙超連通性的充要條件;同時,研究了笛卡爾積與字典積的雙超連通性.

組合問題;超連通;雙超連通性;線圖;笛卡爾積

2015-01

國家自然科學(xué)基金(61363020,11301450);新疆維吾爾自治區(qū)青年科技創(chuàng)新人才培養(yǎng)工程(2013731011);新疆維吾爾自治區(qū)自然科學(xué)基金(2012211B21);新疆研究生科技創(chuàng)新項目(2014118)

李靜靜,女,碩士研究生,研究方向為圖論與組合數(shù)學(xué).E-mail:804474119@qq.com.

劉娟,女,教授,研究方向為圖論與組合數(shù)學(xué).E-mail:liu juan1999@126.com.

O 157 Document code:A

10.3969/j.issn.1000-5641.2016.01.011

1000-5641(2016)01-0091-05