Quantum Measurement of Two-Qubit System in Damping Noise Environment?
Qing Yang(楊青), Hui Liu(劉),Xiu-Lan Zhen(甄秀蘭),Ming Yang(揚(yáng)名), and Zhuo-Liang Cao(曹卓良)
1Key Laboratory of Opto-electronic Information Acquisition and Manipulation,Ministry of Education,School of Physics&Material Science,Anhui University,Hefei 230601,China
2School of Electronic and Information Engineering,Hefei Normal University,Hefei 230061,China
1 Introduction
As one of the most striking features in quantum theory,quantum entanglement is the essential resource for quantum information processing.[1?3]But entanglement degradation through unwanted coupling with the environment remains a major obstacle.It is significant to study the entanglement under the influence of environment. Mathematically,quantum entanglement means that the state of a quantum system cannot be expressed as the form of product state or the convex sum of product states.The entanglement of two qubits can be measured by concurrence.[4]However,entanglement is not the only aspect of quantum correlations.The nonlocality and nonclassical correlation have close relations to the entanglement,although they are substantially different in concepts.If an arbitrary quantum state is nonlocal,it is also entangled.[5]But the converse is not true:there exist mixed entangled states that satisfy local hidden variable description.[5?6]The nonlocality is usually measured by the extent of the quantum-mechanical violation of Bell’s inequality.As regards for nonclassical correlation,it is measured by quantum discord(QD).[7]For pure states,quantum discord reduces exactly to a measure of entanglement,namely the entropy of entanglement.But for mixed state,there is no clear relation between QD and entanglement.In essence,there is not a specific boundary on understanding of the above three measurements.So it is desirable to investigate quantum correlations from different perspective.
More researchers devote themselves to investigation of the dynamics of quantum correlation for a given initial two-qubit entangled state in various environments.[8?17]For example,Konrad et al.proved a general factorization law for two-qubit systems,which describes the entanglement evolution on passage of either component through an arbitrary noisy channel.[18]And they illustrated that the maximally entangled state would retain its role in the evolution of entanglement under one-side noisy channnel.Furthermore,Farias et al.experimentally demonstrated the residual entanglement is proportional to the initial entanglement in the case of one-side noise.[19]Recently,Wang et al.investigated the decoherence of two-qubit entangled states in the local two-sided amplitude-damping noise and showed us that there exist a set of partially entangled states that are more robust than maximally entangled states in terms of the residual quantum correlation measured by concurrence,fully entangled fraction and quantum discord,respectively.[20]This interesting and counterintuitive phenomenon inspires us to study further on the evolution of quantum correlations of two-qubit system under ADC and GADC by using concurrence,QD and Bell-inequality.
This paper is organized as follows:In Sec.2,the model in the local ADC is introduced.The evolutions of concurrence,QD and Bell-nonlocality of the bipartite system are investigated.In Sec.3,we investigate the evolutions of different quantum correlations under GADC.In Sec.4,a conclusion of our work is given.
2 ADC Model
Amplitude damping noise exists in many practical qubit systems with the loss of energy,such as atomic qubit with spontaneous decay.In this paper,we consider the effect of amplitude-damping environment on quantum correlations of two qubits.
The decoherence can be described in the language of quantum channels.[21]Let ε be a quantum channel that maps the input state ρinonto the output state ρout.It is known that the action of ε can be characterized by a set of operators called Kraus operators.[22]For any initial two-qubit state,the action of an amplitude-damping environment ε can be described as:
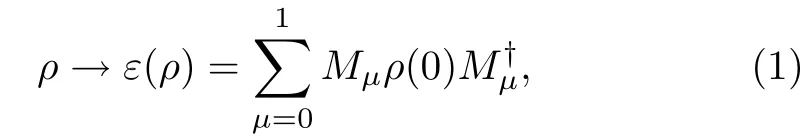
where Mμare Kraus operators satisfyingM0and M1are defined by:
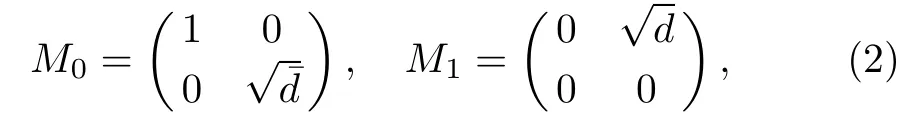
where d denotes the decoherence strength of the qubit in the noise environment.0 6 d 6 1 andˉd=1?d.Note that d=0 denotes the noise-free case and d=1 means the interaction time or strength between the system and the environment tending to infinity.Therefore,the decoherence strength d is acquiesced in the range(0,1)in the following discussion.
Assume that the two qubits are initially in an entangled state:

with 0 6 u 6 1,=1?u.
In the computational basis{|00i,|01i,|10i,|11i},the matrix of the initial state ρ0is given by:

Considering that one of the qubits is transmitted and undergoes an ADC,then we have the degraded density matrix ρ1as:

For the convenience of calculation and analysis,we assume the strengths of the decohenrence on each qubit are the same when considering that each qubit undergoes the ADC.Then we have the density matrix ρ2as:
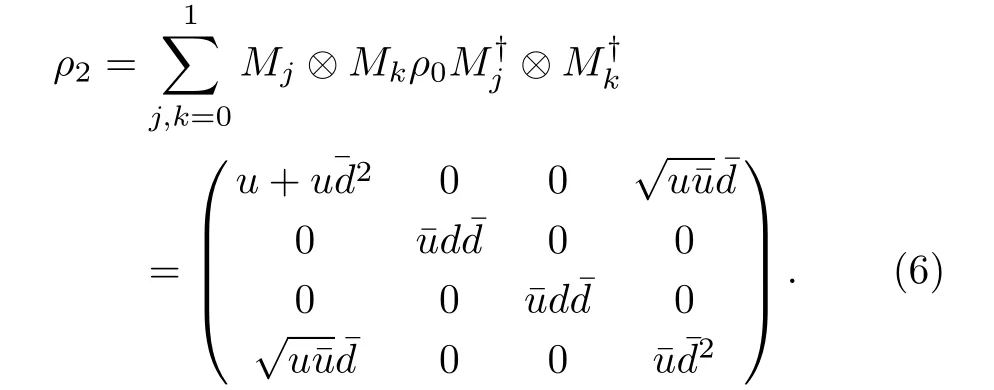
Obviously,the states ρ1and ρ2are dependent on the parameters d and u.
In order to investigate the evolution of quantum correlation of the bipartite system,we choose three typical measurements:Concurrence,quantum discord,and nonlocality.Concurrence is a convenient normalized measurement to determine the degree of entanglement,and widely accepted for any two-qubit case.Quantum discord is defined as a difference between quantum mutual information and classical correlation[7]in a bipartite system.It is a kind of quantum correlation that may include entanglement but is an independent measure.Bell-nonlocality is measured by the extent of the quantum-mechanical violation of Bell-inequalities.Nonlocality and entanglement are substantially different in concepts,but they are closely related.We present three different kinds of results as to the above measurements under the influence of one-side noise and two-side noise.
2.1 Concurrence
Firstly we measure the entanglement of|Ψi straightforwardly by concurrence.The corresponding concurrence for the two-qubit state ρ is given by C(ρ)=where the ξiare the eigenvalues of the matrix ρ·?ρ in decreasing order with?ρ=(σy?σyρ?σy?σy)and ρ?the complex conjugation of ρ,σythe conventional Pauli matrix.The concurrence of the initial state can be easily computed:It’s obvious that C(|Ψi)reaches the maximum value at u=1/2 indicating that|Ψi is a maximally entangled state.
The concurrence of ρ1and ρ2can be easily computed:

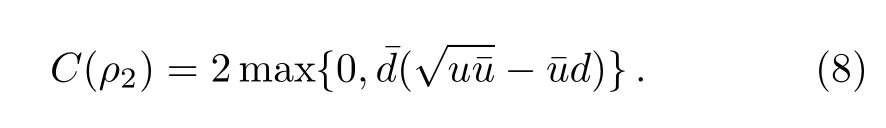
The concurrence evolution C(ρ1)and C(ρ2)with u in a given d are shown in Fig.1.It can be seen from Fig.1(a)that the maximum value of C(ρ1)is achieved at u=1/2 and reduces with the increasement of decoherence strength d.The result is monotonic with respect to that of|Ψi in case of one-side noise.
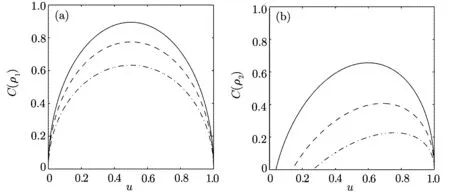
Fig.1 The concurrence C(ρ1)and C(ρ2)versus the parameter u for a given decoherence strength d.The solid and blue line:d=0.2;The dashed and green line:d=0.4;The dotted and red line:d=0.6.
The maximum value of C(ρ2)is:
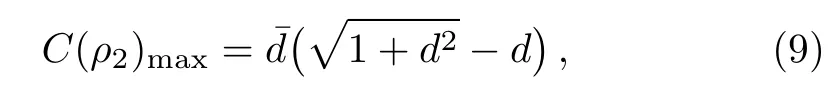
with

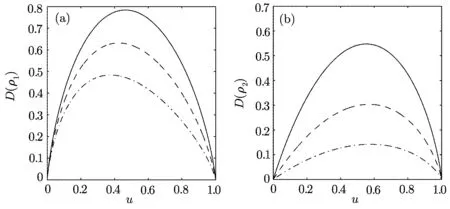
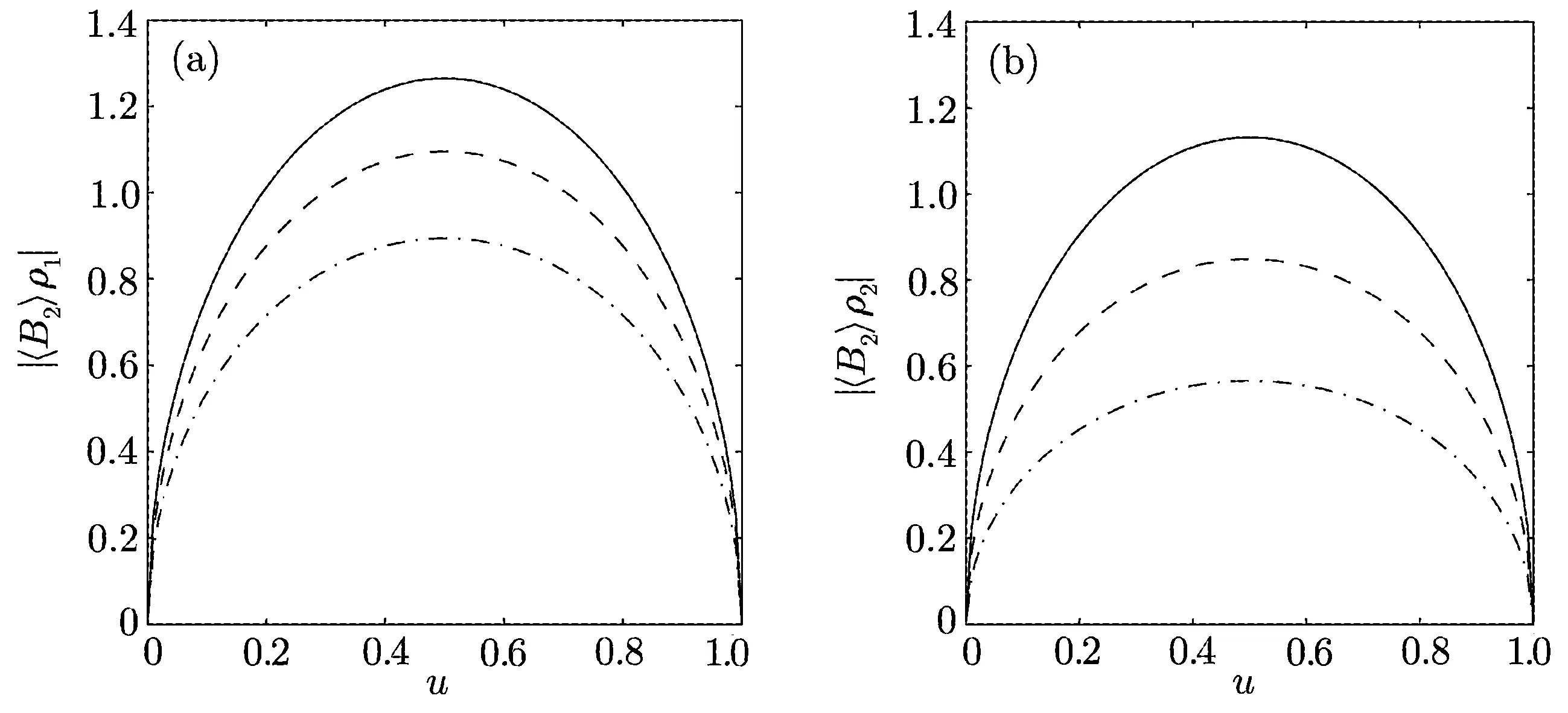
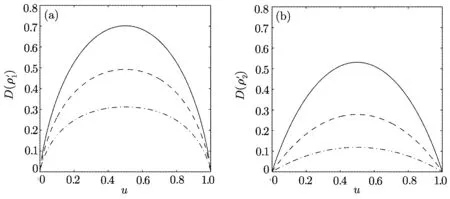
Figure 1(b)shows that C) QD is a measurement of the discrepancy between two natural yet different quantum analogs of the classical mutual information.It is fundamentally different from the various entanglement measures.Thus we investigate QD of the decoherence state ρ1and ρ2. For a given quantum state ρABof a composite bipartite system AB,the quantum mutual information is given by: where S(ρ)= ?Tr(ρlog2ρ)is the von Neumann entropy.ρA(ρB)is the reduced density matrix of subsystem A(B).Moreover,I(ρAB)was shown that quantum mutual information is the maximum amount of information that A(lice)can send securely to B(ob)if a composite correlated quantum state is used as the key for a one-time pad cryptographic system.[23]The classical correlation can be expressed by JA(ρAB)=S(ρB)? minwhere the minimum is taken over all possible positive operator valued measures(POVMs)or von Neumann measurements{}on subsystem A with pk=Tr(ρAB)and ρB|k=TrA(ρAB)/pk.QD is simply obtained by subtracing the classical correlations from the quantum mutual information:[7] The obstacle to computing QD lies in this complicated maximization procedure for calculating classical correlation,because it is difficult to find the optimal measurement for minimizing PkpkS(ρB|k). Fortunately,the state ρ0, ρ1, ρ2all belong to a particular case of X-states.[24]The density matrix of a twoqubit X-states in the representation spanned by two-qubit product states|1i=|0iA?|0iB,|2i=|0iA?|1iB,|3i=|1iA?|0iB,|4i=|1iA?|1iBis of the general form Recently,an underlying symmetry structure of these states has been examined.[25]The quantum state ρXsatisfies the unit trace and positive conditionsP=1,ρ22ρ33>|ρ23|2and ρ11ρ44>|ρ14|2. After a straightforward calculation[26]we obtain the QD of states ρ0is As for state ρ1, where For state ρ2, where Fig.2 Quantum discord D(ρ1)and D(ρ2)versus the parameter u.The solid and blue line:d=0.2;The dashed and green line:d=0.4;The dotted and red line:d=0.6. As shown in Fig.2,we can see that both in the case of one-side noise and two-side noise,the consequence of QD are not proportional to that of the initial state.In case of the one-side noise QD reaches the maximum value at um<1/2.While in two-side niose,QD reaches its maximum value when um>1/2.That is to say,we can not get the maximum value of QD at u=1/2 both in condition of the one-side noise and the two-side noise acting on the initial state. The evolution of Bell nonlocality has attracted much attention.[27?29]The Bell-nonlocality of the quantum state in case of bipartite system is measured by CHSH inequality.[30]The quantum state violates the CHSH inequality if The CHSH inequality can be written as: The measurement operators MKand M′Kcorrespond to the measurements on the qubit K(K=A,B)with the primed and unprimed terms denoting two different measurement directions.The measurement operators on the second qubit differ by θKfrom that performed on the first qubit: with De fi ning MA≡σyand≡σx,there is a rotation angles θB.The corresponding measurement operators for two-level systems A and B are: Then we calculate the operator expectation value for the quantum state ρ according to the following formula: As to the state ρ0,ρ1,ρ2,we obtain the results after a serious calculation when θB= π/4: We have known that the maximum value of|hB2iρ0|isIt can be seen from Fig.3 that the maximum value of|hB2iρ1|,|hB2iρ2|can be also reached at u=1/2 for a given d.It is different from the measurement of concurrence and QD,the evolution values of|hB2iρ1|and|hB2iρ2|are all proportional to that of the initial state ρ0. Fig.3 The absolute expectation value of Bell inequality|hB2iρ1|and|hB2iρ2|versus the parameter u.The solid and blue line:d=0.2;The dashed and green line:d=0.4;The dotted and red line:d=0.6. Furthermore,Let us discuss the same issues under GADC.A GADC describes the effect of dissipation to an environment at finite temperature.It is defined by and p represents the temperature of the environment.Note that for any p∈[0,1]and any d∈[0,1],the corresponding ε is a quantum channel.When p=0 or 1,the channel is reduced to an ADC.Since p is an indicator of the temperature of the environment,it is likely that one can evaluate the true value of p beforehand,independent of the channel.Without loss of generality,p=1/2 is chosen in the following discussion. Using Eqs.(28)and(29),one can obtain the density matrix in single-sided GADC under initial state ρ0: For convenience,we also assume the strengths of the decohenrence on each qubit are the same when considering that each qubit undergoes the GADC.Then we have the density matrixas: Similarly,the concurrence ofandcan be easily computed: The evolutions of C()and C()with u in a given d are shown in Fig.4.The results show that the residual entanglement reaches its maximum at u=1/2 under not only single-sided but also two-sided GADC.It is different from that of ADC. Quantum discord of ρ′1and ρ′2can also be calculated by Eqs.(15)and(17)with different λ and μ.As for D(ρ′1),the corresponding λ is, For D(),the corresponding μ is Fig.4 The concurrence C(ρ′1)and C(ρ′2)versus the parameter u for a given decoherence strength d.The solid and blue line:d=0.2;The dashed and green line:d=0.4;The dotted and red line:d=0.6. Fig.5 The discord D(ρ′1)and D(ρ′2)versus the parameter u.The solid and blue line:d=0.2;The dashed and green line:d=0.4;The dotted and red line:d=0.6. It can be seen from Fig.5 that the residual QD also reaches its maximum at u=1/2.The evolution of QD is symmetrical to the initial value u.The result is obviously different from that of ADC. By using Eq.(23),we can obtain that, It is interesting that the result of|hB2i|in GADC is the same as that in ADC.That is,|hB2iρ′1|and|hB2iρ′2|are proportional to the initial parameter u. In conclusion,we have investigated the concurrence,QD and CHSH inequality of the bipartite system in ADC and GADC and have obtained some interesting results. We have demonstrated that the evolutions of the concurrence,QD and the CHSH inequality are different from each other in the bipartite system under ADC model.Specifically speaking,in case of one-side noise the concurrence of ρ1is proportional to that of the initial state for a given d.But in two-side noise the concurrence of ρ2is not monotonic to that of the initial state.The result of QD shows that in situation of one-side noise and two-side noise the consequences are both not proportional to that of the initial state.While the absolute Bell-inequality values are all proportional to that of the initial state in single-and two-sided ADC. The reasons of different symmetric and asymmetric consequences are that:the amplitude damping noise makes some information of the system flow away and the different measurements describe different physical substances.Concurrence is a straightforward measurement of entanglement.QD is regarded as a more general measure of nonclassical correlations than entanglement and even survives entanglement.CHSH inequality measures Bell-nonlocality.In essence,these measurements are different but interrelate with each other.The results imply that the evolution of Bell-nonlocality may reveal the characteristics of quantum state better.That is,the initial maximally nonlocal state can maintain its maximally nonlocality characteristic under amplitude damping noise. Furthermore,we can see that both in single-and two-sided GADC model,the evolutions of concurrence,QD and CHSH inequality are all proportional to the initial parameter u.The symmetry between the quantum measurements and the initial parameter u is maintained because that GADC is a non-Markovian physical process which makes the loss information flow back to the system. The results we have obtained may contribute to our understanding of quantum noise and quantum correlations as well as may be of great importance for quantum information processing. References [1]P.J.Dodd and J.J.Halliwell,Phys.Rev.A 69(2004)052105. [2]T.S.Cubitt,F.Verstraete,and J.I.Cirac,Phys.Rev.A 71(2005)052308. [3]Z.Ficek and R.Tanas,Phys.Rev.A 74(2006)024304. [4]W.K.Wootters,Phys.Rev.Lett.80(1998)2245. [5]R.F.Werner,Phys.Rev.A 40(1989)4277. [6]J.Barrett,Phys.Rev.A 65(2002)042302. [7]H.Olivier and W.H.Zurek,Phys.Rev.Lett.88(2001)017901;L.Henderson and V.Vedral,J.Phys.A 34(2001)6899. [8]J.M.Cai,Z.W.Zhou,and G.C.Guo,Phys.Rev.A 72(2005)022312. [9]M.M.Ali,P.W.Chen,and H.S.Goan,Phys.Rev.A 82(2010)022103. [10]J.G.Li,J.Zou,and B.Shao,Phys.Rev.A 82(2010)042318. [11]J.Maziero,L.C.Celeri,R.M.Serra,and V.Vedral,Phys.Rev.A 80(2009)044102. [12]B.You and L.X.Cen,Phys.Rev.A 86(2012)012102. [13]B.Aaronson,R.L.Franco,and G.Adesso,Phys.Rev.A 88(2013)012120. [14]L.Mazzola,J.Piilo,and S.Maniscalco,Int.J.Quantum Inf.9(2011)981. [15]T.Yu and J.H.Eberly,Science 323(2009)598. [16]L.Mazzola,J.Piilo,and S.Maniscalco,Phys.Rev.Lett.104(2010)200401. [17]J.S.Xu,X.Y.Xu,C.F.Li,C.J.Zhang,X.B.Zou,and G.C.Guo,Nature Commun.1(2010)7. [18]T.Konrad,F.de Melo,M.Tiersch,C.Kasztelan,A.Aragao,and A.Buchleitner,Nat.Phys.4(2008)99. [19]O.J.Farias,C.L.Latune,S.P.Walborn,L.Davidovich,and P.H.S.Ribeiro,Science 324(2009)1414. [20]Xin-Wen Wang,Shi-Qing Tang,Ji-Bing Yuan,and Le-Man Kuang,Int.J.Theor.Phys.54(2015)5. [21]T.Yu and J.H.Eberly,Phys.Rev.B 68(2003)165322.[22]K.Kruas,States,effect,and Operations:Fundamental Notions in Quantum Theory,Springer-Verlag,Berlin(1993). [23]B.Schumacher and M.D.Westmoreland,Phys.Rev.A 74(2006)042305. [24]T.Yu and J.H.Eberly,Quantum Inf.Comput.7(2007)459. [25]A.R.P.Rau,J.Phys.A 42(2009)412002. [26]S.Luo,Phys.Rev.A 77(2008)042303. [27]G.Jaeger and K.Ann,Phys.Lett.A 372(2008)2212. [28]Q.Yang,M.Yang,and Z.L.Cao,Phys.Lett.A 372(2008)6843. [29]X.L.Zhen,Q.Yang,M.Yang,and Z.L.Cao,Commun.Theor.Phys.62(2014)795. [30]J.F.Clauser,M.A.Horne,A.Shimony,and R.A.Holt,Phys.Rev.Lett.23(1969)880.2.2 Quantum Discord

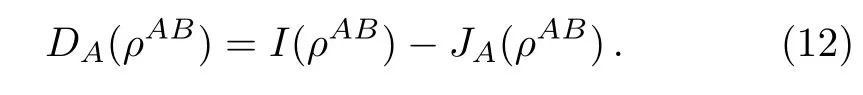
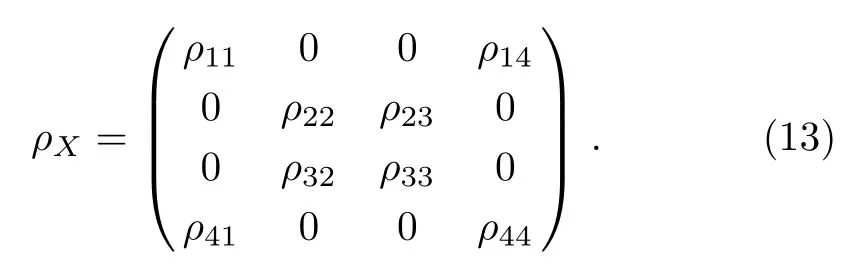
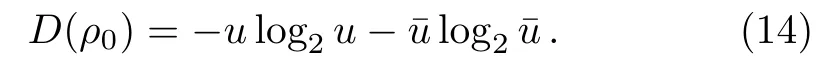


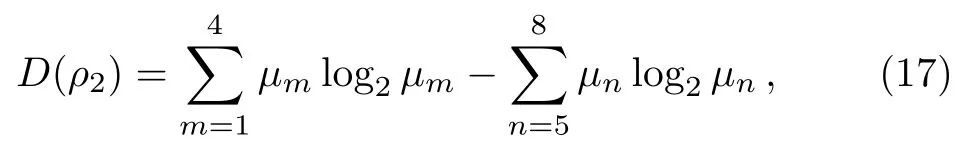
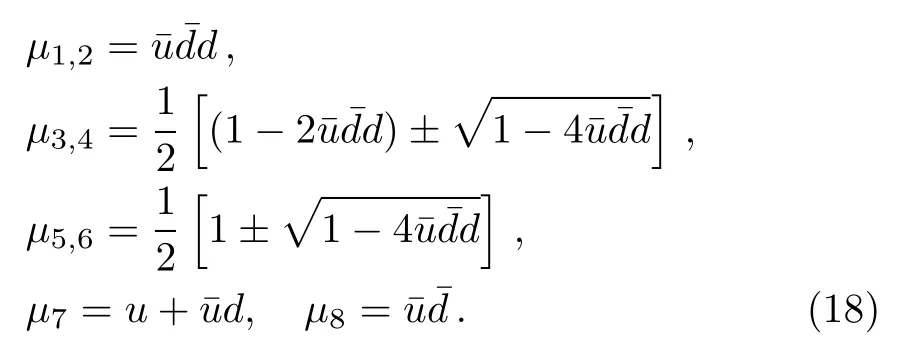
2.3 Bell Nonlocality


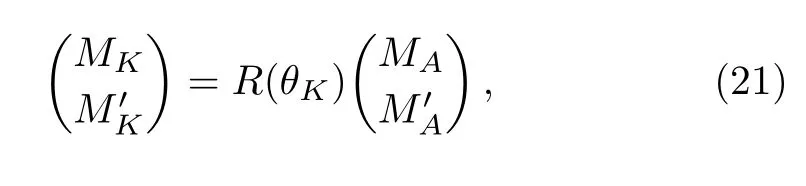
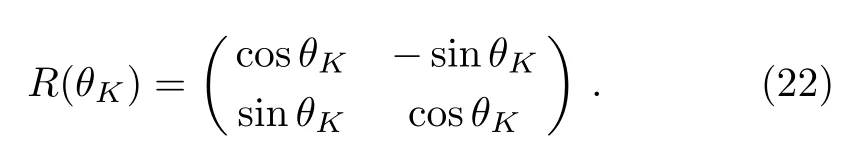
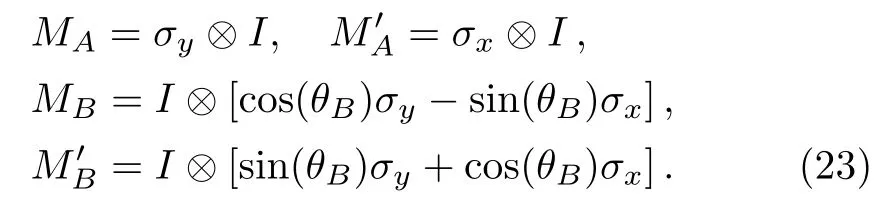

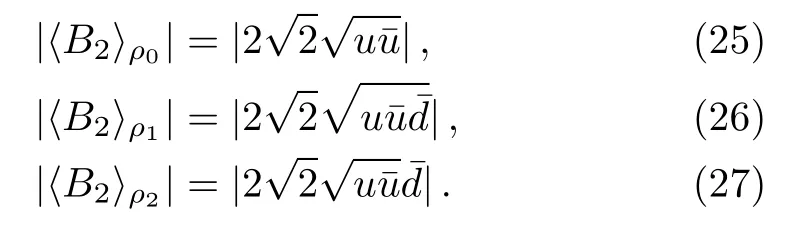
3 GADC Model
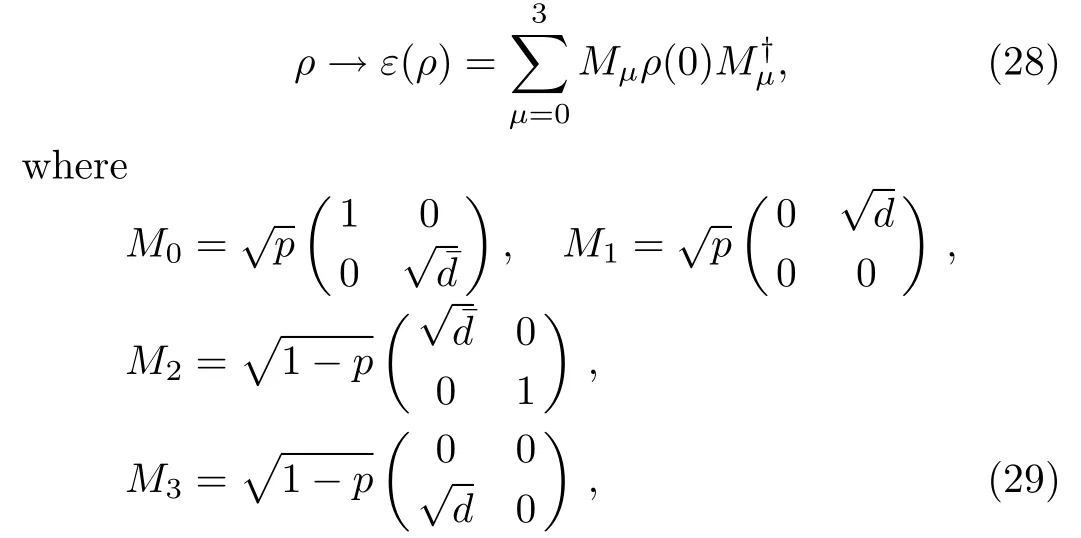

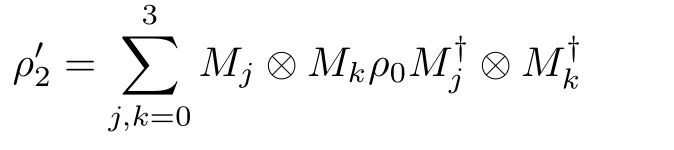

3.1 Concurrence
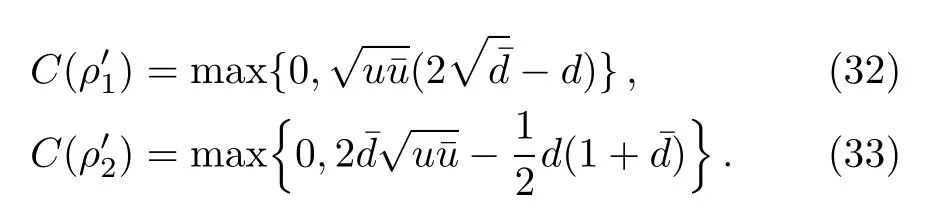
3.2 Quantum Discord



3.3 Bell Nonlocality
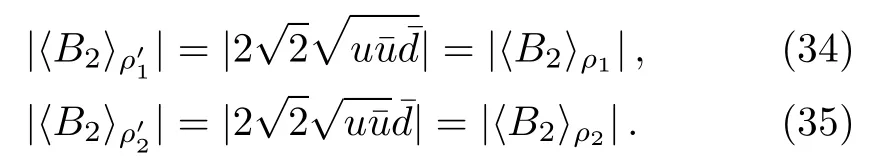
4 Conclusion
 Communications in Theoretical Physics2016年3期
Communications in Theoretical Physics2016年3期
- Communications in Theoretical Physics的其它文章
- An Improved Discrete-Time Model for Heterogeneous High-Speed Train Traffic Flow?
- Thermal Magni fi er and Mini fier?
- Extracting Structure Parameters of Dimers for Molecular Tunneling Ionization Model?
- Statistical Law of High-Energy Fullerene and Its Derivatives Passing Through Graphene?
- Re-examining Photodetachment of H?near a Spherical Surface using Closed-Orbit Theory?
- Electronic Structure of Helium Atom in a Quantum Dot?
