Deng-Shan Wang(王燈山), Xiang-Gui Li(李祥貴), C.K.Chan(陳昌麒), and Jian Zhou(周健)

1School of Applied Science,Beijing Information Science&Technology University,Beijing 100192,China

2Department of Applied Mathematics,The Hong Kong Polytechnic University Kowloon,Hong Kong,China

1 Introduction

Analytic and explicit solutions of nonisoscpectral equations are important in modern physics,as they are related to time-dependent spectral parameter and helpful in the understanding of the physical meanings of the nonisoscpectral systems,which provide many realistic models in physical situations.Inverse scattering transform,[1]Hirota method,[2]and Wronskian technique,[3?4]Darboux transformation,[5]B¨acklund transformations,[6?7]variable separation method,[8]Lie symmetry method,[9]similarity transformation method[10?14]and direct ansatz method[15?16]are efficient approaches for finding exact solutions of such nonisospectral equations.Among these approaches,the Wronskian technique,[4]which was first proposed by Satsuma[3]and then developed by Nimmo and Freeman,[4]is a powerful tool for constructing Wronskian solutions of integrable equations.Compared with the inverse scattering transform,Darboux transformation and Hirota method,the Wronskian technique is more directly to find the soliton solutions,rational solutions,negaton and positon solutions and complexiton solutions in term of Wronskian determinants.Darboux transformation and Hirota method can give N-soliton solutions as an N-th order polynomial in exponential form,but it is very hard to verify such N-soliton solutions.On the contrary,the N-soliton solutions expressed by Wronskian determinant are relatively easier to be verified.Moreover,the double Wronskian solutions are general exact solutions of integrable equations,which can reveal abundant nonlinear structures of integrable systems.

Recently,much attention has been paid on the exact solutions of nonisospectral soliton equations.Deng et al.,[17]Bi et al.,[18]Sun et al.,[19]Sun,[20]You et al.,[21]and Ji[22]have obtained some exact solutions for different kind of nonisospectral equations.Numerical method is a supplement of the nonisospectral problem.[23?25]

For the nonisospectral GSK equation,N-soliton solutions were obtained by Zhou et al.,[26]and the Wronskian solution and soliton resonance were also discussed by Zhou et al.[27]

The nonisospectral BKP equation and other soliton equations were derived by Chen et al.[28]and Deng[29]provided the bilinear form of the nonisospectral BKP equation by using the Hirota method.[30]The nonisospectral BKP equation is given by

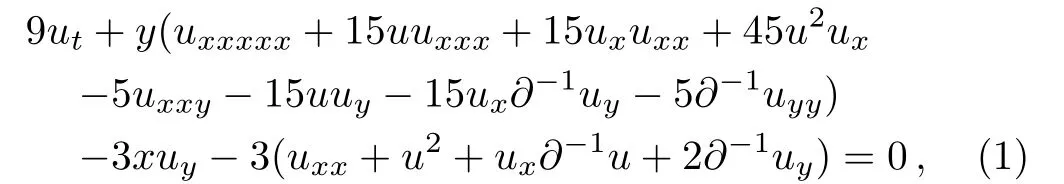
which has Lax pair in form of[28]

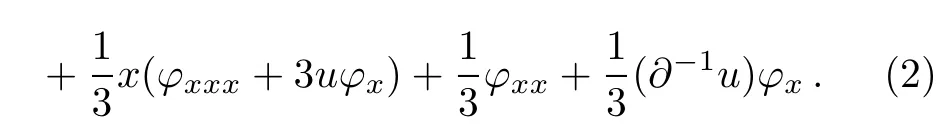
In this work,double Wronskian conditions of the nonisospectral BKP equation are presented.We take the onesoliton and two-soliton solutions as examples to investigate the dynamical influence and soliton resonance.In Sec.2,double Wronskian conditions of the nonisospectral BKP equation are derived by the Wronskian technique.In Sec.3,examples and figures are given to show soliton properties and the proof of double Wronskian solution is provided in the Appendix.

2 The Double Wronskian Conditions

By means of the dependent variable transformation

Eq.(1)can be written in the bilinear form[29]

where the D-operator[30]is defined by

The solution of Eq.(4)can be written in double Wronskian form as

where ? and ψ satisfy

Using D-operator in Eq.(5),the bilinear equation in Eq.(4)can be rewritten as

Substituting the function f as defined in Eq.(6)into Eq.(8),it can be shown that this function is the solution of Eq.(8).Details are shown in the Appendix.

3 Dynamical Properties of Solitons

From the Wronskian conditions in Eq.(7),the double Wronskian solution of Eq.(1)is obtained in Eq.(3)with Eq.(6)and

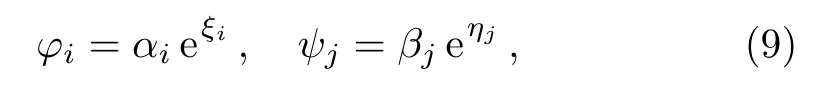
where

and αi,βjare constants.

3.1 One-Soliton Properties

Taking M=N=0,α1= α2= β2=1,β1= ?1,we obtain

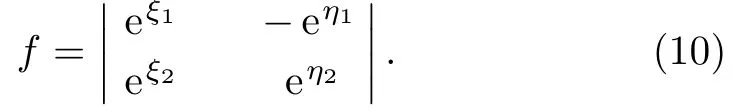
Substituting Eq.(10)into the transformation(3)and Eqs.(6)and(9),we have

which is a one-soliton solution,and it can be seen that this one-soliton travels with a time-dependent top trace

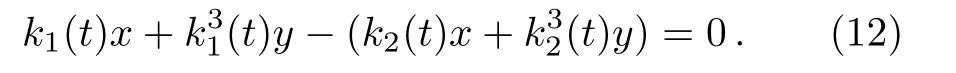
In fact,the top trace given by Eq.(12)is a line with time-dependent slope. Equation(11)provides a linesoliton with the time-dependent amplitude

When t= ?3c1or t= ?3c2,there is a blow-up in this solution.Figures 1 and 2 show the shape and motion of the one soliton in Eq.(11)with time-dependent amplitude and slope.

The different shape and amplitude of the soliton(10)at t=1 and t=2 are illustrated by Figs.1 and 2.Moreover,the dynamical influences of one soliton with the speed and the shape of the one soliton at different time are shown in Figs.3 and 4.

Solving x from Eq.(12),we have

The speed is obtained by Eq.(14)such that

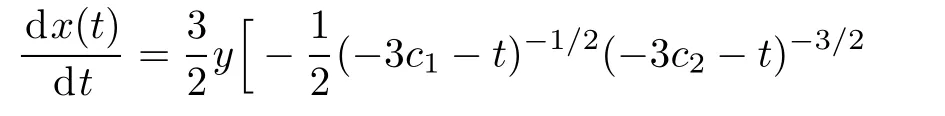
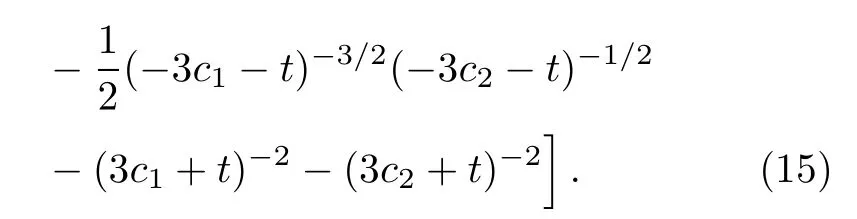
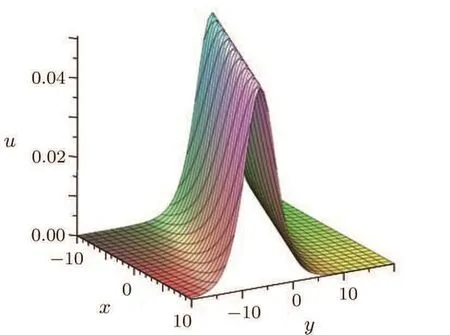
Fig.1 The shape and motion of the one-soliton solution in double Wronskian form given by Eq.(11)at t=1 with parameters c1=?1 and c2=?2.

Fig.2 The shape and motion of the one-soliton solution in double Wronskian form given by Eq.(11)at t=2 with parameters c1=?1 and c2=?2.

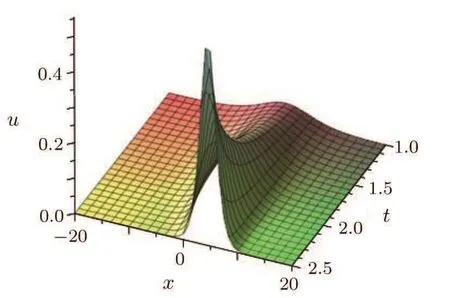
Fig.3 3D plot of the one-soliton solution in Eq.(11)at y=1 with parameters c1=?1 and c2=?2.

In this case,the speed of the soliton varies with time and this time-dependent property comes from the effects of inhomogeneous media.The shapes of the soliton are illustrated in Fig.4,which shows that the one soliton in Eq.(11)is not symmetric,and for fixed y=1 the amplitudes of the soliton increase in time.

Fig.4 2D plots of the one-soliton solution in Eq.(11)at y=1 and time t=0,1,2 with parameters c1=?1 and c2=?2.

3.2 Two-Soliton Interaction Properties

In this section,the two-soliton interaction properties of the nonisospectral BKP equation(1)are investigated by considering three cases of Eq.(6).

(i)M=0,N=1.

Taking M=0,N=1,αi=1(i=1,2,3),β1= β3=1,β2= ?1,we obtain

Substituting the Wronskian determinant(16)into the bilinear transformation(3),we obtain the two-soliton solution to the nonisospectral BKP equation(1)as

where ξ1,ξ2,ξ3,η1,η2,η3are determined by Eq.(9).

(ii)M=1,N=0.

Taking M=1,N=0,βi=1(i=1,2,3),α1= α3=1,α2= ?1,we obtain

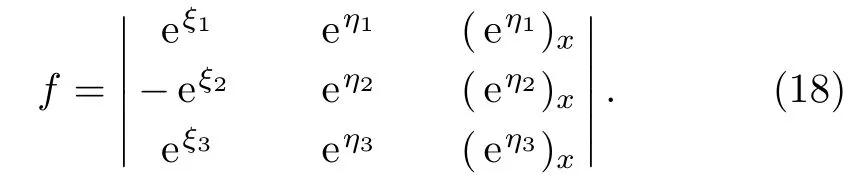
Substituting the Wronskian determinant(18)into the bilinear transformation(3),we obtain the two-soliton solution to the nonisospectral BKP equation(1)as

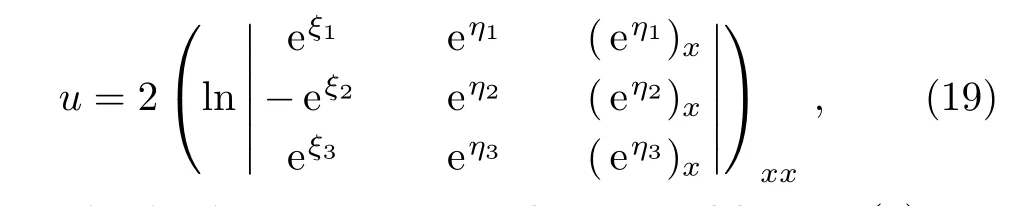
where ξ1,ξ2,ξ3,η1,η2,η3are determined by Eq.(9).

Interesting nonlinear structures of the two-soliton solutions in Eqs.(17)and(19)are presented by means of some density distributions.We hope this type of figures can also describe the properties of soliton resonance.In Figs.5 and 6,it can be seen that the two-soliton solutions expressed by double Wronskian forms have three arms with each of them being line-soliton.Such asymptotic behavior results in the so-called resonance of the line solitons.The difference between Figs.5 and 6 is the bifurcation position,which results from the choice of integers M and N in Eq.(9).In this case,the amplitudes and slopes of the three arms vary with time and this time-dependent property comes from the effects of inhomogeneous media.

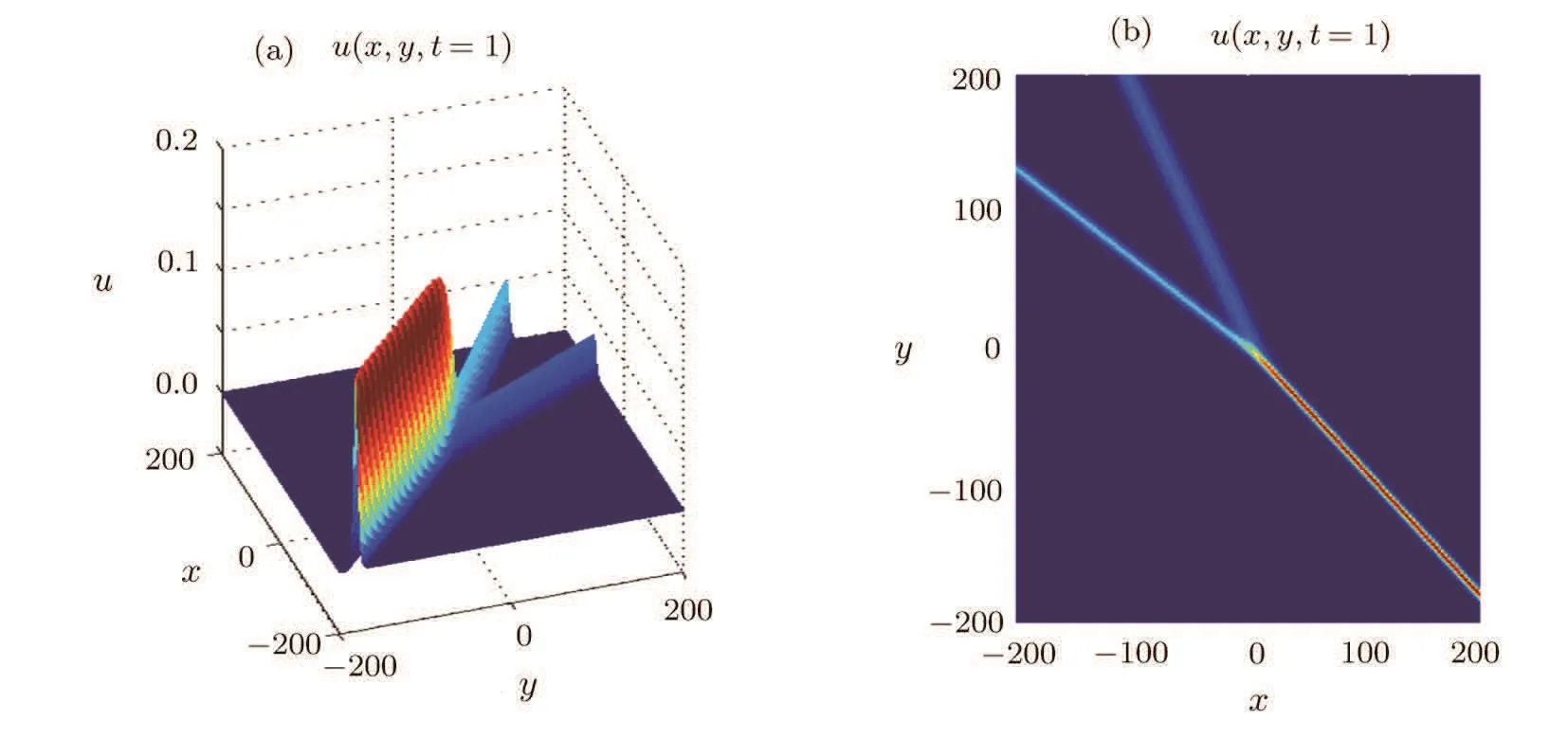
Fig.5 The shape and contour of the two-soliton solution(17)at t=1 for parameters c1=?1,c2=?2,c3=?6.

Fig.6 The shape and contour of the two-soliton solution(19)at t=1 for parameters c1=?1,c2=?2,c3=?6.

(iii)M=1,N=1.

Taking M=1,N=1,αi= βi=1(i=1,2,3,4),we obtain from Eq.(9)that

Substituting the Wronskian determinant(20)into the bilinear transformation(3),we obtain the third two-soliton solution to the nonisospectral BKP equation(1)as

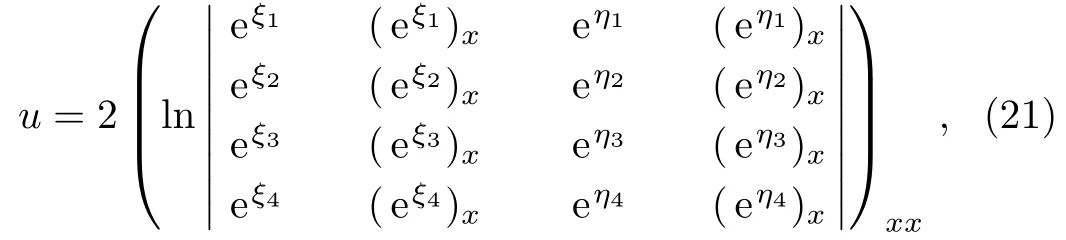
where ξ1, ξ2, ξ3, ξ4, η1, η2, η3, η4are determined by Eq.(9).Figure 7 shows the shape and contour of this two-soliton solution.It is observed that the two-soliton solution in Eq.(21)displays a classical two-soliton interaction,which is usual in isospectral KP-type equation.

Fig.7 The shape and contour of the two-soliton solution(21)at t=1 for parameters c1=?1,c2=?2,c3=?3,and c4=?4.

4 Conclusion

In this paper,the double Wronskian solution for the nonisospectral BKP equation is obtained by Wronskian technique.Some figures are presented to show that certain solitons are not symmetric in shape.Soliton resonances are discussed by density distributions.Moreover,dynamical influences of the solitons are also investigated in the inhomogeneous media.

Appendix

In this appendix,we demonstrate that the function f defined in Eq.(6)is the solution of Eq.(8).It is known that[30]

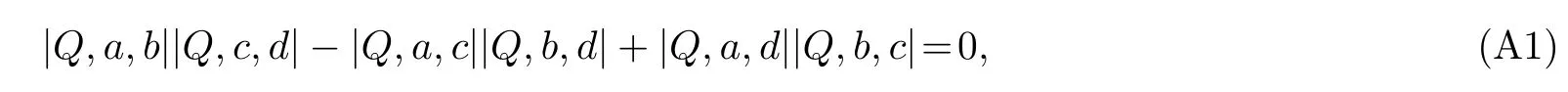
where Q is an N×(N?2)matrix,and a,b,c,d are N-dimensional column vectors.

Then

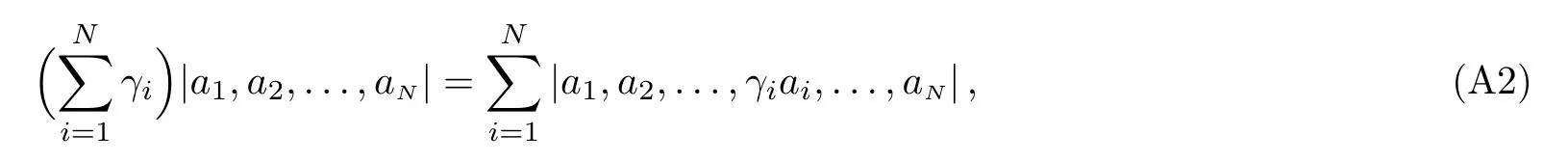
where γajis a column vector,i.e.γaj=(γ1a1j,γ2a2j,...,γnanj)T.From Eq.(7),the l-th order derivatives of ?i,tand ψj,twith respect to x are

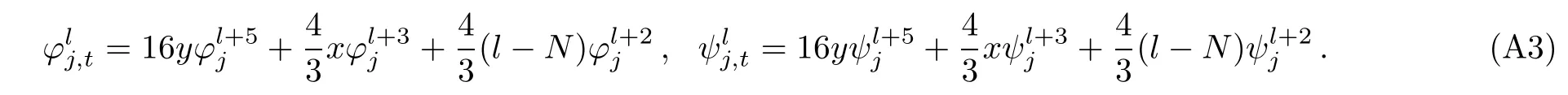
Using Eqs.(7)and(A3),we calculate partial derivatives of the function defined in Eq.(6)with respect to x,y,t as

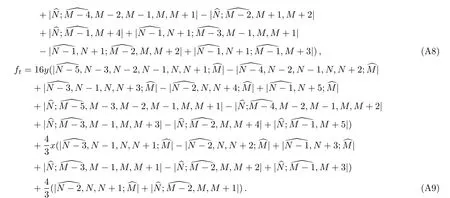
Substituting Eqs.(A4)–(A9)into left-hand side of Eq.(8),we have

where

and using Plcker condition(A1),we have

Further substituting Eqs.(A13)–(A16)into Eq.(A12),we have

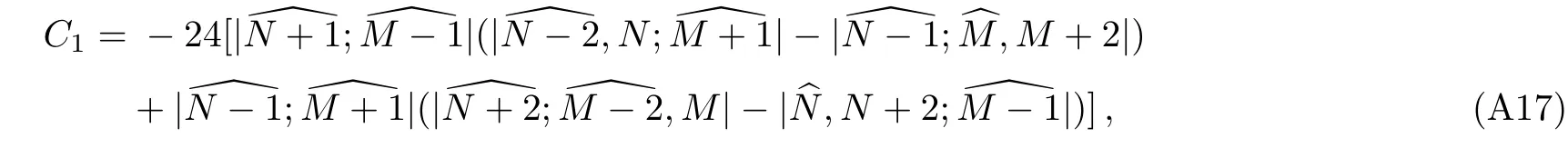
and substituting

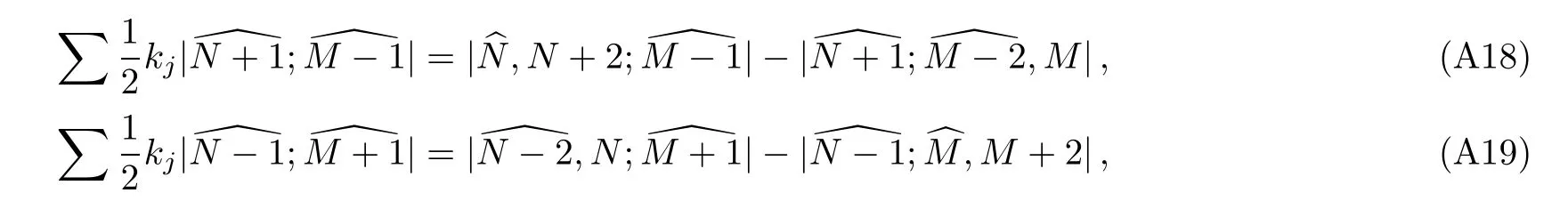
into Eq.(A17),we have

In the same way,it is easy to see

Therefore,the function f determined by Eq.(6)is the solution of Eq.(8).This ends the proof.

References

[1]M.J.Ablowitz and H.Segur,Solitons and the Inverse Scattering Transform,SIAM,Philadelphia(1981).

[2]R.Hirota,Phys.Rev.Lett.27(1971)1192.

[3]J.Satsuma,J.Phys.Soc.Jpn.46(1979)359.

[4]J.J.C.Nimmo and N.C.Freeman,Phys.Lett.A 95(1983)4.

[5]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer,Berlin(1991).

[6]W.Strampp,W.Oevel,and H.Steeb,Lett.Math.Phys.7(1983)445.

[7]X.Lu,F.Lin,and F.Qi,Appl.Math.Model.39(2015)3221.

[8]X.Y.Tang and S.Y.Lou,J.Math.Phys.44(2003)4000.

[9]S.Y.Lou,X.R.Hu,and Y.Chen,J.Phys.A:Math.Gen.45(2012)155209.

[10]H.P.Zhu,Nonlinear Dyn.76(2014)1651.

[11]C.Q.Dai,Y.Y.Wang,and X.F.Zhang,Opt.Express 22(2014)29862.

[12]D.S.Wang,X.H.Hu,J.P.Hu,and W.M.Liu,Phys.Rev.A 81(2010)025604.

[13]D.S.Wang,X.H.Hu,and W.M.Liu,Phys.Rev.A 82(2010)023612.

[14]D.S.Wang,S.W.Song,B.Xiong,and W.M.Liu,Phys.Rev.A 84(2011)053607.

[15]C.Q.Dai,X.G.Wang,and G.Q.Zhou,Phys.Rev.A 89(2014)013834.

[16]Y.X.Chen,Nonlinear Dyn.79(2015)427.

[17]S.F.Deng,D.J.Zhang,and D.Y.Chen,J.Phys.Soc.Jpn.74(2005)2383.

[18]J.B.Bi,Y.P.Sun,and D.Y.Chen,Physica A 364(2006)157.

[19]Y.P.Sun,J.B.Bi,and D.Y.Chen,Chaos,Solitons and Fractals 26(2005)905.

[20]Y.P.Sun,Appl.Math.Comput.217(2010)1639.

[21]F.C.You and J.Zhang,Commun.Theor.Phys.56(2011)11.

[22]J.Ji,Phys.Lett.A 372(2008)6074.

[23]X.G.Li,W.Yan,and C.K.Chan,Numer.Math.94(2003)315.

[24]D.Y.Hua and X.G.Li,App.Math.Comput.234(2014)214.

[25]X.G.Li,J.Zhu,R.P.Zhang,and S.Cao,J.Comput.Phys.275(2014)363.

[26]J.Zhou,X.G.Li,and D.S.Wang,Adv.Math.Phys.2014(2014)Article ID 547692.

[27]J.Zhou,X.G.Li,and D.S.Wang,Z.Naturforsch.A 70(2015)213.

[28]D.Y.Chen,H.W.Xin,and D.J.Zhang,Chaos,Solitons and Fractals 15(2003)761.

[29]S.F.Deng,Commun.Theor.Phys.49(2008)535.

[30]R.Hirota,The Direct Methods in Soliton Theory,Cambridge University Press,Cambridge(2004).