Yujian Jiao,Sheng Chen and Benyu Guo

1Department of Mathematics,Shanghai Normal University,Shanghai,200234,P.R.China.Scientific Computing Key Laboratory of Shanghai Universities.E-institute for Computational Science of Shanghai Universities.

2School of Mathematical Sciences,Xiamen University,Xiamen 361005,Fujian Province,P.R.China.

Non-Isotropic Jacobi Spectral and Pseudospectral Methods in Three Dimensions

Yujian Jiao1,?,Sheng Chen2and Benyu Guo1

1Department of Mathematics,Shanghai Normal University,Shanghai,200234,P.R.China.Scientific Computing Key Laboratory of Shanghai Universities.E-institute for Computational Science of Shanghai Universities.

2School of Mathematical Sciences,Xiamen University,Xiamen 361005,Fujian Province,P.R.China.

.Non-isotropic Jacobi orthogonal approximation and Jacobi-Gauss type interpolation in three dimensions are investigated.The basic approximation results are established,which serve as the mathematical foundation of spectral and pseudospectral methods for singular problems,as well as problems defined on axisymmetric domains and some unbounded domains.The spectral and pseudospectral schemes are provided for two model problems.Their spectral accuracy is proved.Numerical results demonstrate the high efficiency of suggested algorithms.

AMS subject classifications:65N35,41A10,41A63

Jacobi spectral and pseudospectral methods in three dimensions,singular problems.

1 Introduction

The main advantage of spectral and pseudospectral methods is their high accuracy,see[3,6–13].In actual computations,the pseudospectral method is more preferable,since it only needs to evaluate unknown functions at interpolation nodes and so simplifies calculations.Moreover,it is much easier to deal with nonlinear terms.However,these merits may be destroyed by singularities of genuine solutions of considered problems,which could be caused by several factors,such as degenerating coefficients of derivatives of different orders involved in underlying problems.For solving such problems,Guo[16,17],and Guo and Wang[24]developed the Jacobi orthogonal approximation and the Jacobi-Gauss type interpolation in non-uniformly weighted Sobolev space,andproposed the corresponding Jacobi spectral and pseudospectral methods with their applications to one-dimensional singular differential equations.We also refer to the work of[1,11,26].The Jacobi spectral method is also useful for numerical solutions of differential equations defined on axisymmetric domains and some unbounded domains,see,e.g.,[2,14,15,18,19,31].Besides,the Jacobi orthogonal approximation and Jacobi-Gauss type interpolation are related to various rational spectral and pseudospectral methods,see[4,5,10,21,22,27,28,32].Recently,Guoet al.[20],and Guo,et al.[23]studied the generalized Jacobi orthogonal and quasi-orthogonal approximations respectively,and so enlarge their applications.In practice,it is more important and interesting to solve the multi-dimensional singular problems and the related problems numerically.Guo and Wang[25]provided the Jacobi spectral method in two-dimensions,while Guo and Zhang[29]investigated the Jacobi pseudospectral method for two-dimensional problems.But there is few existing work dealing with three-dimensional problems by using the Jacobi spectral and pseudospectral methods.

This work is devoted to the Jacobi spectral and pseudospectral methods in threedimensions.We first establish some results on the Jacobi orthogonal approximation,which play important role in designing and analyzing the Jacobi spectral method.Then,we consider the Jacobi-Gauss type interpolation,serving as the basic tool of the Jacobi pseudospectral method.We also derive a series of sharp results on the Legendre-Gauss type interpolation and the related Bernstein-Jackson type inequalities in three-dimensional space,which are very useful for pseudospectral method of partial differential equations with non-constant coefficients.As some applications of the above results,we provide the spectral and pseudospectral methods for a model problem.The numerical results demonstrate the high efficiency of the suggested algorithms and confirm the analysis well.

The paperis organized as follows.In the nextsection,we recall the basic results on the one-dimensional Jacobi orthogonal approximation and Jacobi-Gauss type interpolation.In Sections 3 and 4,we study the three-dimensionalJacobi orthogonalapproximation and Jacobi-Gauss type interpolation,respectively.In Section 5,we propose the Jacobi spectral and pseudospectral methods for three-dimensional problems.In Section 6,we present some numerical results to demonstrate the efficiency of the proposed methods.The final Section is for some concluding remarks.

2 Preliminaries

2.1 Jacobi orthogonal approximation in one dimension

We now recall some results on the Jacobi orthogonal approximation in one dimension.Let Λ=(?1,1)andα,β＞?1.The Jacobi polynomials of degreelare given by

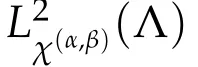
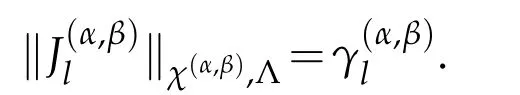
Let N be the set of all nonnegative integers.For anyN∈N.PN(Λ)stands for the set of all algebraic polynomials of degree at mostN.Further,

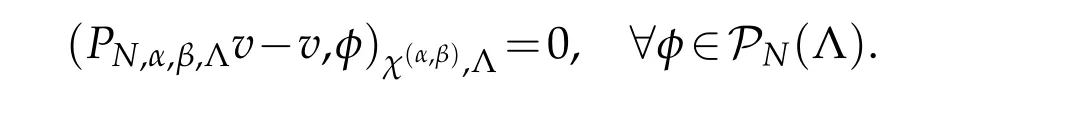
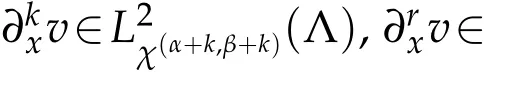
Next,we letα,β,γ,δ＞?1,and define the spaceH1α,β,γ,δ(Λ)with the norm

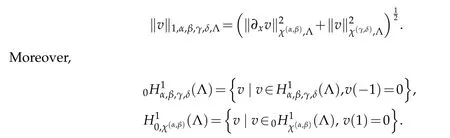
We introduce the bilinear form

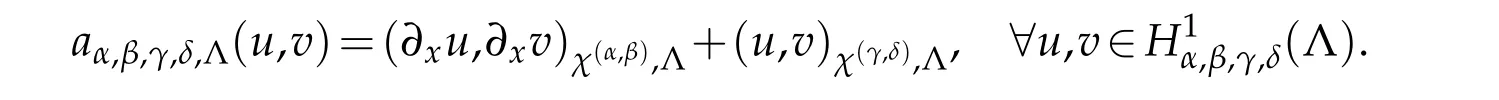
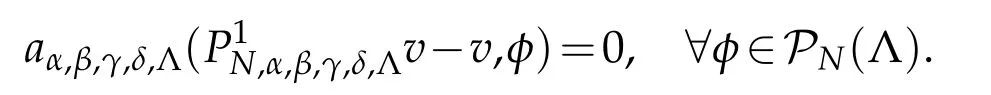
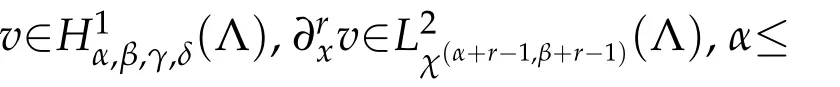
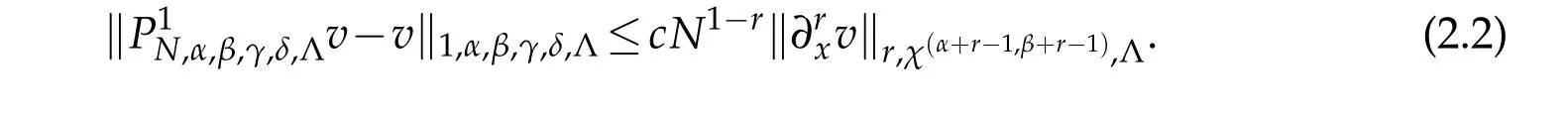
If,in addition,α≤γ+1,β≤δ+1,then

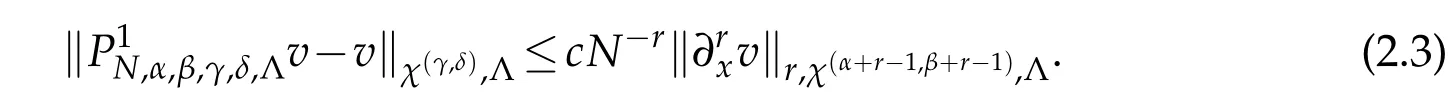
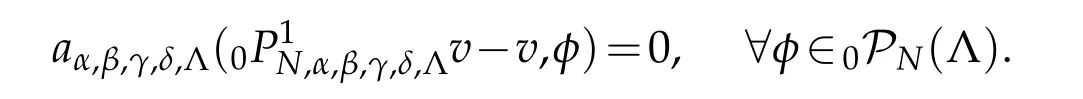
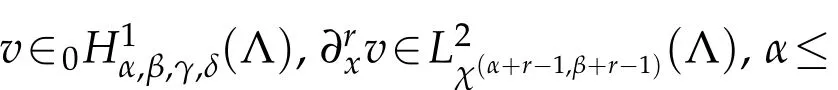
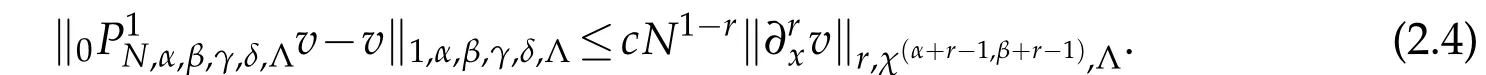
If,in addition,α≤γ+1,β≤δ+1,then

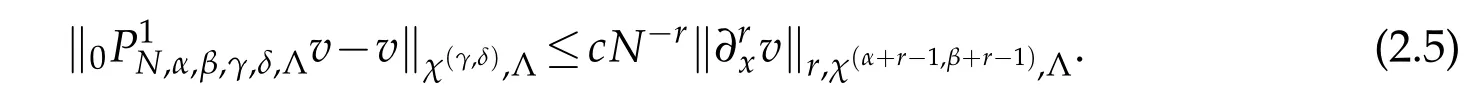
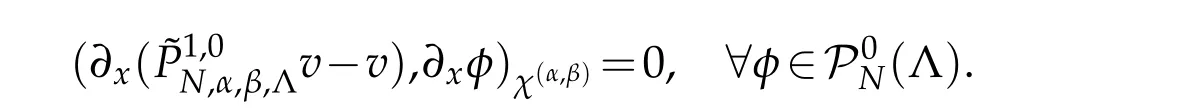
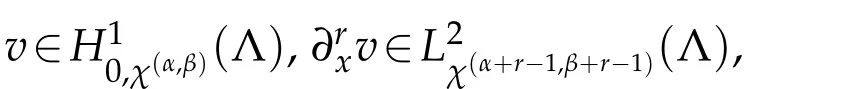
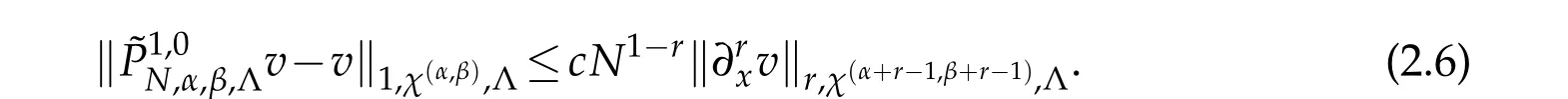
If,in addition,?1＜α,β＜0(or 0＜α,β＜1),then

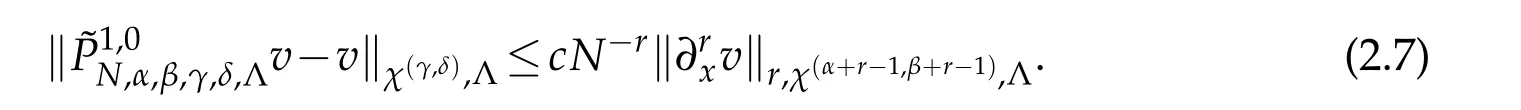
2.2 Jacobi-Gauss type interpolation in one dimension

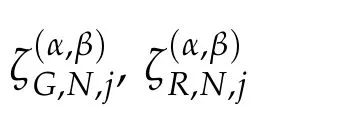
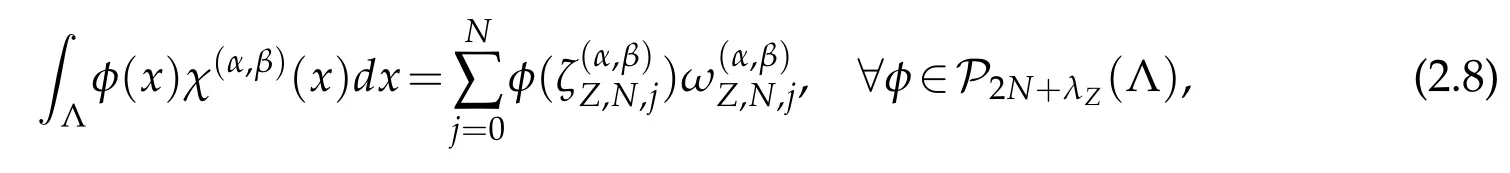
whereλZ=1 forZ=G,λZ=0 forZ=R,andλZ= ?1 forZ=L,respectively.The corresponding discrete inner product and norm are as follows,

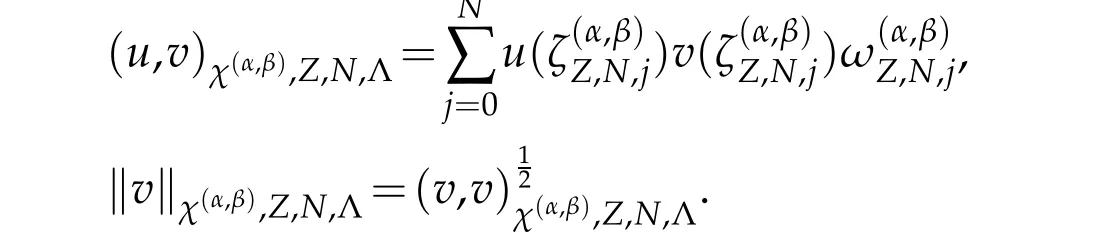
By the exactness of(2.8),we have

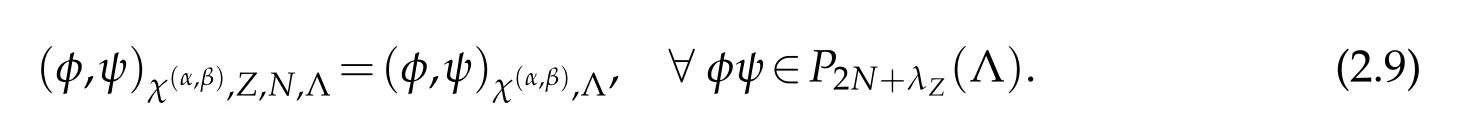
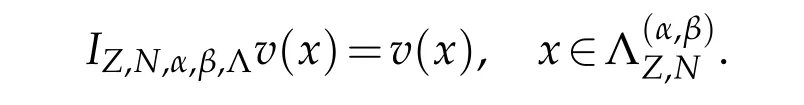
They are named as the Jacobi-Gauss interpolation for Z=G,the Jacobi-Gauss-Radau interpolation for Z=R,and the Jacobi-Gauss-Lobatto interpolation for Z=L,respectively.

According to Theorems 4.1,4.5 and 4.9 of[26],we have the following results.

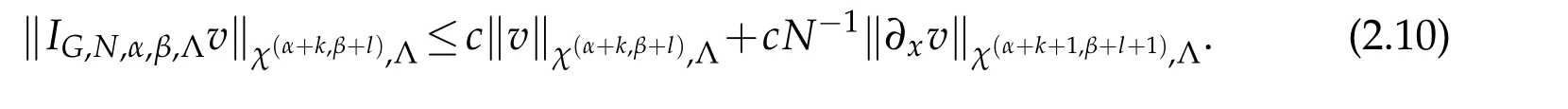
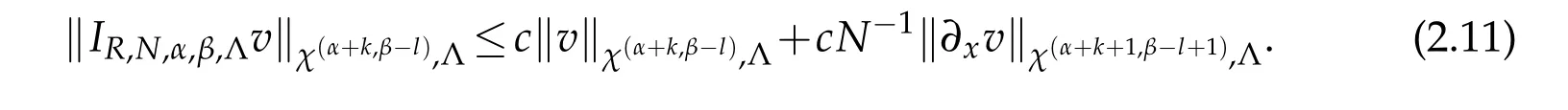
then

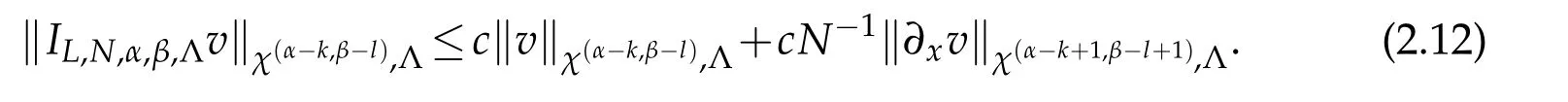
Furthermore,as the special cases of Theorems 4.2,4.6 and 4.10 of[26],we have the following approximation results.

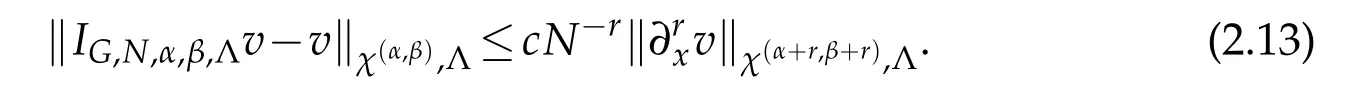
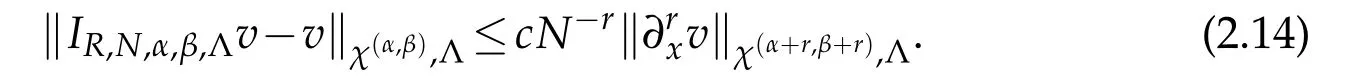
then

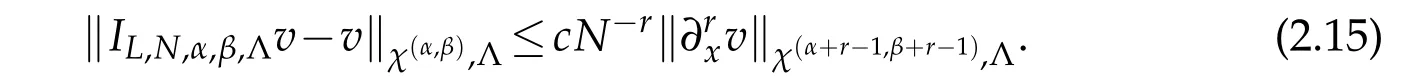
We now focus on the Legendre-Gauss interpolation.The result(2.15)withα=β=0 andr=1 implies

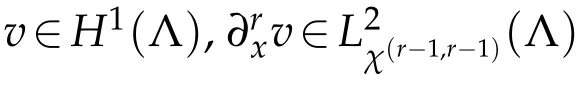
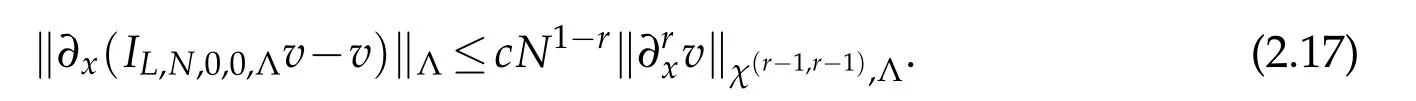
The above inequality withr=1 implies

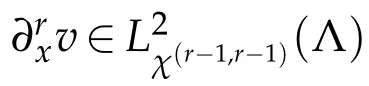
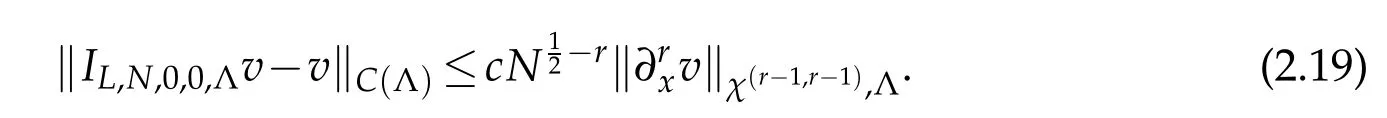
This is a Bernstein-Jackson type inequality.

3 Jacobi orthogonal approximation in three dimensions

In this section,we study the non-isotropic Jacobi orthogonal approximation in three dimensions.We set Λi={xi|?1＜xi＜1},i=1,2,3, ?=Λ1×Λ2×Λ3andx=(x1,x2,x3).The inner product and norm of the weighted spaceL2χ(?)are denoted by(u,v)χ,?and‖u‖χ,?,respectively.

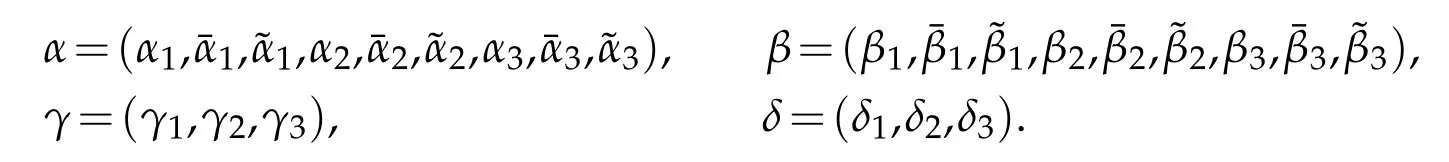
The three-dimensional Jacobi weight functions are as follows,

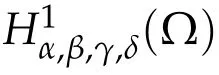
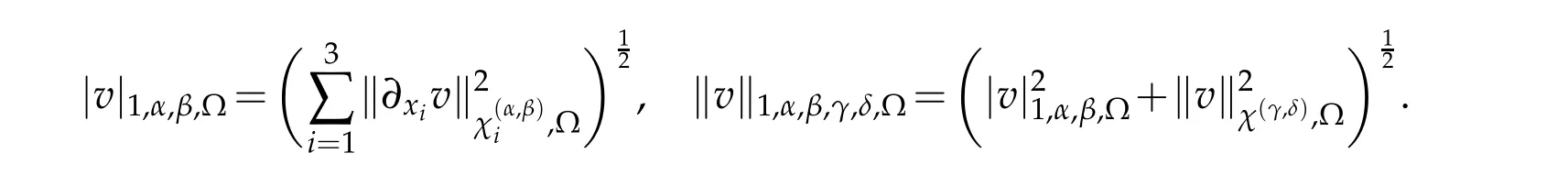
ForN=(N1,N2,N3)∈N3,PN(?)stands for the set of all algebraic polynomials of degree at mostNiwith respect toxi,i=1,2,3.

In order to describe the approximation error,we letr=(r1,r2,r3),ri∈N,and

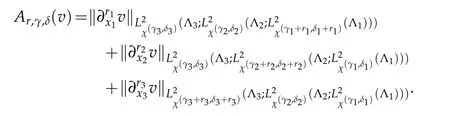
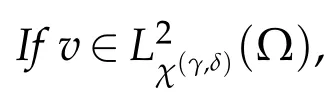
then

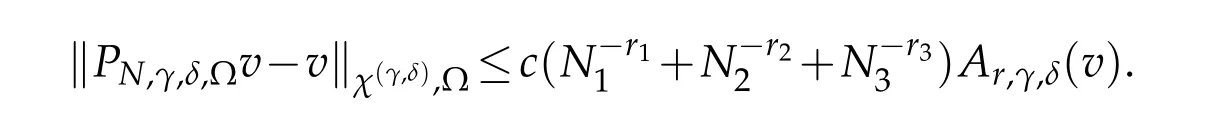
Proof.LetPNi,γi,δi,Λi,i=1,2,3,be the one-dimensional projections as in the last section.We use projection theorem and(2.1)withk=0 andr=rior 0 to derive that

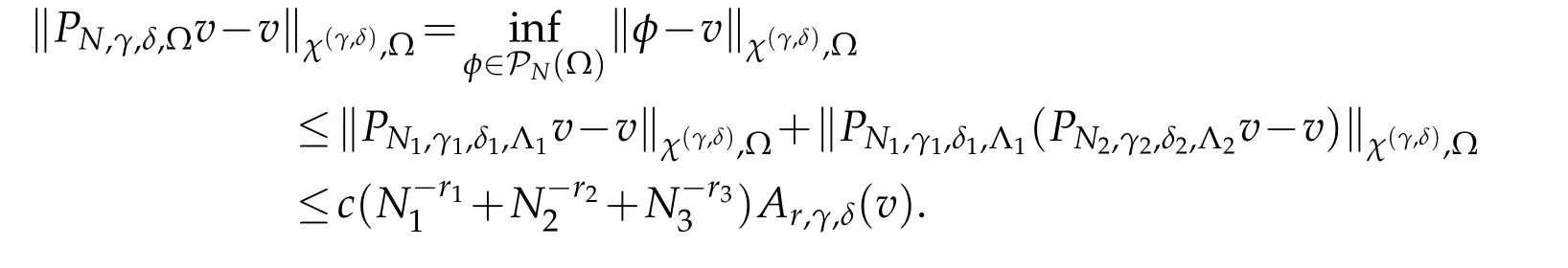
This completes the proof of the theorem.

Next,let

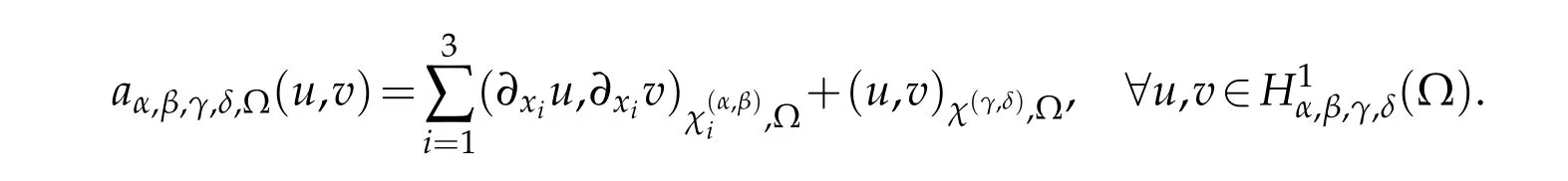
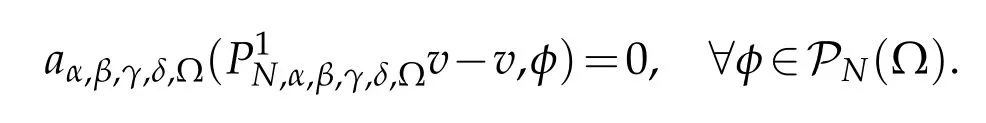
We introduce the following quantity

Theorem 3.2.Let

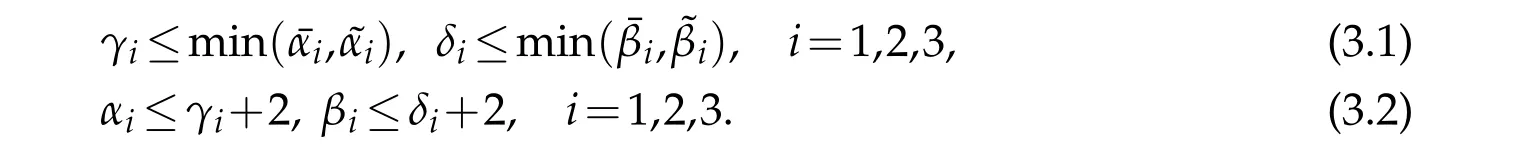
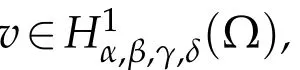
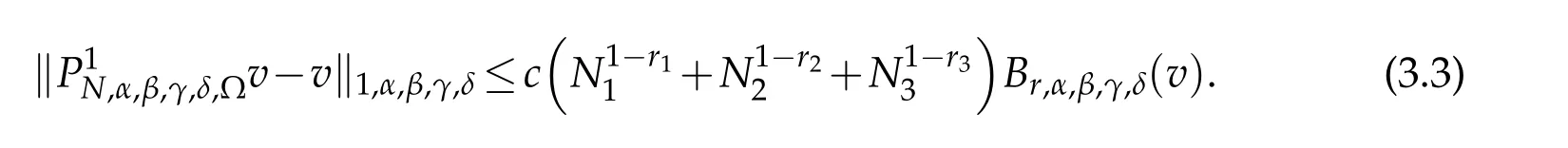
If in addition,if

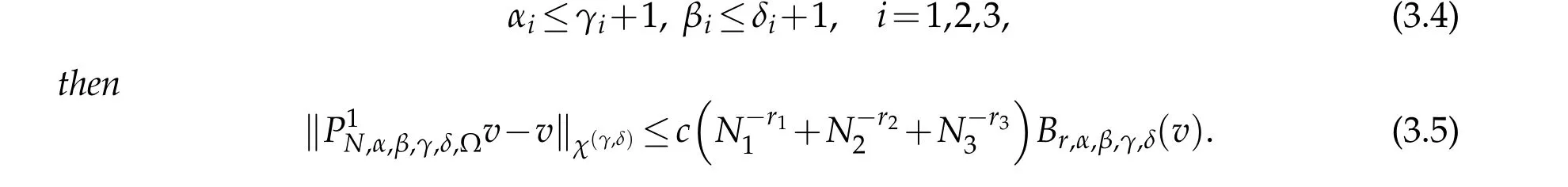
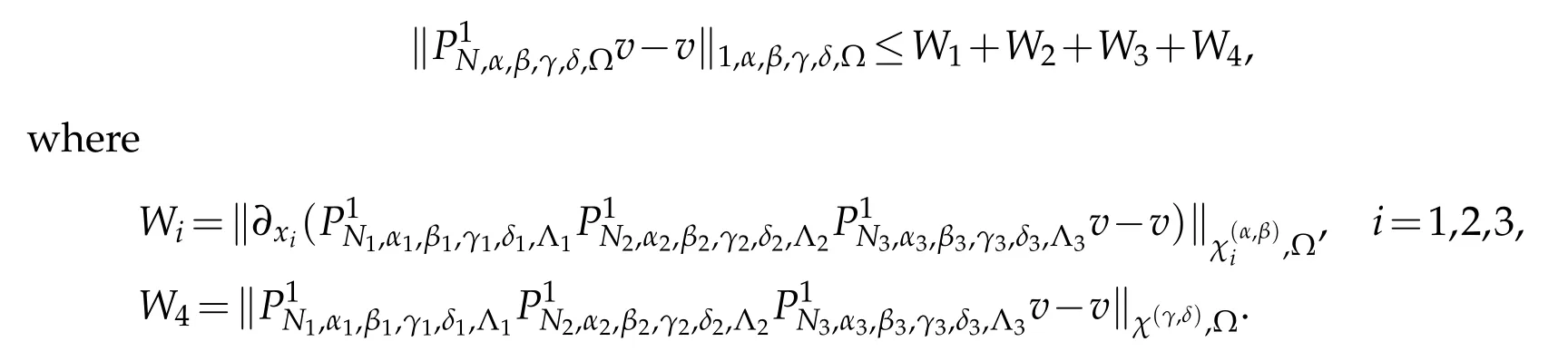
We have(cf.[26])

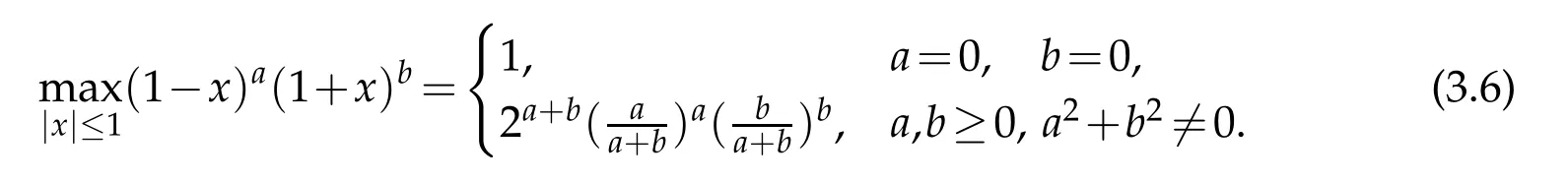
Thus,we use(3.1)to obtain

Using(3.7)and(2.2)withr=1,we have that

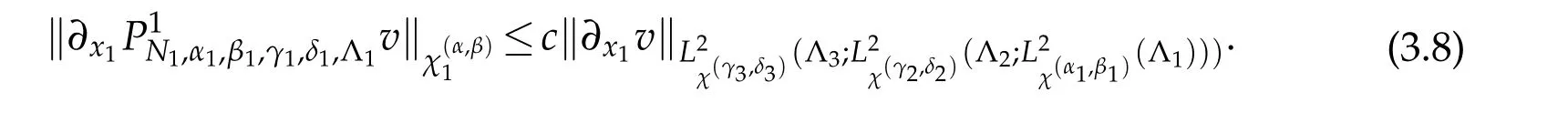
We now estimateW1.

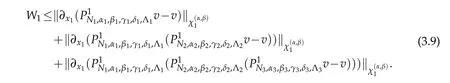
By using(3.7)and(2.2),we derive that

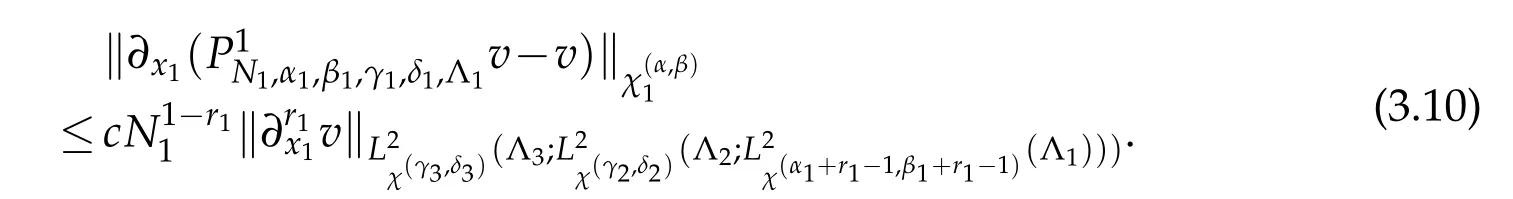
According to(3.8)and(2.2),we deduce that

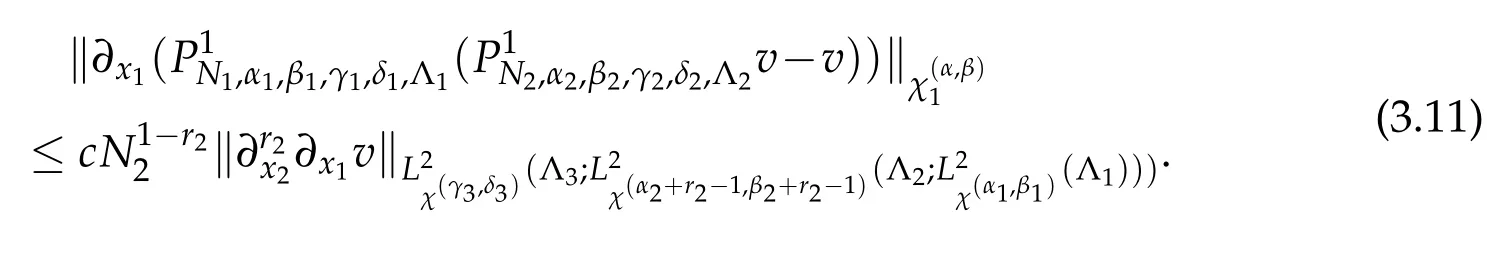
Using(3.8),(2.2)withr=1 and(2.2)withr=r3,we derive that

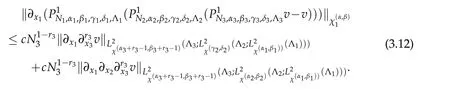
Substituting(3.10)-(3.12)into(3.9),we get that

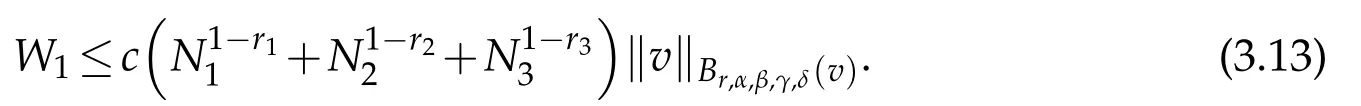
Similarly,we can check that

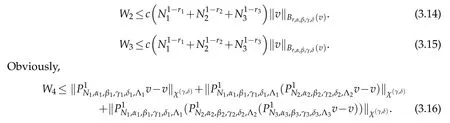
Thanks to(2.2),we have that

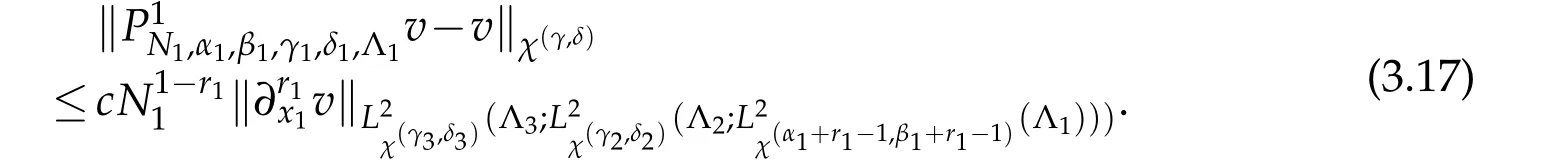
Using(2.2)withr=1,r=r2andr=r2?1 successively,we get that

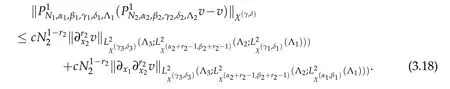
By using the same manner,we can deduce that

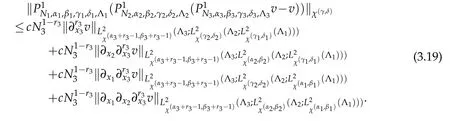
By substituting(3.17)-(3.19)into(3.16),we have that

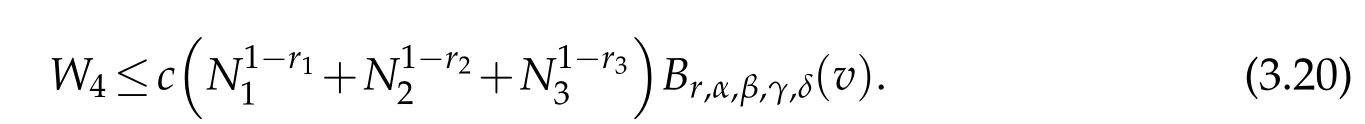
A combination of(3.13)-(3.15)and(3.20)leads to the desired the result(3.3).We next consider the case with(3.4).Clearly,

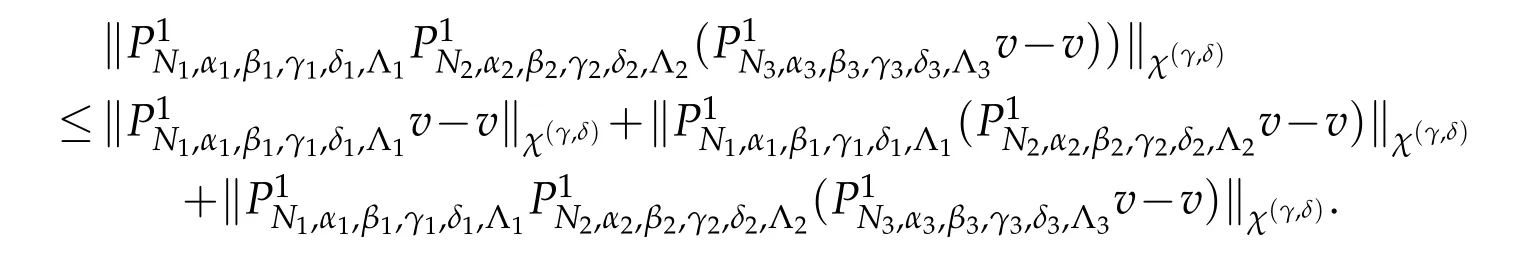
By(2.4)and the similar manner used above we can get(3.5)easily.

Obviously,forri=1,i=1,2,3,

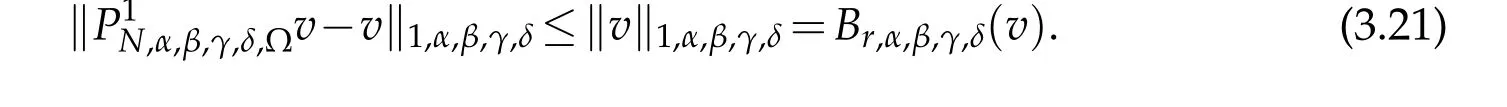
4 Jacobi-Gauss type interpolation in three dimensions

In this section,we study the Jacobi-Gauss type interpolation in three dimensions.Let Z=(Z1,Z2,Z3),Zq=G,R,L,q=1,2,3.The discrete inner product and norm in three dimensions are given by

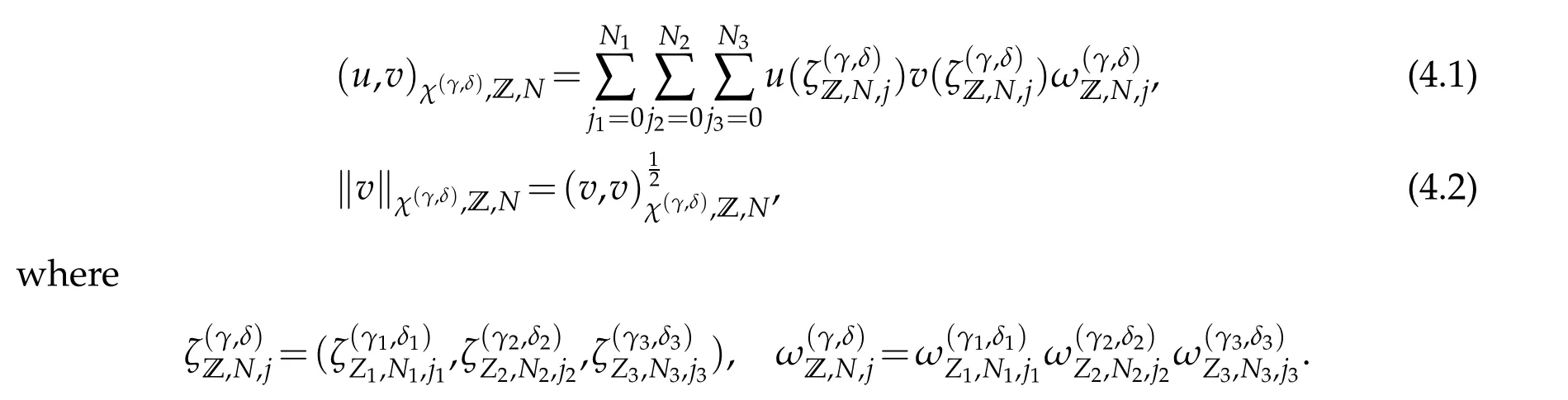
By the virtues of one-dimensional Jacobi discrete inner product,we have

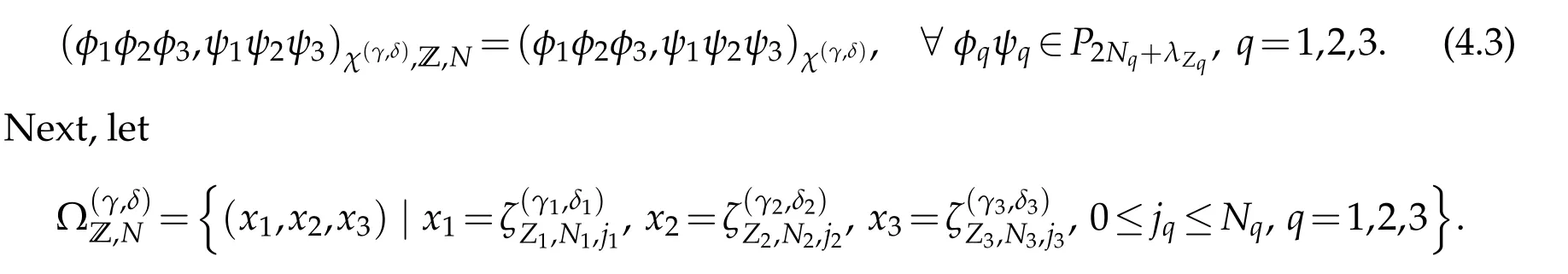
Let G=(G,G,G),the three dimensional Jacobi-Gauss-type interpolationIG,N,γ,δ,?v(x)∈PN(?),is determined uniquely by

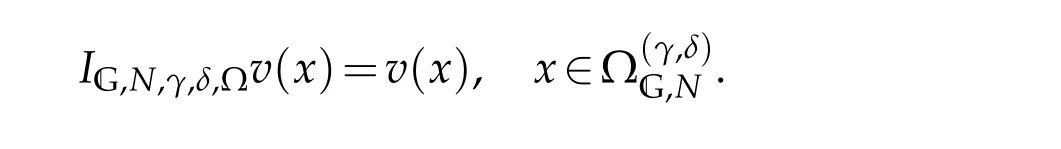
Letkq,lq∈N,q=1,2,3,k=(k1,k2,k3),l=(l1,l2,l3)and

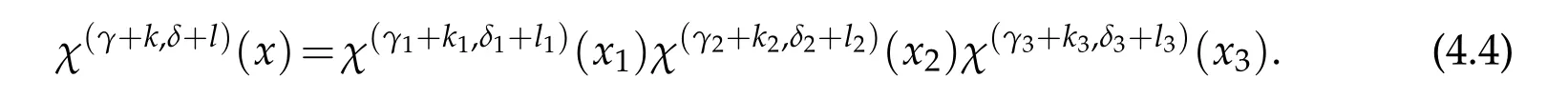
Now we introduce the non-isotropic spaces

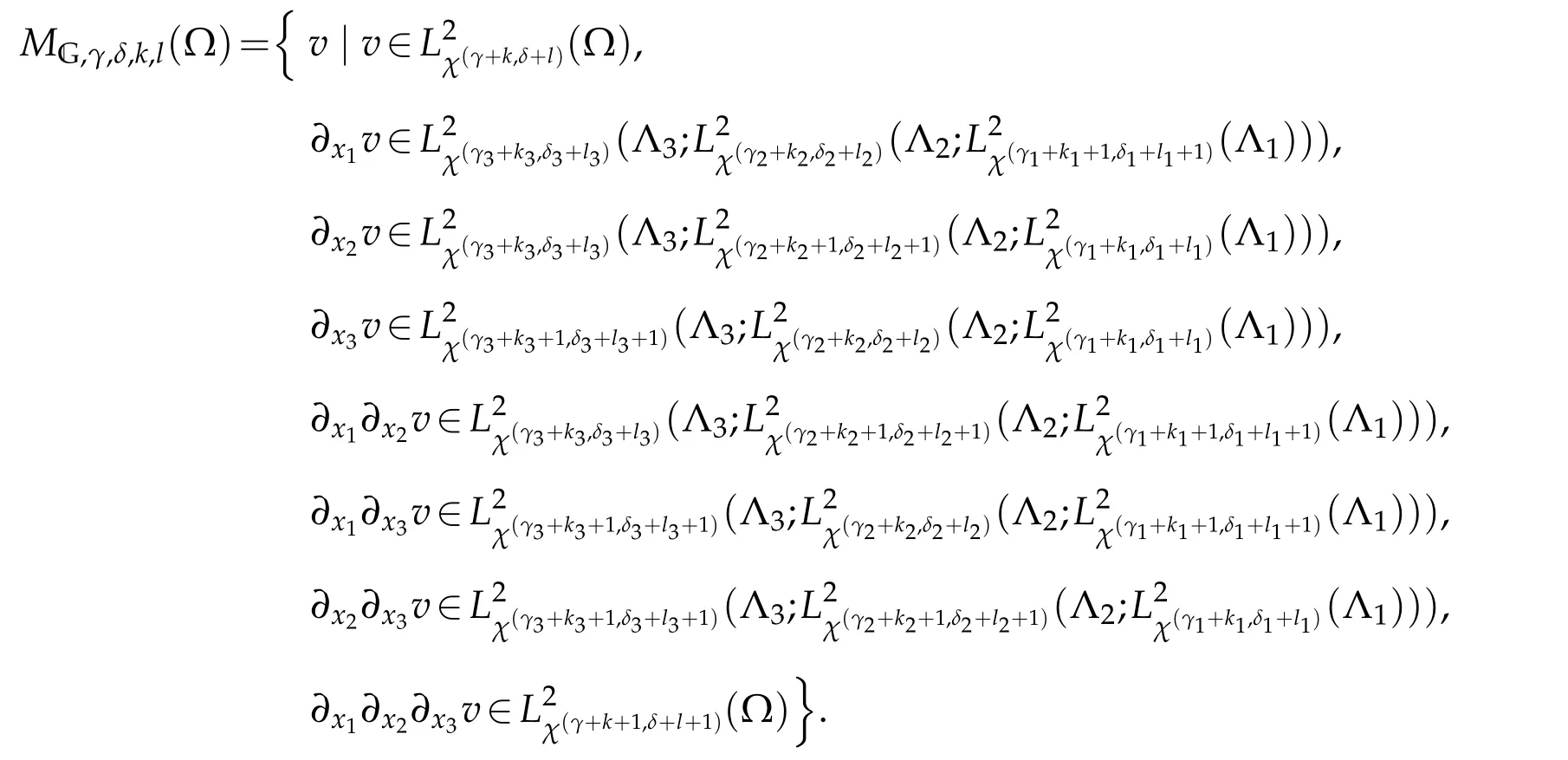
Equipped with the norm

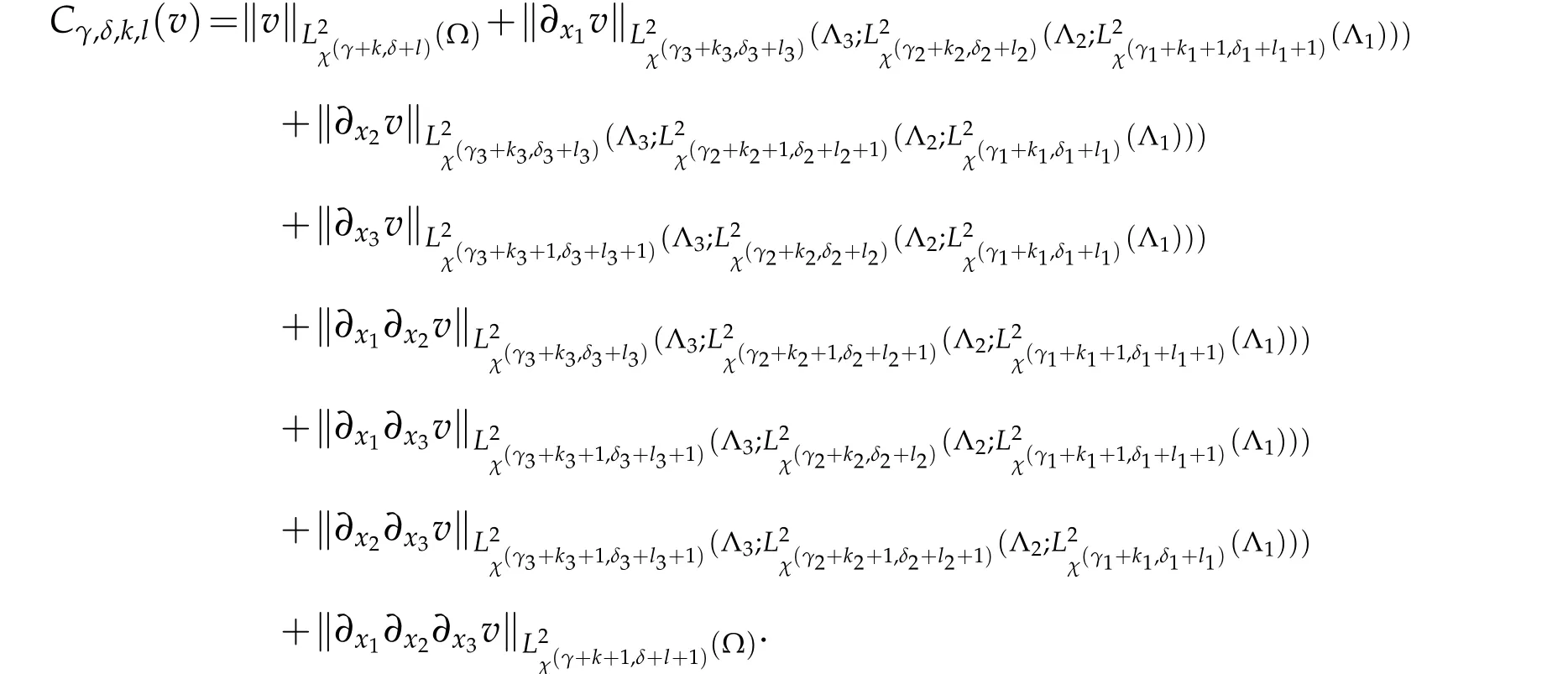
Theorem 4.1.For any v∈C(?)∩MG,γ,δ,k,l(?),kq,lq∈Nand0≤kq+lq≤1,q=1,2,3,

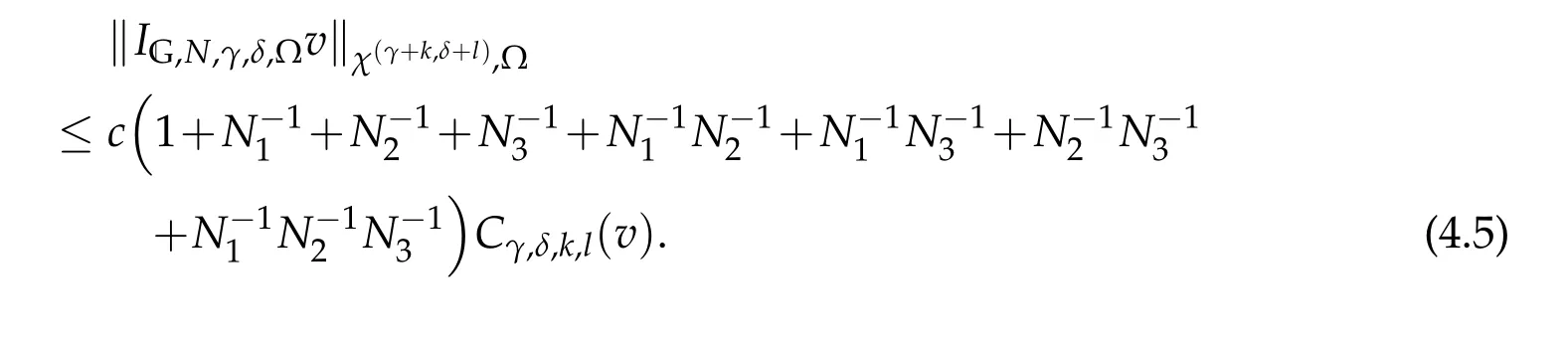
Proof.LetIG,Ni,γi,δi,Λibe the one-dimensional Jacobi-Gauss-type interpolation.Clearly,IG,N,γ,δ,?v=IG,N3,γ3,δ3,Λ3IG,N2,γ2,δ2,Λ2IG,N1,γ1,δ1,Λ1v.Due to(2.10),we can verify that

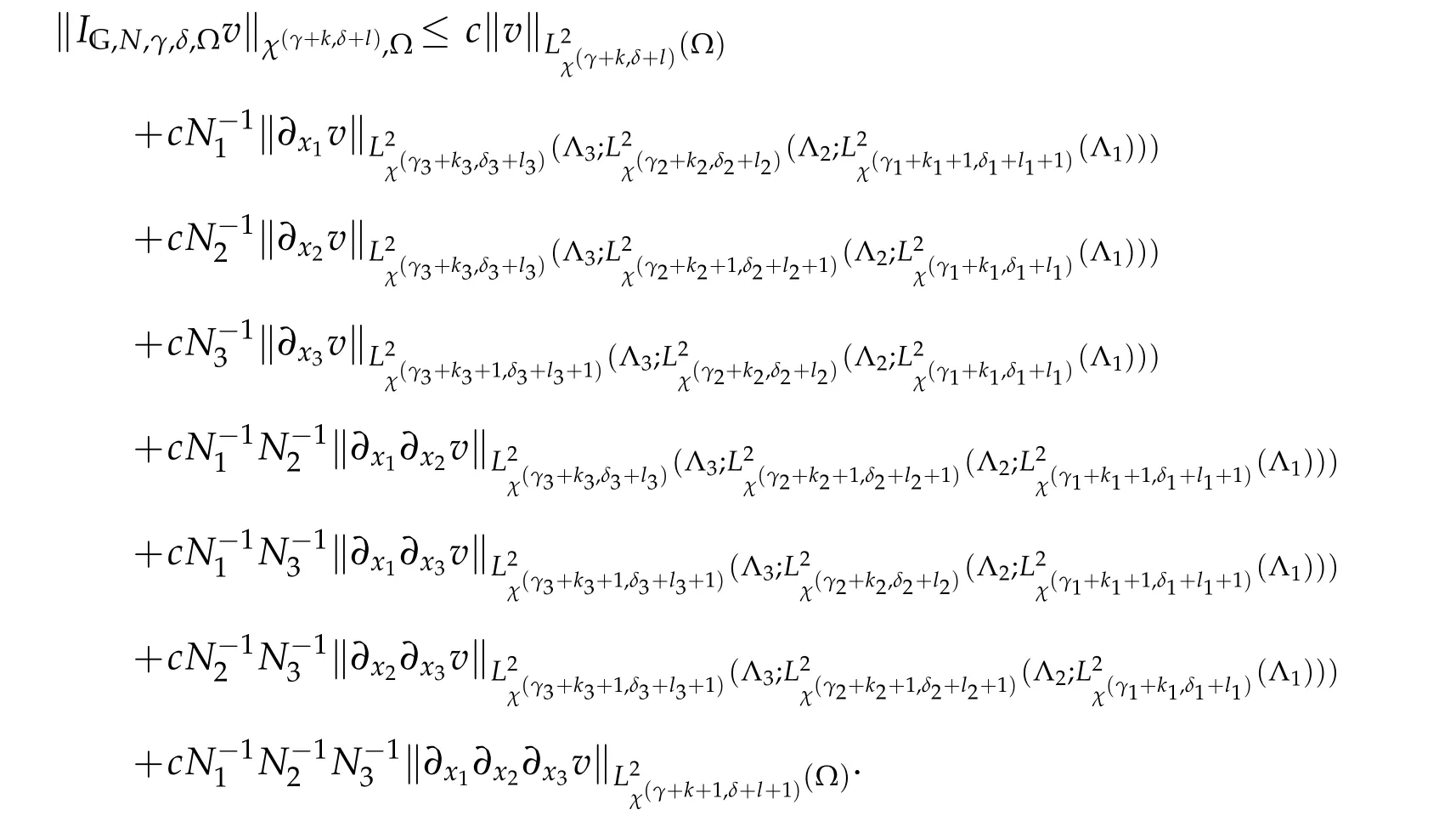
This leads to the desired result(4.5).

Remark 4.1.As to the Jacobi-Gauss-Radau interpolationIR,N,γ,δ,?vand the Jacobi-Gauss-Lobatto interpolationIL,N,γ,δ,?v,we can also define the spaces asMG,γ,δ,k,l(?)with the norms asCγ,δ,k,l(v),and using the same manner to get similar results as(4.5).

Next,we present the some results on the Jacobi-Gauss type interpolation.To do this,we introduce the non-isotropic spaces

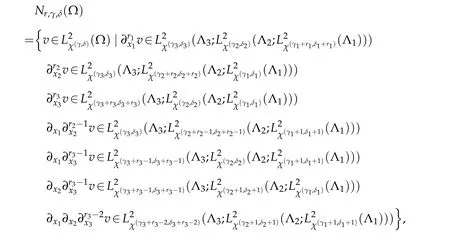
equipped with the semi-norm

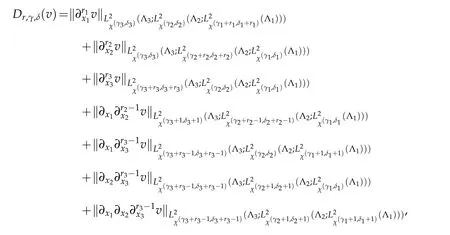
and the norm

Similarly,by using(2.10)and(2.13)we can get the following result.

Theorem 4.2.For any v∈C(?)∩Nr,γ,δ(?)and integer2≤ri≤Ni+1,i=1,2,3,then,

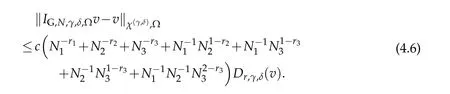
Remark 4.2.If in additionN1=O(N2)=O(N3)in Theorem 4.2,then result(4.6)can be written as

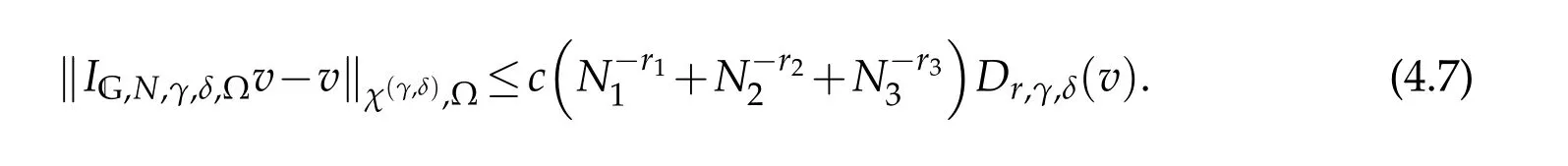
Moreover,as a specialcase we considerthe three-dimensionalLegendre-Gauss-Lobatto interpolation and related Bernstein-Jackson-type inequalities,which will be used in the sequel.

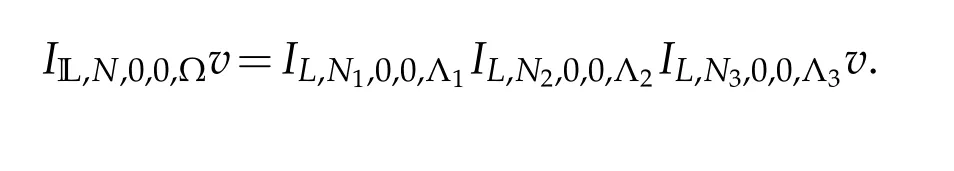
In order to describe the error of Legendre-Gauss-Lobatto interpolation we define the following quantity withri≥2,i=1,2,3.

Theorem 4.3.IfEr(v)is finite.Then for anyv∈C(?)and 2≤ri≤Ni+1,i=1,2,3,

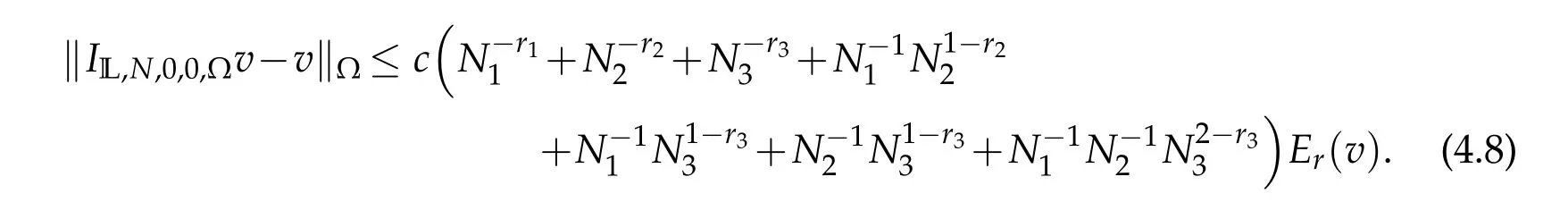
If in additionN1=O(N2)=O(N3),then

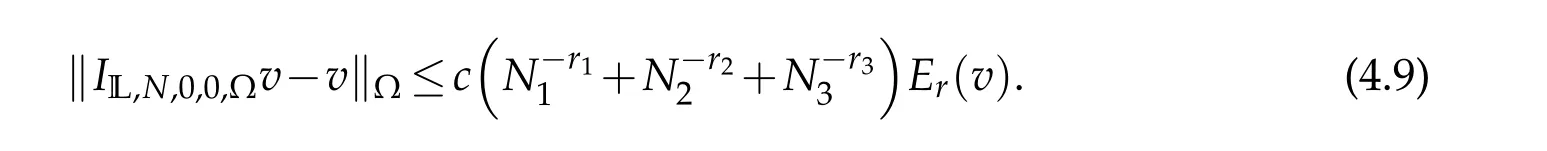
Proof.According to the definition ofIL,N,0,0,?,we have that

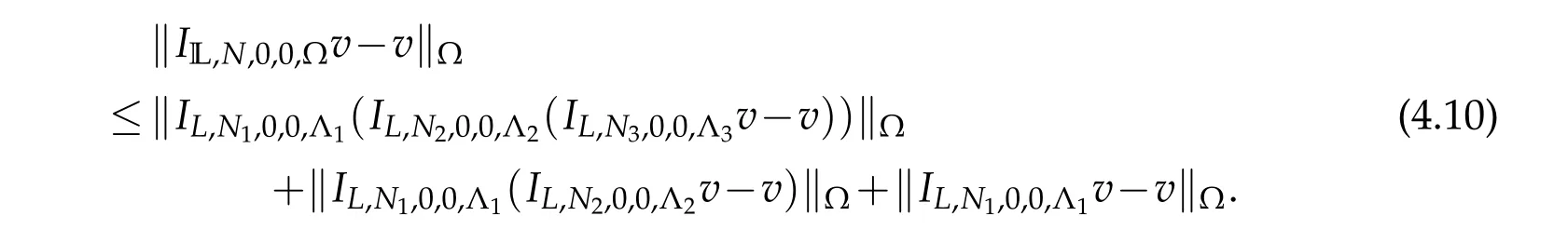
Due to(2.15)withα=β=0,we get that

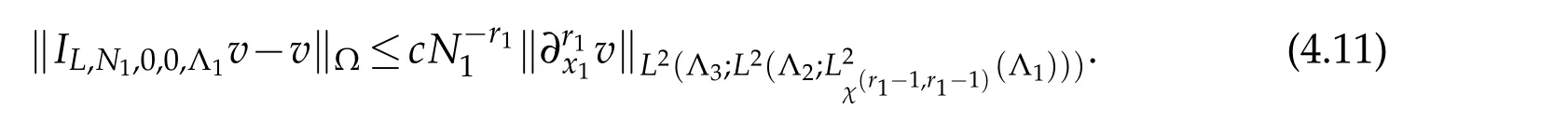
By using(2.16)and(2.15)withα=β=0,we derive that

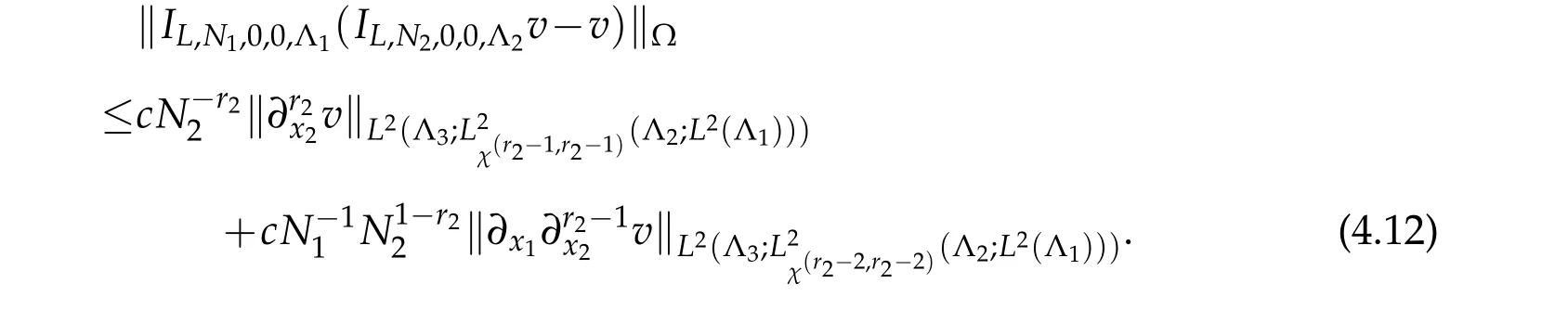
According to(2.18),(2.16)and(2.15)withα=β=0,we deduce that

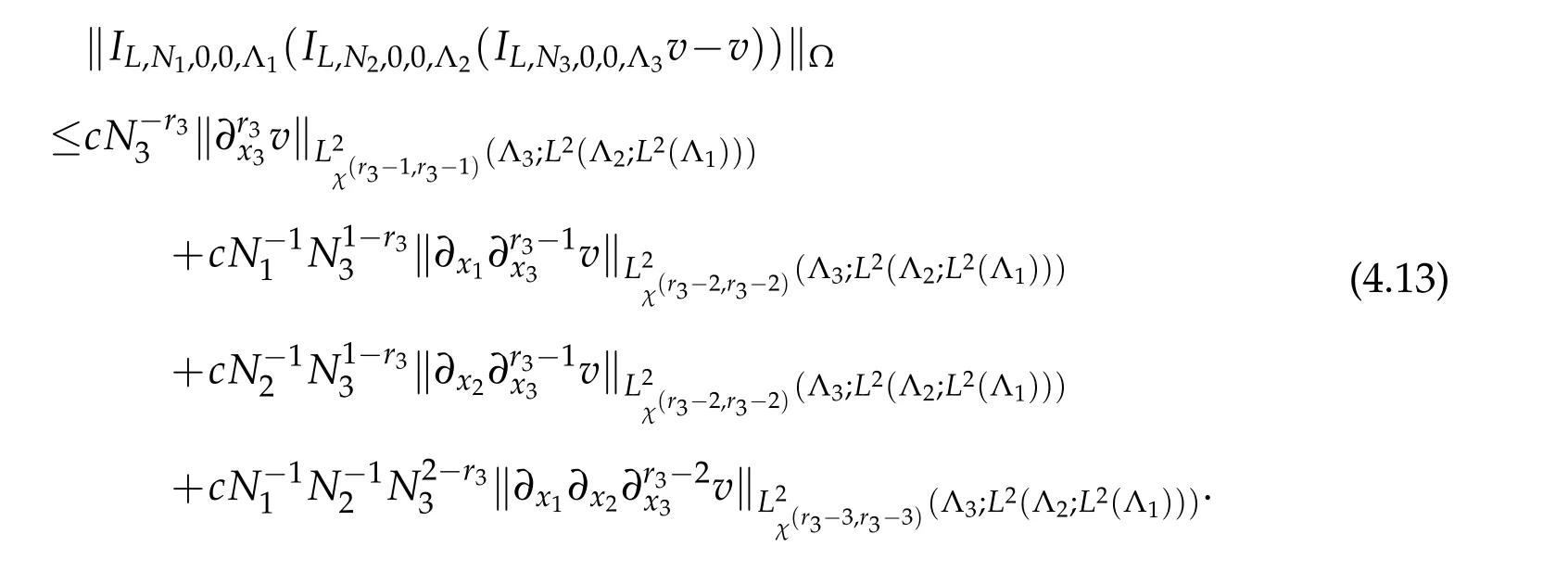
Substituting(4.11),(4.12)and(4.13)into(4.10)we get the desired result(4.8).IfN1=O(N2)=O(N3),the result(4.9)is clear.

Theorem 4.4.IfEr(v)is finite.Then for anyv∈C(?)and 2≤ri≤Ni+1,i=1,2,3,

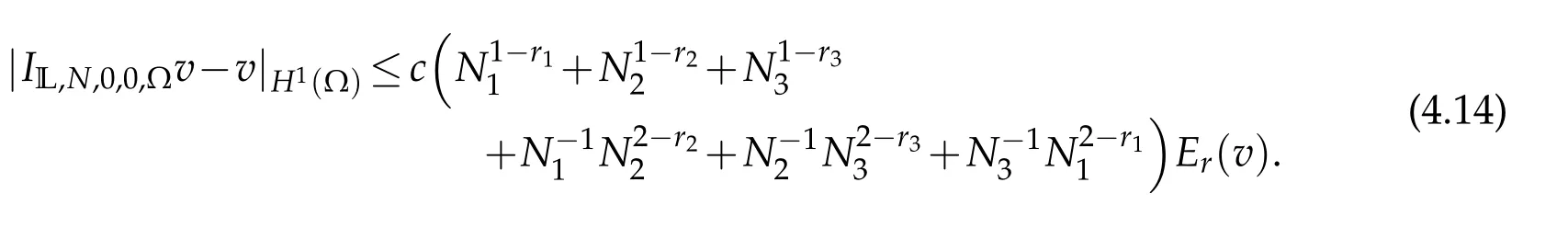
If in additionN1=O(N2)=O(N3),then

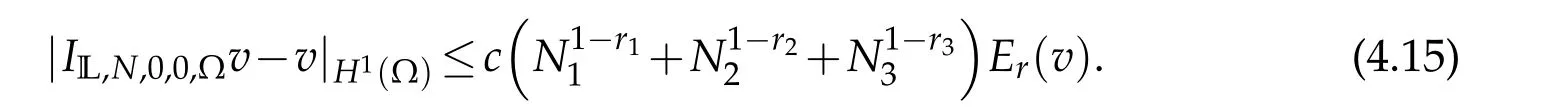
Proof.Obviously,

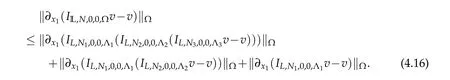
By(2.17),we have that

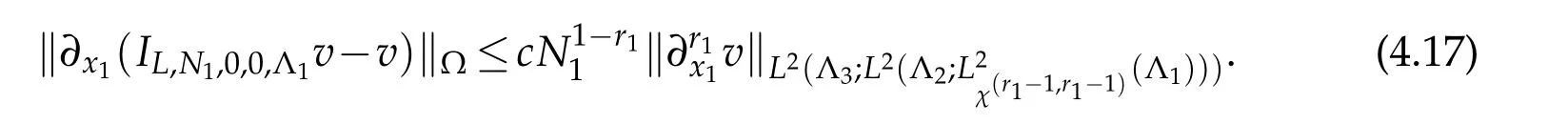
Thanks to(2.18)and(2.15),we deduce that

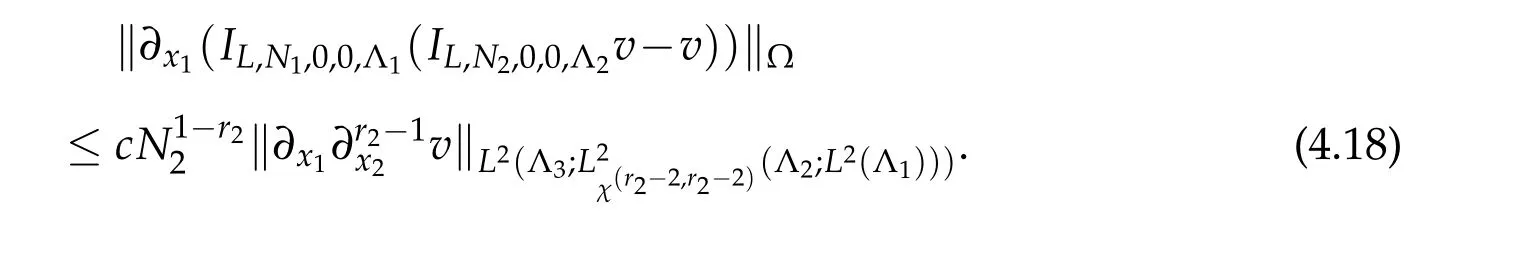
Using(2.18),(2.16)and(2.15)successively,we derive that

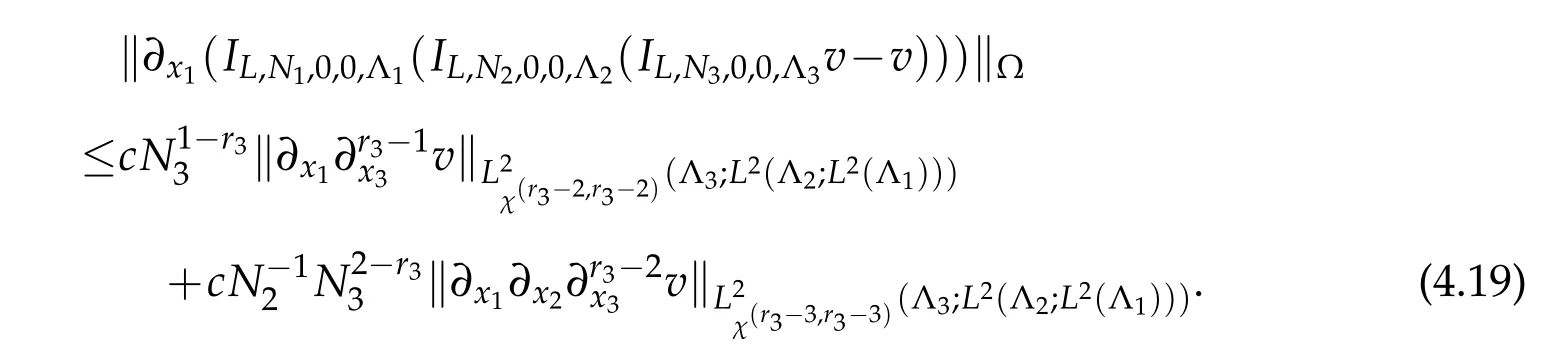
Substituting(4.17)-(4.19)into(4.16)yields

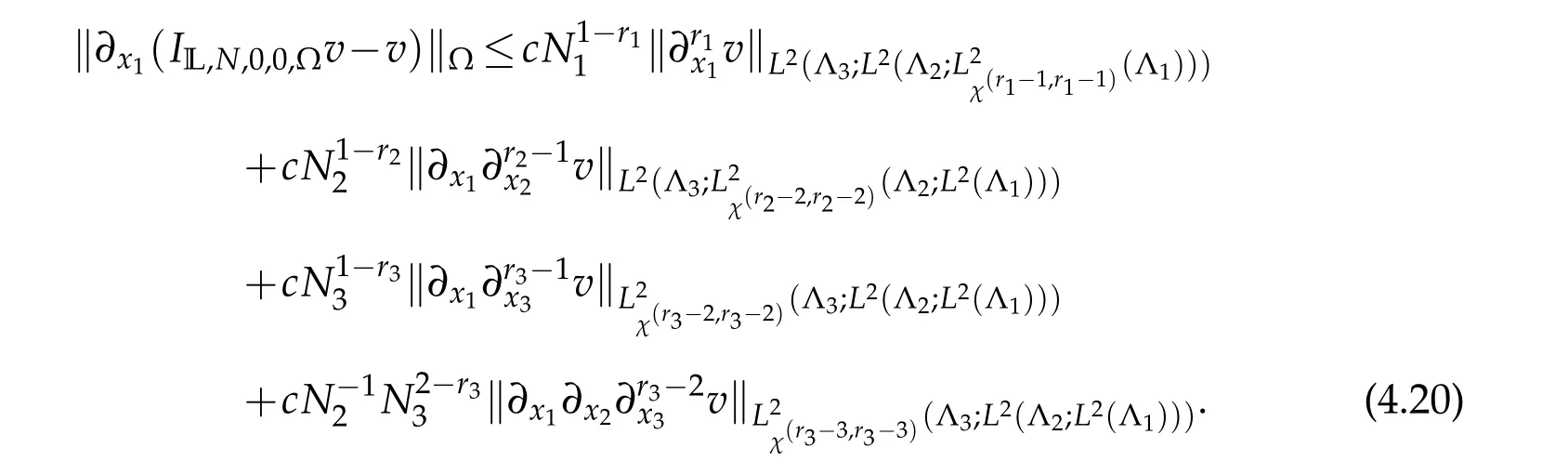
Similarly,we can get the following two estimates

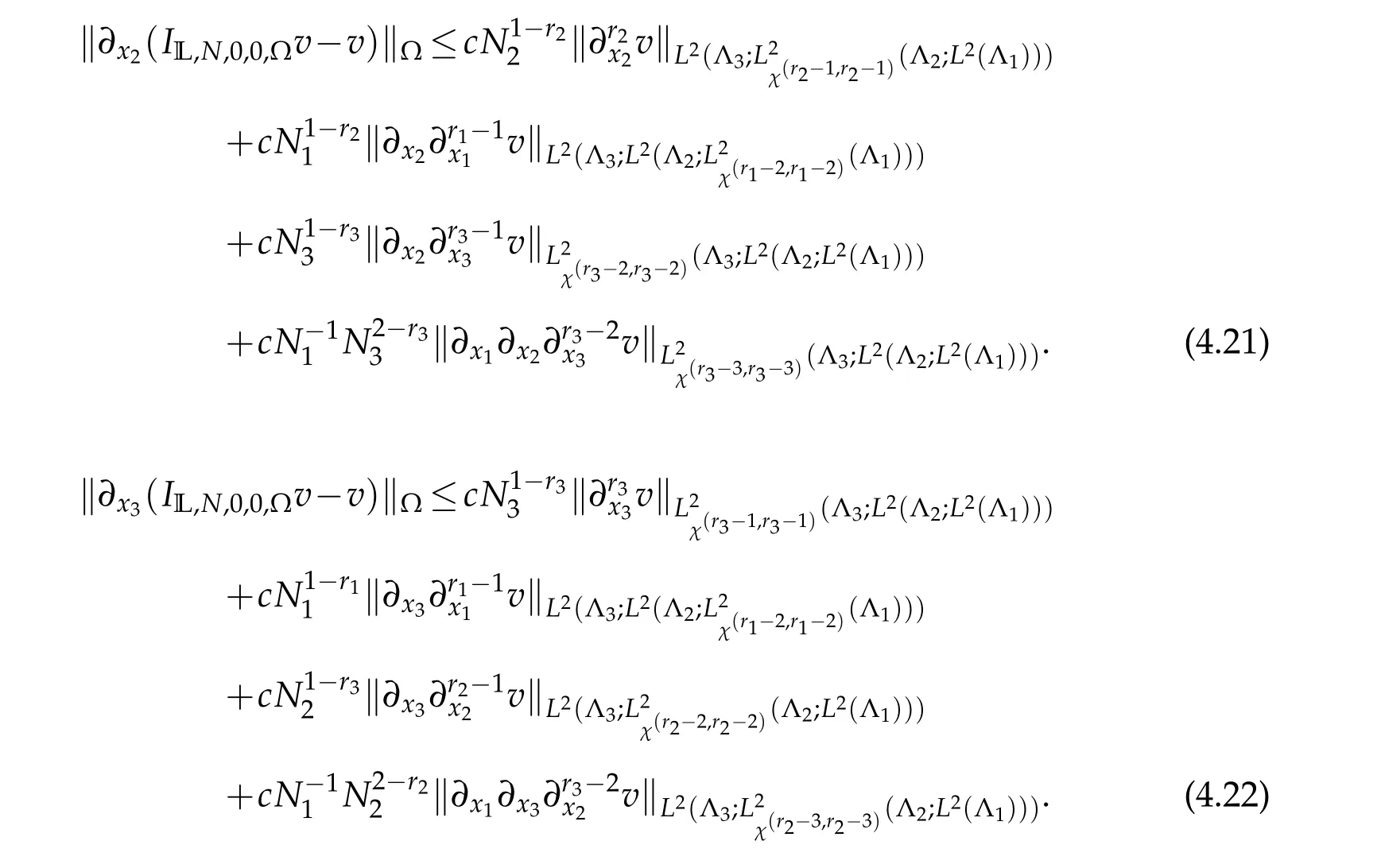
A combination of(4.20)-(4.22)leads to the desired result(4.14).This withN1=O(N2)=O(N3)implies(4.15).

Finally,we consider the Berstein-Jackson type inequality.Letη=(η1,η2,η3),0≤ηi≤12,i=1,2,3,andri＞2,i=1,2,3.We denote the quantity

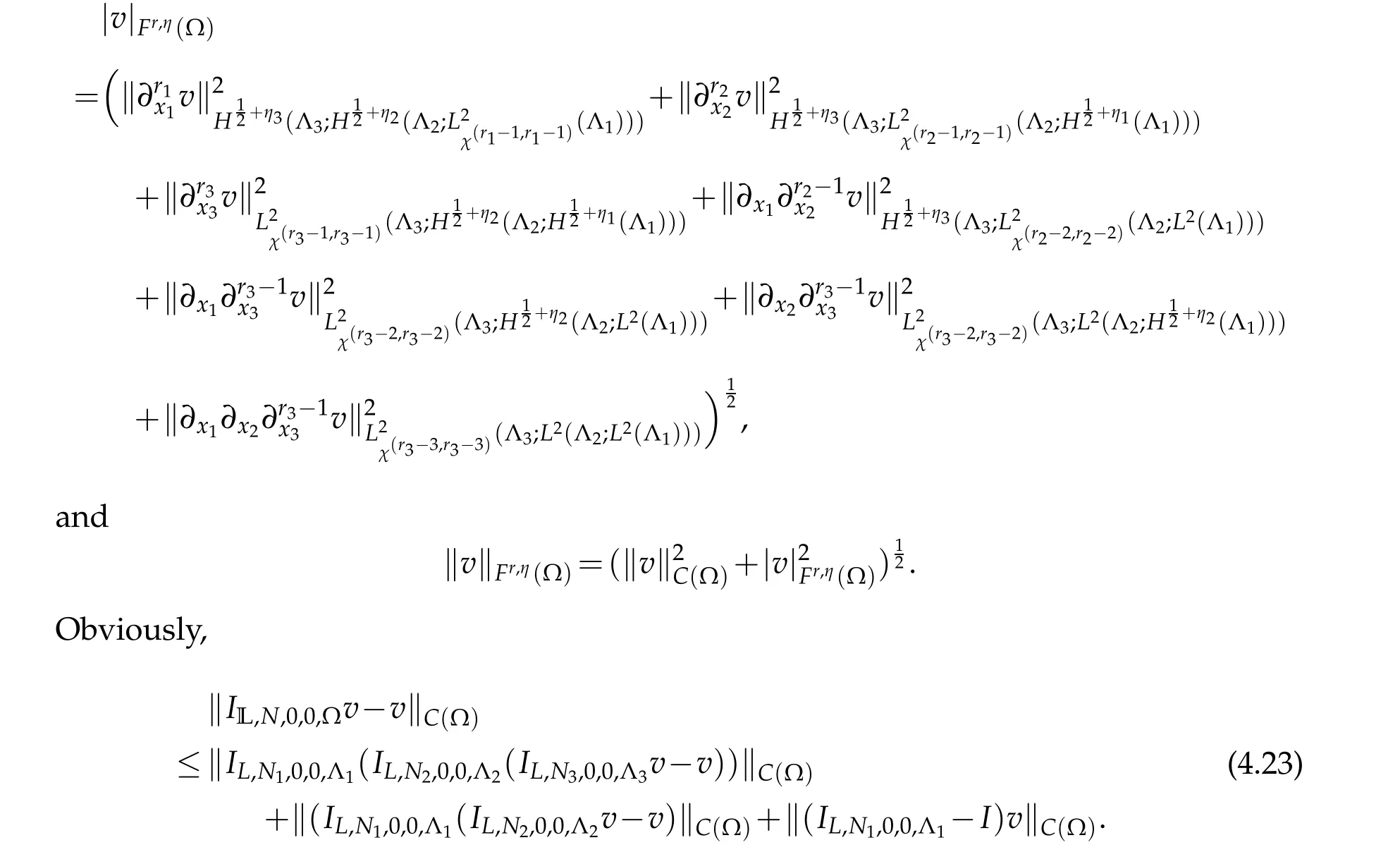
Thanks to(2.19)and the embedding inequality,we have that

According to(2.19)withr=1,r=r2,r=r2?1 successively,and the embedding inequality,we get that

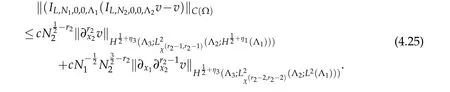
Using(2.19)withr=1 repeatedly,(2.19)withr=r3,r=r3?1 and the embedding inequality,

we derive that

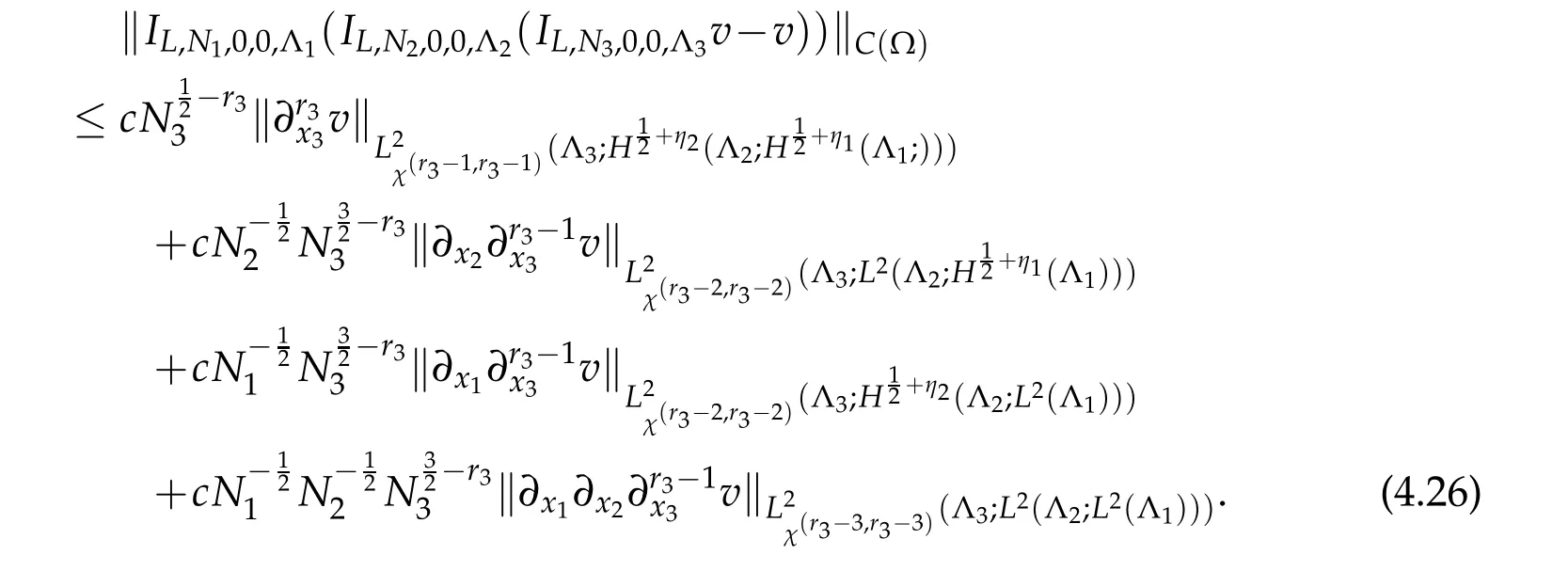
By substituting the above three inequalities into(4.23),we reach that

IfN1=O(N2)=O(N3),then the above estimation can be written as

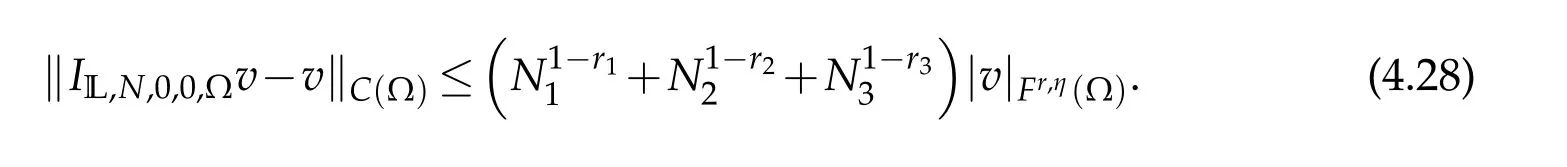
5 Jacobi method for three dimensional singular problem

This section is devoted to the Jacobi spectralmethod and the Jacobi pseudospectralmethod for three dimensional singular problem.Let

We consider the following model problem

Without losing generality,we suppose that

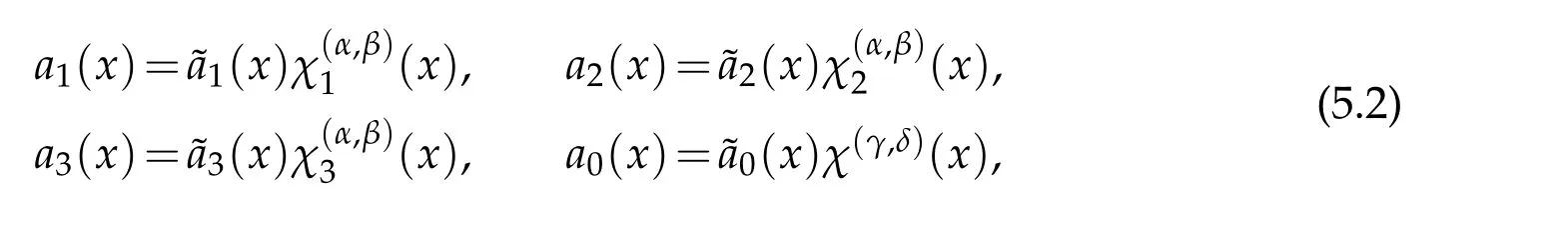
where

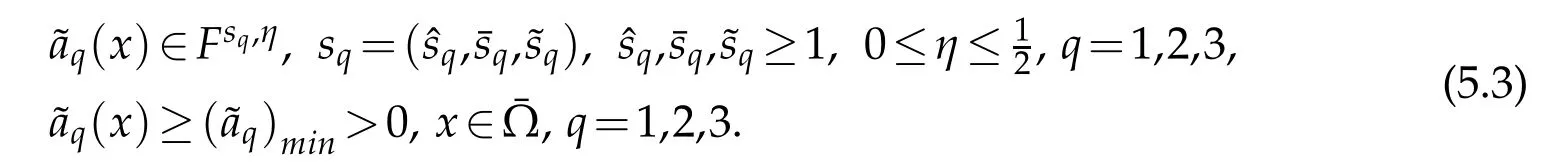
We look for singular solution of(5.1)such that

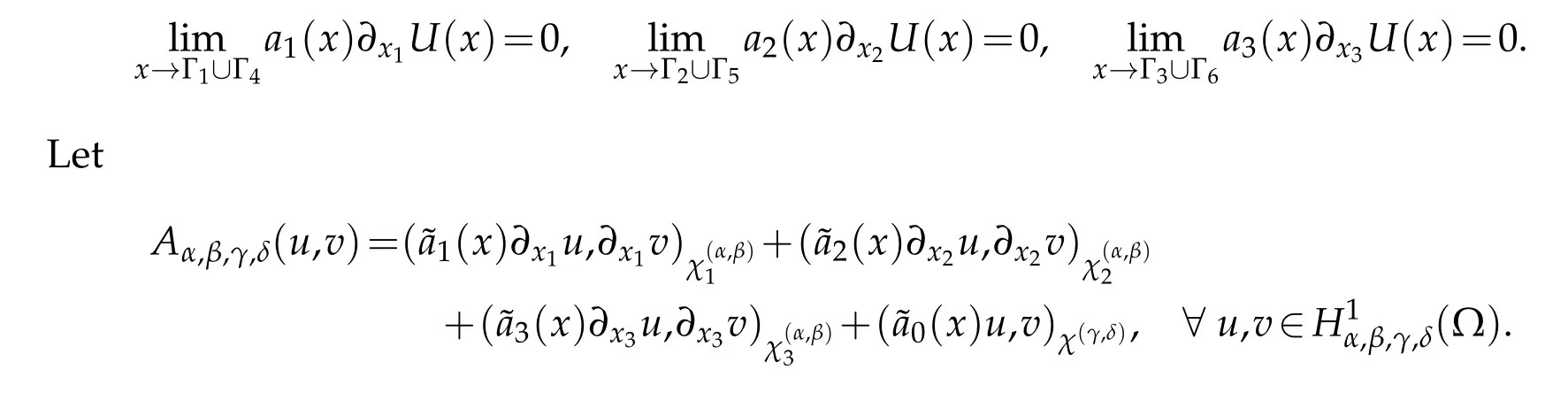
A weak formulation of(5.1)is to findU∈H1α,β,γ,δ(?)such that

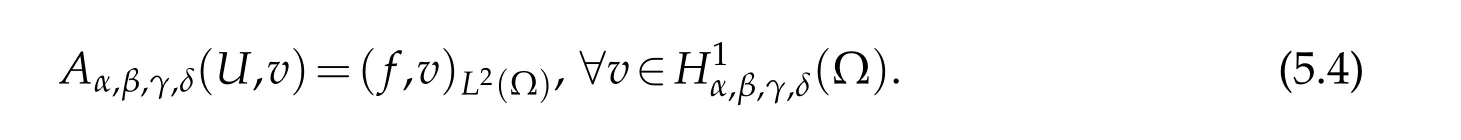
It can be verified that for anyu,v∈H1α,β,γ,δ(?),

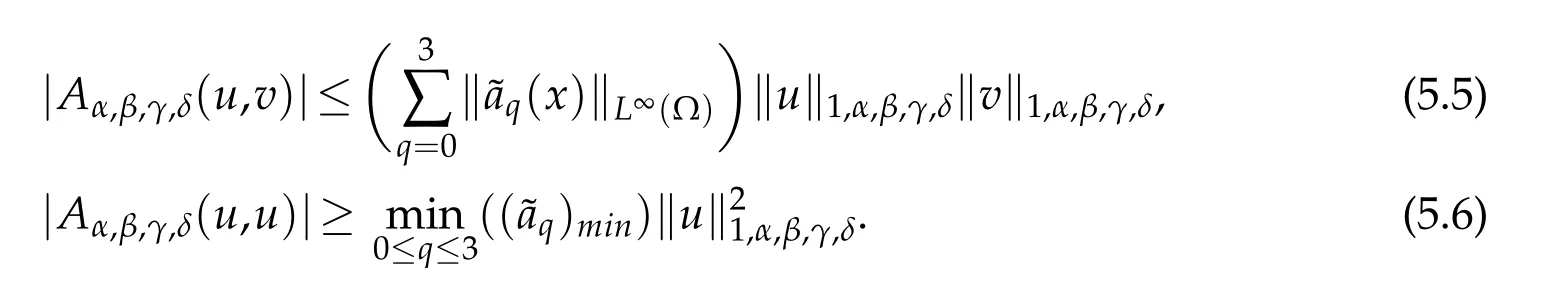
Now,letuN∈PN(?)be the approximation ofU,satisfying

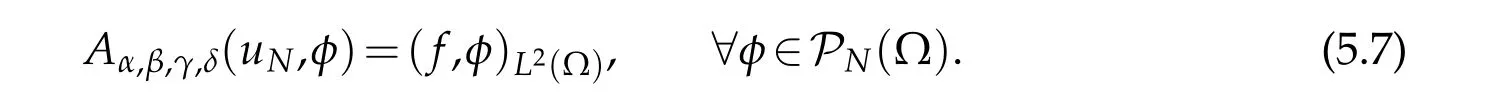
Due to(5.5)and(5.6),the solution ofequation(5.7)is unique and ‖uN‖1,α,β,γ,δ≤c‖f‖χ(?γ,?δ).

According to(5.4)and(5.7),we have that

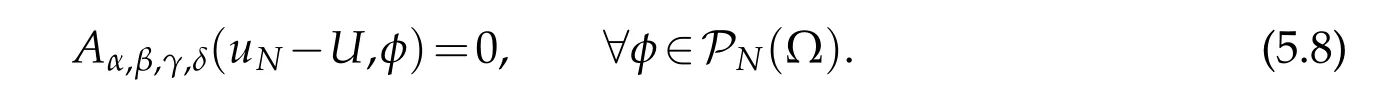
Theorem 5.1.If(3.1)and(5.2)hold,and Br,α,β,γ,δ(U)is finite,then for1≤ri≤Ni+1,i=1,2,3

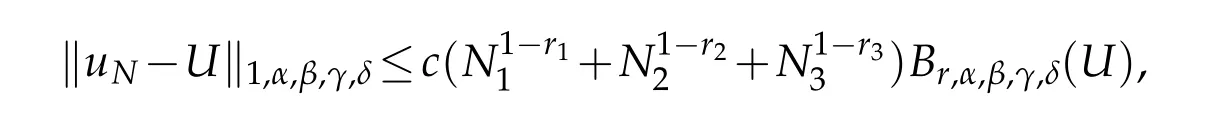
where the constant c depends only on the norms‖?ai‖C(?),i=0,1,2,3.

Proof.LetUN=P1N,α,β,γ,δ,?U.By using(5.6),(5.8)and Theorem 3.2 successively,we get that

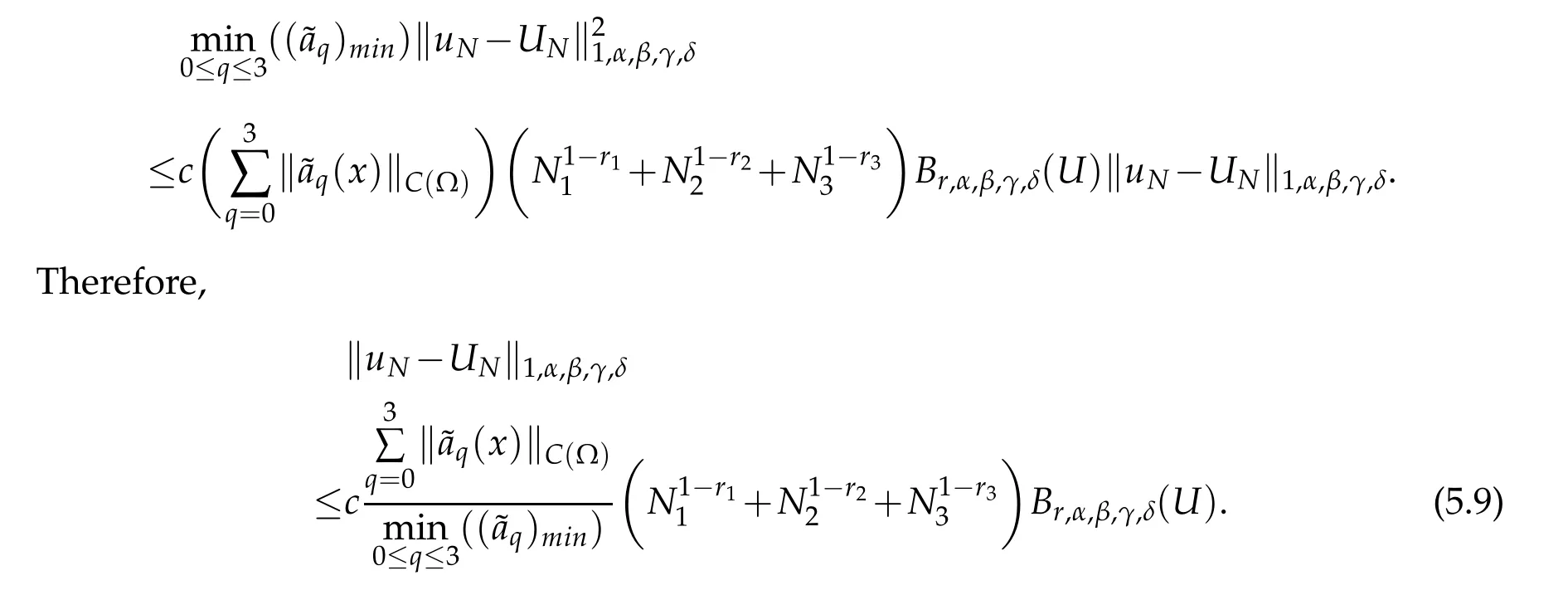
By using Theorem 3.2 and(5.9),we derive that

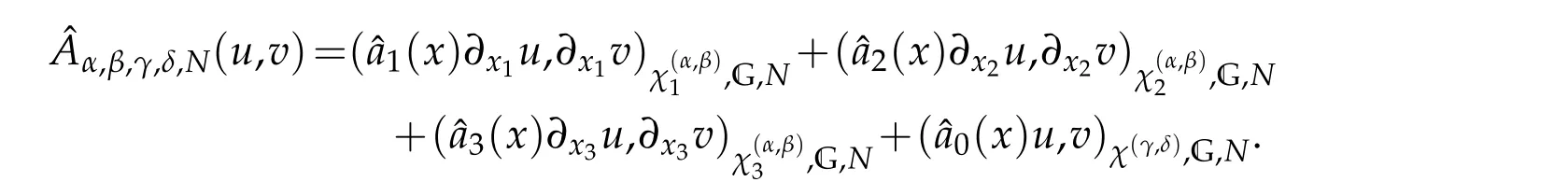
The Jacobi pseudospectral scheme of(5.1)is to finduN∈PN(?)such that

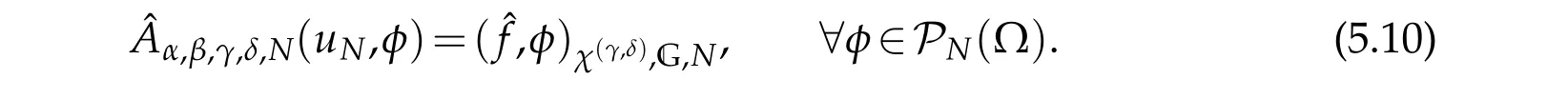
By(4.3),ifφ,ψ∈PN(?),we have that

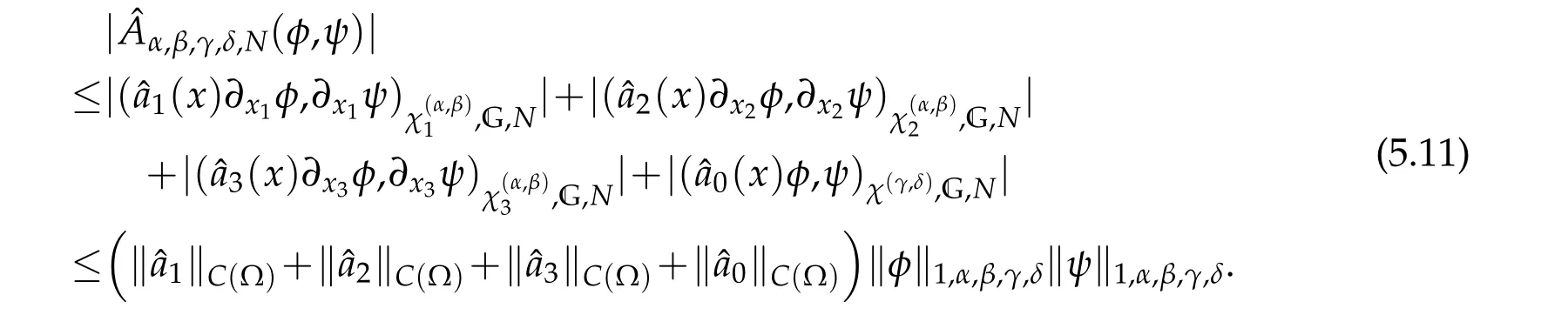
Thanks to(4.27)and(5.3),there exists a constantc?＞0,depending only on‖?aq‖F(xiàn)sq,1,q=0,1,2,3,such that

Therefore,for anyφ,ψ∈PN(?)

Besides,for anyφ∈ PN(?)and suitably largeN,according to(4.3),(4.27)and(5.3),the coefficient?aq(x),q=0,1,2,3,are uniformly bounded below by a constantc?＞0,

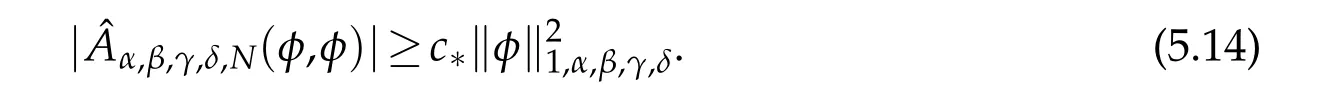
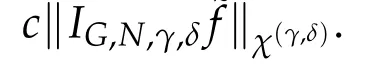
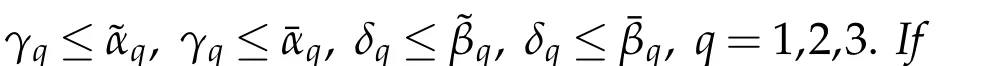
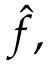
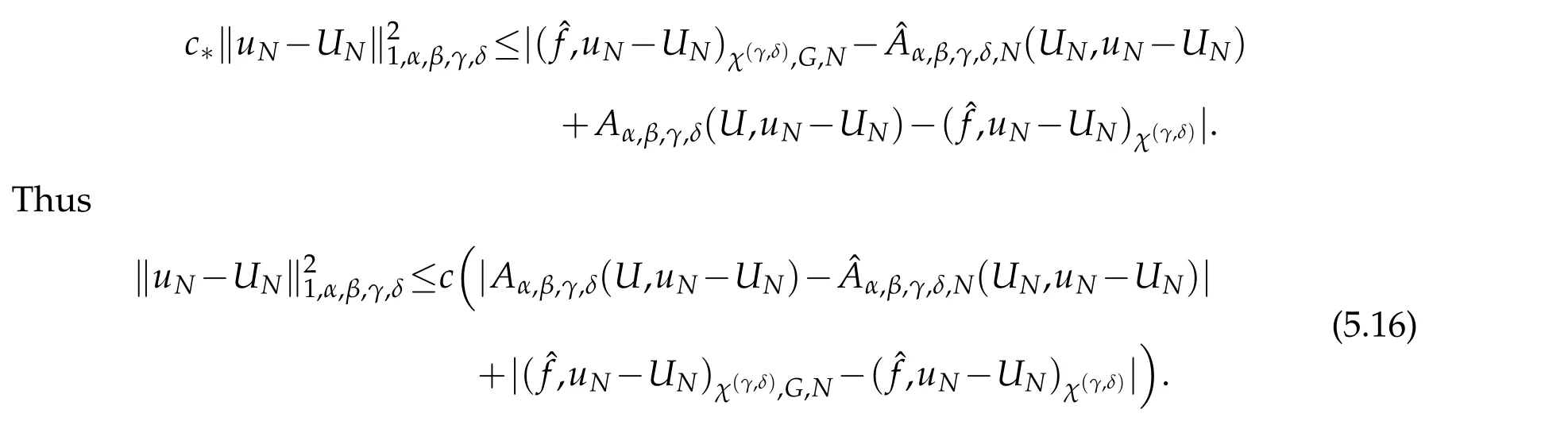
For simplicity,let

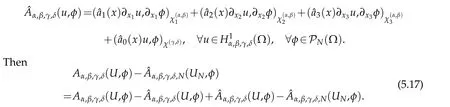
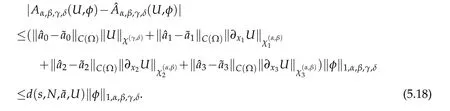
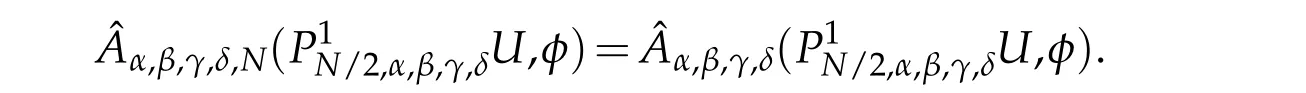
Thanks to the above equality,(5.5),(5.13)and(3.3),we have that

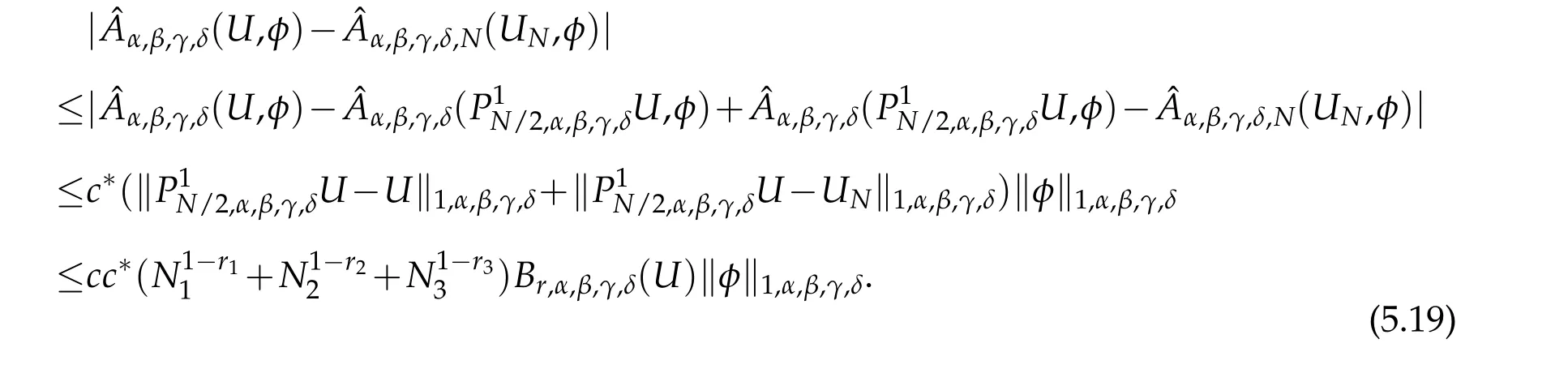
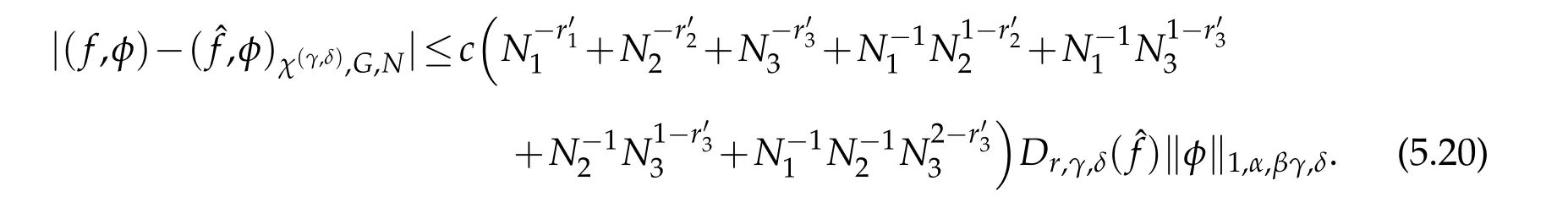
A combination of(5.16)-(5.20)withφ=uN?UN,and(3.3)leads to the desired result(5.15).

6 Numerical results

In this section,we present some numerical results to demonstrate the efficiency of the proposed methods.We consider the singular problem(5.1)with

Take the test function

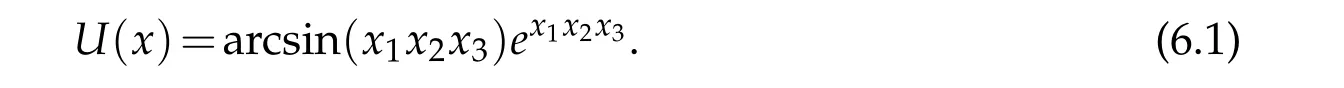
Clearly,|?xqU|→∞,q=1,2,3,asxtends to Γj∪Γj+3,1≤j≤3.

LetζG,Nq,jqandωG,Nq,jqbe nodes and weights of the one-dimensional Legendre-Gauss quadrature.We measure the error of the spectral method by

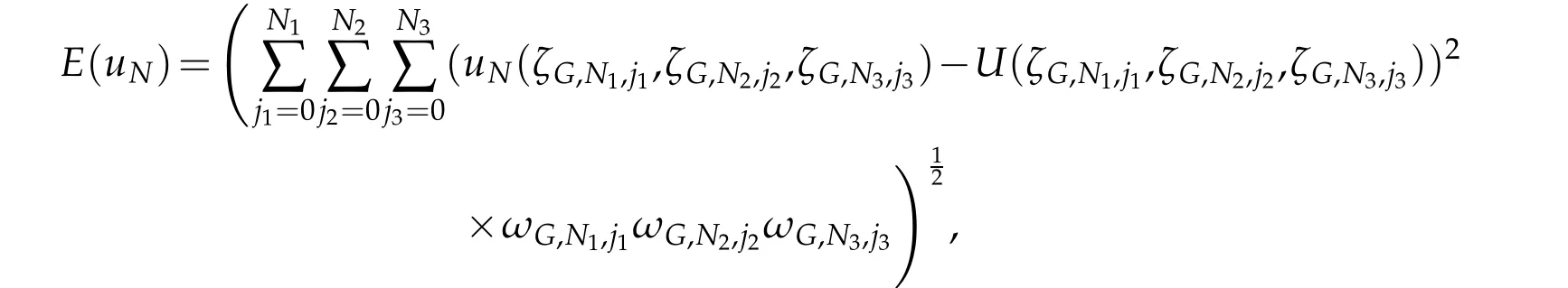
and the error of the pseudospectral method errors by

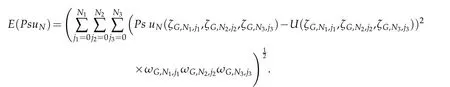
In table 1,we presentthe errorsE(uN)andE(PsuN)withN1=N2=N3=N.Obviously,the two schemes provide accurate numerical solutions,and the numerical solutions converge to the exact solution rapidly as N increases.This confirms the theoretical analysis well.

Table 1:Errors of spectral method and pseudospectral method

In Figs.1-3,we compare the exact solution and the numerical solution of(5.7)and(5.9)withN=32.Clearly,the numerical solutions of spectral scheme and pseudospectral scheme match the exact solution very well whenz=0.9,0,?0.9,respectively.

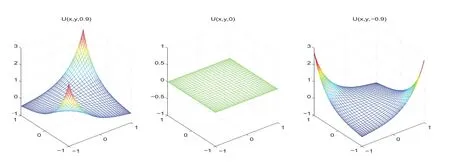
Figure 1:Exact solutions

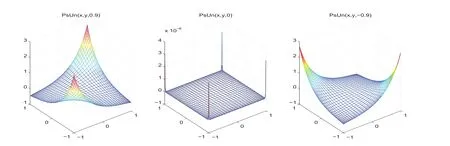
Figure 3:Solutions of pseudospectral scheme

7 Concluding Remarks

In this paper,we establish some basic results on the Non-isotropic 3-dimensional Jacobi spectral approximation and Jacobi-Gauss type interpolation,with which the convergence of proposed schemes are proved.These results play important role in designing and analyzing Jacobi spectral methods and pseudospectral methods for various practical problems.As examples,we consider a singular problem in three dimensions.The numerical results demonstrate the spectral accuracy of proposed schemes,and agreed well with the theoretical analysis.

We also derive a series of sharp results on the Legendre-Gauss type interpolation and the related Bernstein-Jackson type inequalities in three dimensions,which improve and generalize the existing results.They are very useful for pseudospectralmethod of partial differential equations with non-constant coefficients,as well as numerical solutions of initial value problems of nonlinear ordinary differential equations.

Acknowledgments

The first author is supported in part by NSFC grants N.11171227 and N.11371123,Fund for Doctoral Authority of China N.20123127110001,NSF of Shanghai N.13ZR1429800,and the State Scholarship Fund of China N.201308310188.

The third author is supported in part by NSF of China N.11171227,Fund for Doctoral Authority of China N.20123127110001,Fund for E-institute of Shanghai Universities N.E03004,Leading Academic Discipline Project of Shanghai Municipal Education Commission N.J50101.

[1]I.Babuˇska and B.Guo.Direct and inverse approximation theorems for the p.version of the if nite element method in the framework of weighted Besov spaces,Part I:Approximability of functions in the weighted Besov spaces.SIAM J.Numer.Anal.,39(5):1512–1538,2001.

[2]C.Bernardi,M.Dauge and Y.Maday.Spectral Methods for Axisymmetric Domains.Series in Applied Mathematics,3,1999.

[3]C.Bernardi and Y.Maday.Spectral Methods.Handbook of Numerical Analysis,Techniques of Scientific Computing,5:209–486,1997.

[4]J.P.Boyd.Orthogonal rational functions on a semi-infinite interval.J.Comp.Phys.,70:63–88,1987.

[5]J.P.Boyd.Spectral methods using rational basis functions on an infinite interval.J.Comput.Phys.,69:112–142,1987.

[6]J.P.Boyd.Chebyshev and Fourier Spectral Methods.2’nd edition,Dover Publication Inc.,Mineda,New York,2001.

[7]C.Canuto,M.Y.Hussaini,A.Quarteroni and T.A.Zang.Spectral Methods in Fluid Dynamics,Springer-Verlag,Berlin,1988.

[8]C.Canuto,M.Y.Hussaini,A.Quarteroni and T.A.Zang.SpectralMethods.Springer-Verlag,Berlin,2006.

[9]C.Canuto,M.Y.Hussaini,A.Quarteroni and T.A.Zang.Spectral Methods:Evolution to complex Geometries and Applications to Fluid Dynamics.Springer-Verlag,Berlin,2007.

[10]C.I.Christov.A complete orthogonal system of functions inL2(?∞,∞)space.SIAMJ.Appl.Math.,42:1337-1344,1982.

[11]D.Funaro.Polynomial Approximations of Differential Equations.Springer-Verlag,Berlin,1992.

[12]D.Gottlieb and S.A.Orszag.Numerical Analysis of Spectral Methods:Theory and Applications.SIAM-CBMS,Philadephia,1997.

[13]B.-Y.Guo.Spectral method and Their Applications.World Scientific,Singapore,1998.

[14]B.-Y.Guo.Gegenbauer approximation and its applications to differential equations on the whole line.J.Math.Anal.Appl.,226:180-206,1998.

[15]B.-Y.Guo.Jacobi spectral approximations to differential equations on the half line.J.Comp.Math.,18:95-112,2000.

[16]B.-Y.Guo.Gegenbauer approximation in certain Hilbert spaces and its applications to singular differential equations.SIAM J.Numer.Anal.,37:621-645,2000.

[17]B.-Y.Guo.Jacobi approximations in certain Hilbert spaces and their applications to singular differential equations.J.Math.Anal.Appl.,243:373-408,2000.

[18]B.-Y.Guo.Gegenbauer approximation and its applications to differential equations with rough asymptotic behaviors at infinity.Appl.Numer.Math.,38:403-425,2001.

[19]B.-Y.Guo.Jacobispectralmethod fordifferentialequations with rough asymptotic behaviors at infinity.J.Comp.Math.Appl.,46:95-104,2003.

[20]B.-Y.Guo,J.Shen and L.-L Wang.Optimal spectral-Galerkin methods using generalized Jacobi polynomials.J.Sci.Comp.,27:305-322,2006.

[21]B.-Y.Guo,J.Shen and Z.-Q Wang.A rational approximation and its applications to differential equations on the half line.J.Sci.Comp.,15:117-148,2000.

[22]B.-Y.Guo,J.Shen and Z.-Q.Wang.Chebyshev rational spectral and pseudospectralmethods on a semi-infinite interval.Int.J.Numer.Meth.Eng.,53:65-84,2002.

[23]B.-Y.Guo,T.Sun and C.Zhang.Jacobi and Laguerre quasi-orthogonal approximations and related interpolations.Math.Comp.,82:413-441,2013.

[24]B.-Y.Guo and L.-L.Wang.Jacobi interpolation approximations and their applications to singular differential equations.Adv.Comput.Math.,14:227-276,2001.

[25]B.-Y.Guo and L.-L.Wang.Non-isotropic Jacobi spectral method.Cont.Math.,329:157-164,2003.

[26]B.-Y.Guo and L.-L.Wang.Jacobi approximations in non-uniformly Jacobi-weighted Soblev spaces.J.Appro.Theo.,128:1-41,2004.

[27]B.-Y.Guo and Z.-Q.Wang.Modified Chebyshev rational spectral method for the whole line.Discrete and Continuous Dynamical System,Supplement Volume,365-374,2003.

[28]B.-Y.Guo and Z.-Q.Wang.Legendre rational approximation on the whole line.Science in China,Ser.A,Mathematics,47:155-164,2004.

[29]B.-Y.Guo and K.-J.Zhang.On non-isotropic Jacobi pseudospectral method.J.of Comput.Math.,26:2008,511-535.

[30]A.Quarteroni.Some results of Bernstein and Jackson type for polynomial approximation inLpspace.Japan J.Appl.Math.,1:173-181,1984.

[31]L.-L.Wang and B.-Y.Guo.Mixed Fourier-Jacobi spectral method.J.Math.Anal.Appl.,315:8-28,2006.

[32]Z.-Q.Wang and B.-Y.Guo.A rational approximation and its application to nonlinear differential equations on the whole line.J.Math.Anal.Appl.,247:374-403,2002.

17 October,2014;Accepted 2 Januray,2015

?Corresponding author.Email addresses:yj-jiao@shnu.edu.cn(Y.J.Jiao),615948173@qq.com(S.Chen),byguo@shnu.edu.cn(B.Y.Guo).