李 影,宋衛(wèi)東

(安徽師范大學 數(shù)學計算機科學學院,安徽 蕪湖 241003)

?

研究簡報

局部對稱偽Riemann流形中的緊致極大類時子流形

李 影,宋衛(wèi)東

(安徽師范大學 數(shù)學計算機科學學院,安徽 蕪湖 241003)

利用活動標架法,得到了局部對稱偽Riemann流形中極大類時子流形的一個Simons型積分不等式,以及該子流形成為全測地類時子流形的關(guān)于其第二基本形式模長平方的拼擠定理.

偽Riemann流形;局部對稱;極大類時子流形;全測地類時子流形

本文約定各類指標取值范圍如下:

1≤A,B,C,…≤n+p; 1≤i,j,k,…≤n;n+1≤α,β,γ,…≤n+p.

(1)

(2)

則有

(3)

(4)

類似地,曲率張量場Kαijk的共變導數(shù)Kαijk,l定義為

限制到Mn上時,有

(5)

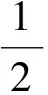
(1-δ),A≠B;

(1-δ),A,B,C,D互不相同.

(6)

再由式(1),(2),(5),(6)得

(7)

(8)

(9)

(10)

由于(tr(HαHβ))p×p是實對稱矩陣,因此選取法標架場{eα}可使之對角化,即

(11)

從而有

(12)

從而

(13)

由文獻[10]，顯然有

(14)

由式(7)～(14),有

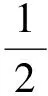
(15)

由于Mn是緊致無邊的,根據(jù)Stocks定理,對式(15)兩邊積分得

證畢.

(16)

證明:由已知條件式(16)可知式(15)的右邊非負,而Mn是緊致無邊的,由Hopf極大值原理可知S為常數(shù).從而式(15)左邊為零.因此,式(15)右邊也為零,即

結(jié)合已知條件可知S=0,故Mn是全測地類時子流形.證畢.

[1] 孔令令,裴東河.四維Minkowski空間中類時超曲面的de Sitter Gauss映射的奇點分類 [J].中國科學A輯：數(shù)學,2007,37(6):751-758.(KONG Lingling,PEI Donghe.Singularities of de Sitter Gauss Map of Timelike Hypersurface in Minkowski 4-Space [J].Science in China Series A：Mathematics,2007,37(6):751-758.)

[2] 沈一兵.關(guān)于偽Riemmann流形的極大子流形 [J].杭州大學學報:自然科學版,1991,18(4):371-376.(SHEN Yibing.On Maximal Submanifolds in Pseudo-Riemanian Manifolds [J].Journal of Hangzhou University:Natural Science,1991,18(4):371-376.)

[3] 胡有婧,紀永強.de Sitter空間中的緊致極大類時子流形 [J].吉林大學學報:理學版,2014,52(5):895-900.(HU Youjing,JI Yongqiang.The Compact Timelike Submanifolds in the de Sitter Space [J].Journal of Jilin University:Science Edition,2014,52(5):895-900.)

[4] 胡有婧,紀永強,汪文帥.局部對稱空間中的緊致子流形 [J].數(shù)學雜志,2013,33(6):1133-1144.(HU Youjing,JI Yongqiang,WANG Wenshuai.The Compact Submanifold in a Locally-Symmetric Space [J].Journal of Mathematics,2013,33(6):1133-1144.)

[5] 白正國,沈一兵,水乃翔,等.黎曼幾何初步 [M].北京:高等教育出版社,2004.(BAI Zhengguo,SHEN Yibing,SHUI Naixiang,et al.An Introduction to Riemann Geometry [M].Beijing:Higher Education Press,2004.)

[6] 紀永強.子流形幾何 [M].北京:科學出版社,2004.(JI Yongqiang.Geometry of Submanifolds [M].Beijing:Science Press,2004.)

[7] 宋衛(wèi)東,江桔麗.關(guān)于局部對稱偽黎曼流形中的2-調(diào)和類空子流形 [J].系統(tǒng)科學與數(shù)學,2007,27(2):170-176.(SONG Weidong,JIANG Juli.On 2-Harmonic Space-Like Submanifolds of a Locally Symmetric Preudo-Riemannian Manifold [J].Journal of Mathematics and System Science,2007,27(2):170-176.)

[8] Goldberg S L.Curvature and Homology [M].London:Academic Press,1962.

[9] 宋衛(wèi)東.關(guān)于局部對稱空間中的極小子流形 [J].數(shù)學年刊:A輯,1998,19(6):693-698.(SONG Weidong.On Minimal Submanifolds of a Locally Symmetric Space [J].Chinese Annals of Mathematics:Series A,1998,19(6):693-698.)

[10] 洪濤清,張劍鋒.偽Riemann流形中的2-調(diào)和類空子流形 [J].吉林大學學報:理學版,2009,47(2):257-260.(HONG Taoqing,ZHANG Jianfeng.2-Harmonic Space-Like Submanifolds in Pseudo-Riemann Manifold [J].Journal of Jilin University:Science Edition,2009,47(2):257-260.)

(責任編輯：趙立芹)

MaximumTimelikeSubmanifoldinaLocallySymmetricPseudo-RiemannianManifold

LI Ying,SONG Weidong

(CollegeofMathematicsandComputerScience,AnhuiNormalUniversity,Wuhu241003,AnhuiProvince,China)

Based on the moving frames,an integral inequality about maximal timelike submanifold was obtained in the locally symmetric pseudo-Riemannian manifold and a pinching theorem about the squared norm of the second fundamental form for the compact maximal timelike submanifold was gived in locally symmetric pseudo-Riemannian manifold.

pseudo-Riemannian manifold;locally symmetric;maximum timelike submanifold;totally geodesic timelike submanifold

10.13413/j.cnki.jdxblxb.2015.03.20

2014-09-15.

李 影(1991—),女,漢族,碩士研究生,從事微分幾何的研究,E-mail:909789714@qq.com.通信作者:宋衛(wèi)東(1958—),男,漢族,教授,從事微分幾何的研究,E-mail:swd56@sina.com.

國家自然科學基金(批準號:11071005)和安徽省教育廳自然科學重點項目(批準號:KJ2010A125).

O186.12

：A

：1671-5489(2015)03-0457-04