ZHAO Li-hui,WANG Cai-hong

(1.School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471023, China;Department of Mathematics,Zhejiang University,Hangzhou 310027,China;2.College of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo 454000,China)

Generalized Crossed Products and L-R Smash Products of Multiplier Hopf Algebras

ZHAO Li-hui1,WANG Cai-hong2

(1.School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471023, China;Department of Mathematics,Zhejiang University,Hangzhou 310027,China;2.College of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo 454000,China)

In this paper we generalize the notions of crossed products and L-R smash products in the context of multiplier Hopf algebras.We use comodule algebras to def i ne generalized diagonal crossed products,L-R smash products,two-sided smash products and two-sided crossed products and prove that they are all associative algebras.Then we show the isomorphic relations of them.

multiplier Hopf algebra;diagonal crossed product;L-R smash product;twosided smash product;two-sided crossed product

§1.Introduction

Multiplier Hopf algebras were introduced by A Van Daele in[12]as natural generalizations of Hopf algebras.The motivating example is the dual of an inf i nite dimensional group algebra with the comultiplication def i ned as dual to the product in the group.Dif f erent from a Hopf algebra,the underlying algebra of a multiplier Hopf algebra is no longer assumed to have an identity and the comultiplication is modif i ed.It has been argued in several papers(see[7,13]) why such a generalization is important.

Actions and coactions on algebras are an important part of the theory of Hopf algebras, and they have been extended to multiplier Hopf algebras.Using them one can construct many kinds of non-trivial algebra structures on tensor products.

Diagonal crossed products over quasi-Hopf algebras were f i rst introduced by S Majid in[10] in the form of implicit Tannaka-Krein reconstruction procedure and studied later by F Hausser and F Nill in[9].The notion of L-R smash product was introduced and studied in a series of [1-4],based on the theory of deformation quantization.Applying the coactions of multiplier Hopf algebra,in this paper we def i ne more general versions of diagonal crossed products,LR smash products,two-sided smash products and two-sided crossed products and study their relations.

In the following we recall some def i nitions of multiplier Hopf algebras.

Let A be an algebra with or without identity.We denote by M(A)the multiplier algebra of A.If the product in A is non-degenerate,that is,if ab=0 for all b implies a=0 and ab=0 for all a implies b=0,then there is a natural embedding from A into M(A).And it is easy to see that if A has an identity then the product is automatically non-degenerate and A=M(A).

A comultiplication on A is a homomorphism Δ:A→M(A?A)such that Δ(a)(1?b)and (a?1)Δ(b)are elements of A?A for all a,b∈A and Δ is coassociative in the following sense

for all a,b,c∈A.

A pair(A,Δ)in which A is an algebra with a non-degenerate product and Δ is a comultiplication on A,is called a multiplier Hopf algebra if the linear maps T1,T2:A?A→A?A, def i ned by

are bijective.We say that(A,Δ)is regular if(A,Δ)is again a multiplier Hopf algebra where Δ0is the opposite comultiplication.In a regular multiplier Hopf algebra the antipode is invertible and from A to A instead of the multiplier algebra M(A),see[13].

A vector space R is a left A-module if there is a bilinear map A?R→R de fi ned by a?x■→a·x satisfying(aa0)·x=a·(a0·x)for all a,a0∈A and x∈R.Moreover,if AR=R then the left A-module R is called unital.It is similar to de fi ne a(unital)right A-module. Throughout this paper we work with a multiplier Hopf algebra A and unital modules over a fi xed fi eld k.The Sweedler notation for regular multiplier Hopf algebras is used in several papers such as[7]and[14].So in this paper we will also use it if the comultiplication of a multiplier Hopf algebra is“well-covered”which∑ is a new concept introduced in[7].But here we will write the comultiplication Δ(a)(1b)=a1a2b for a,b∈A.

§2.Generalized Crossed Products and L-R Smash Products

We f i rstly give the def i nitions of a bimodule algebra and a bicomodule algebra.

Def i nition 1Let A be a regular multiplier Hopf algebra.An algebra R is called an A-bimodule algebra,if for all a,b∈A,x,x0∈R the following conditions hold

(1)R is a unital left A-module and unital right A-module such that(a·x)·b=a·(x·b);

(2)a·(xx0)=∑(a1·x)(a2·x0)and(xx0)·a=∑(x·a1)(x0·a2).

Example 1Let A be a multiplier Hopf algebra,E be a left A-module algebra and D be a right A-module algebra.Then E?D is an A-bimodule algebra such that

for all a∈A,e∈E and d∈D.

Before we def i ne a bicomodule algebra of a multiplier Hopf algebra,we need to recall the def i nition of a coaction in multiplier Hopf algebras[15].

Def i nition 2Let A be a multiplier Hopf algebra,and R an algebra with a non-degenerate product.An injective homomorphism Γ:R→M(A?R)is a left coaction of A on R if the following conditions hold

(i)Γ(R)(A?1)?A?R,(A?1)Γ(R)?A?R; (ii)(idA?Γ)Γ=(ΔA?idR)Γ.

At the same time,R is called a left A-comodule algebra.

Note 1(1)For any a∈A,x∈R,there exists an element e∈A such that ea=a and Γ(x)(a?1)=Γ(x)(e?1)(a?1).By the formula Γ(x)(e?1)∈A?R,we can write Γ(x)(e?1)=∑x?1?x0and

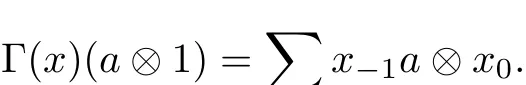
Similarly,(a?1)Γ(x)=∑ax?1?x0.

(2)The right hand side of condition(ii)makes sense,because ΔAis non-degenerate.Def i ning

for all x,y∈R,a,b∈A,we have(idA?Γ)Γ(x)∈M(A?A?R).

(3)The notations of a right coaction of A on R and a right A-comodule algebra can be def i ned which is denoted byˉΓ:R→M(R?A),ˉΓ(x)=∑x(0)?x(1).

Def i nition 3Let A be a multiplier Hopf algebra and R an algebra.Assume that R is a left A-comodule algebra and also a right A-comodule algebra.Then R is an A-bicomodule algebra if

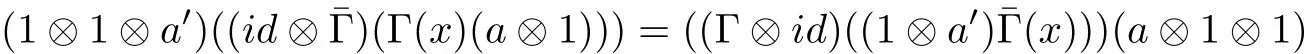
for all x∈R,a,a0∈A.

Example 2Let(A,Δ)be a multiplier Hopf algebra,Q be a left A-comodule algebra and P be a right A-comodule algebra.Then Q?P is an A-bicomodule algebra.

ProofIf ΓQis the left coaction of Q andˉΓPis the right coaction of Q,we can construct the maps ΓQ?P:Q?P→M(A?(Q?P))andˉΓQ?P:Q?P→M((Q?P)?A)such that

for all a∈A,q,q0∈Q and p,p0∈P.Therefore it is easy to see that

and

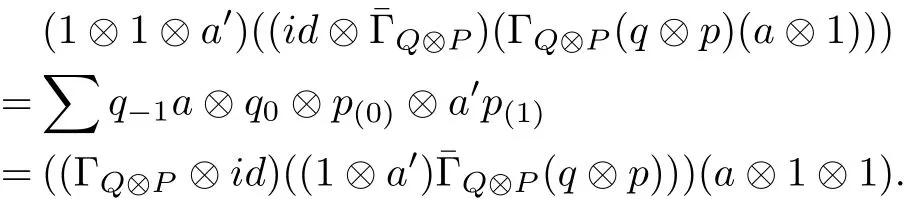
By the def i nition of a bicomodule algebra we prove the result.

Using bimodule algebras and bicomodule algebras,we will show the def i nitions of generalized crossed products and L-R smash products in multiplier Hopf algebras.

?Generalized Diagonal Crossed Product

Let(A,Δ)be a regular multiplier Hopf algebra,B be an A-bimodule algebra and C be an A-bicomodule algebra.We def i ne

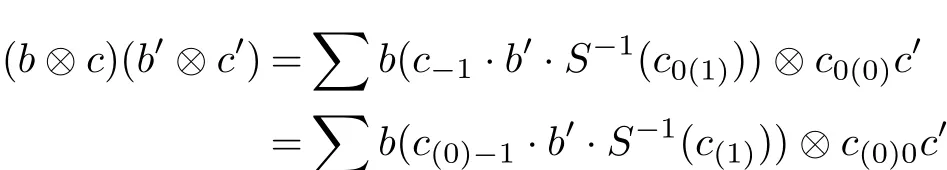
for all b,b0∈B and c,c0∈C.

Note 2The above formula is well-def i ned since left and right modules of B are unital.

Def i nition 4Let(A,Δ)be a regular multiplier Hopf algebra,B be an A-bimodule algebra and C be an A-bicomodule algebra.Then B?C with above multiplication is called a generalized diagonal crossed product which is denoted by B??C.Moreover,B??C is called a diagonal crossed product if C=A and the coactions are given by Δ.

?Generalized L-R Smash Product

Let(A,Δ)be a multiplier Hopf algebra,B be an A-bimodule algebra and C be an A-bicomodule algebra.For any b,b0∈B and c,c0∈C we give the multiplication on B?C as

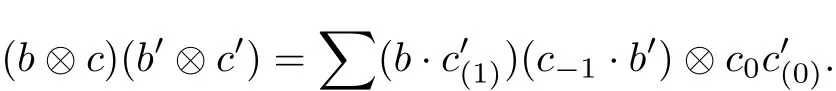
Note 3(1)The above formula is well-def i ned since left and right modules of B are unital. (2)If(A,Δ)be a regular multiplier Hopf algebra and C=A in which the coactions are given by Δ,the above structure is exactly an ordinary L-R smash product of B?A.

Def i nition 5Let(A,Δ)be a multiplier Hopf algebra,B be an A-bimodule algebra and C be an A-bicomodule algebra.Then B?C with above multiplication is called a generalized L-R smash product which is denoted by.If both B and C have an identity,then 1is an identity of.A generalized L-R smash product becomes a generalized smash product which is denoted byif the right A-module B or the right A-comodule C is trivial.

?Two-sided Generalized Smash Product

Let(A,Δ)be a multiplier Hopf algebra.Suppose that E is a left A-module algebra,D is a right A-module algebra and C is an A-bicomodule algebra.For any e,e0∈E,d,d0∈D and c,c0∈C we def i ne a multiplication on ECD giving by

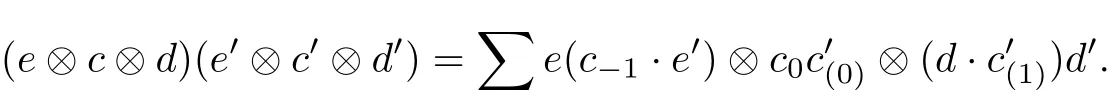
Proposition 1The above multiplication on E?C?D is associative.

ProofBy direct calculations we obtain

for all e,e0∈E,d,d0∈D and c,c0∈C.

Def i nition 6Let(A,Δ)be a multiplier Hopf algebra.Suppose that E is a left A-module algebra,D is a right A-module algebra and C is an A-bicomodule algebra.Then E?C?Dwith the above multiplication is called a two-sided generalized smash product,which is denoted by ECD.Moreover,ECD is called a two-sided smash product if A is a regular multiplier Hopf algebra and C=A.If E,C and D all have an identity,1E1C1Dis an identity of ECD.

?Generalized Two-sided Crossed Product

Let(A,Δ)be a multiplier Hopf algebra.Suppose that B is an A-bimodule algebra,P is a right A-comodule algebra and Q is a left A-comodule algebra.We def i ne a multiplication on PBQ giving by

where p,p0∈P,q,q0∈Q and b,b0∈B.

Proposition 2The above multiplication on P?B?Q is associative.

ProofUsing the def i nition we obtain

for all p,p0,p00∈P,q,q0,q00∈Q and b,b0,b00∈B.

Def i nition 7Let(A,Δ)be a multiplier Hopf algebra.Suppose that B is an A-bimodule algebra,P is a right A-comodule algebra and Q is a left A-comodule algebra.Then P?B?Q with the above multiplication is called a generalized two-sided crossed product,which is denoted by P■B■Q.Similarly,1P■1B■1Qis an identity of P■B■Q if P,Q and B all have an identity.

§3.Isomorphisms

In this section we will consider the isomorphic relations between the generalized crossed products and L-R smash products which we def i ned in Section 2.

Proposition 3Let(A,Δ)be a regular multiplier Hopf algebra.

(1)If E is a left A-module algebra,D is a right A-module algebra and C is an A-bicomodule algebra,then??C～=as algebras.

(2)If B is an A-bimodule algebra,P is a right A-comodule algebra and Q is a left A-comodule algebra,then B(QP)～=PBQ as algebras.

ProofWe def i ne the linear maps

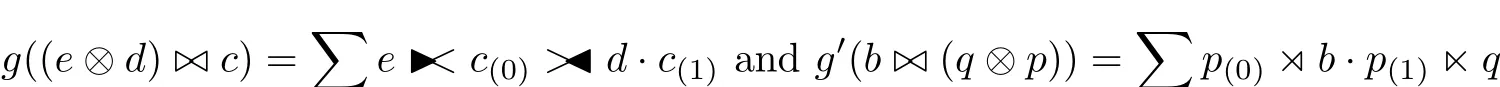
for all e∈E,d∈D,c∈C and b∈B,q∈Q,p∈P.By the def i nitions of g and g0and the multiplications of crossed products we get

for all e,e0∈E,d,d0∈D and c,c0∈C and

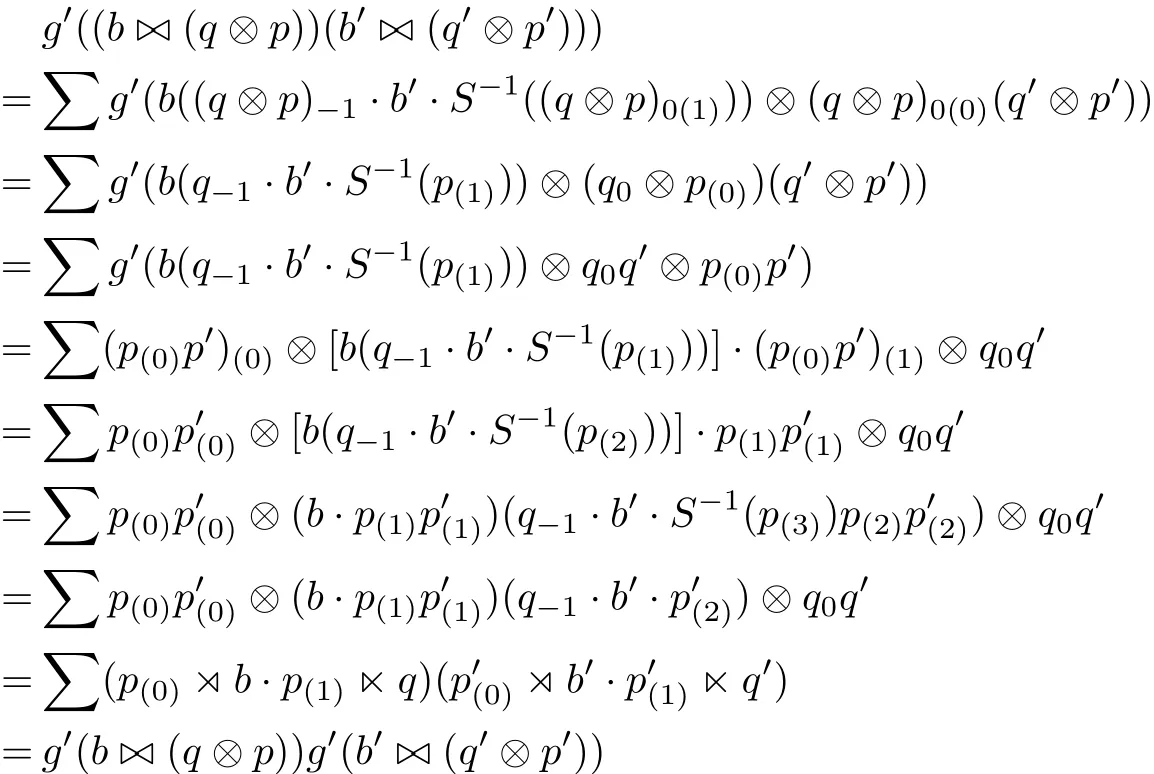
for all b,b0∈B,q,q0∈Q and p,p0∈P.Furthermore,remark that the antipode of A is invertible since A is regular.Hence g and g0are invertible and the inverse maps are given respectively by

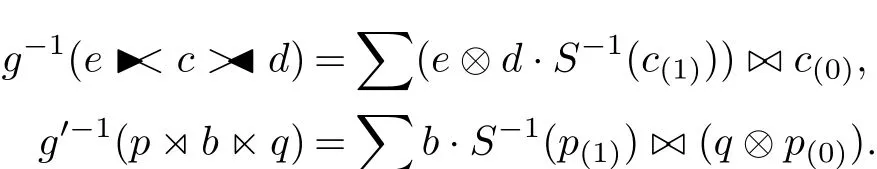
So g and g0are algebra isomorphisms.

Proposition 4Let(A,Δ)be a multiplier Hopf algebra.

(1)If E is a left A-module algebra,D is a right A-module algebra and C is an A-bicomodule

(2)If B is an A-bimodule algebra,P is a right A-comodule algebra and Q is a left A-

ProofBy Example 1 and Example 2,E?D is an A-bimodule algebra and Q?P is

where e∈E,d∈D,c∈C and b∈B,q∈Q,p∈P.It is clear that f and f0are bijective. Using the multiplications of generalized L-R smash products and two-sided crossed products respectively,we have

for all e,e0∈E,d,d0∈D and c,c0∈C and

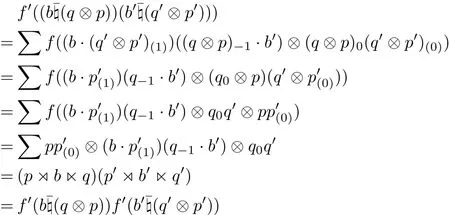
for all b,b0∈B,q,q0∈Q and p,p0∈P.Therefore f and f0are algebra isomorphisms.

By Proposition 3 and Proposition 4 we obtain the following properties.

Corollary 2Let(A,Δ)be a regular multiplier Hopf algebra.

(1)If E is a left A-module algebra,D is a right A-module algebra and C is an A-bicomodule

(2)If B is an A-bimodule algebra,P is a right A-comodule algebra and Q is a left A-comodule algebra,then Bˉ■(Q?P)～=B??(Q?P)as algebras.

Corollary 3Let(A,Δ)be a regular multiplier Hopf algebra.Suppose that E is a left A-module algebra,D is a right A-module algebra,P is a right A-comodule algebra and Q is a left A-comodule algebra.Then

[1]BIELIAVSKY P,BONNEAU P,MAEDA Y.Universal deformation formulae,symplectic Lie groups and symmetric spaces[J].2003,Math QA/0308189.

[2]BIELIAVSKY P,BONNEAU P,MAEDA Y.Universal deformation formulae for three-dimensional solvable Lie groups[J].2003,Math QA/0308188.

[3]BONNEAU P,GERSTENHABER M,GEAQUINTO A,et al.Quantum groups and deformation quantization:explicit approaches and implicit aspects[J].J Math Phys,2004,45:3703-3741.

[4]BONNEAU P,STERNHEIMER D.Topological Hopf Algebras,Quantum Qroups and Deformation Quantization,in“Hopf Algebras in Noncommutative Geometry and Physics”,Lecture Notes in Pure and Appl Math[C].New York:Marcel Dekker,2005,239:55-70.

[5]DELVAUX L.Semi-direct products of multiplier Hopf algebras:smash products[J].Comm Alg,2002,30(12): 5961-5977.

[6]DELVAUX L.Twisted tensor product of multiplier Hopf(*-)algebras[J].J Alg,2003,269:285-316.

[7]DRABANT B,VAN D A,ZHANG Yin-huo.Actions of multiplier hopf algebras[J].Comm Alg,1999,27(9): 4117-4127.

[8]DRABANT B,VAN DAELE A.Pairing and quantum double of multiplier Hopf algebras[J].Algebras and Representation Theory,2001,4:109-132.

[9]HAUSS F,NILL F.Diagonal crossed products by duals of quasi-quantum groups[J].Rev Math Phys,1999, 11:553-629.

[10]MAJID S.Quantum double for quasi-Hopf algebras[J].Lett Math Phys,1998,45:1-9.

[11]PANAITE F,OYSTAEYEN F V.L-R-smash product for(quasi)Hopf algebras[J].J Alg,2007,309(1): 168-191.

[12]VAN DAELE A.Multiplier Hopf algebras[J].Transactions of the American Mathematical Society,1994, 342(2):323-366.

[13]VAN D A.An algebraic framework for group duality[J].Advances in Mahtematics,1998,140:323-366.

[14]VAN D A,WANG Shuang-hong.The Larson-Sweeldler theorem for multiplier Hopf algebras[J].J Alg,2006, 296:75-95.

[15]VAN D A,ZHANG Yin-huo.Calois theory for multiplier Hopf algebras with integrals[J].Algebras and Representation Theory,1999,2:83-106.

[16]ZHAO Li-hui,LU Di-ming,FANG Xiao-li.L-R smash products of multiplier Hopf algebras[J].Appl Math, 2008,23B(1):83-90.

tion:16W30,16S40

CLC number:O151.21Document code:A

1002–0462(2014)02–0283–09

date:2012-12-19

Supported by the Scientif i c Research Foundation for Doctoral Scientists of Henan University of Science and Technology(09001303);Supported by the National Natural Science Foundation of China(11101128)

Biographies:ZHAO Li-hui(1979-),female,native of Luoyang,Henan,a lecturer of Henan University of Science and Technology,Ph.D.,engages in noncommutative algebra;WANG Cai-hong(1980-),female,native of Zhengzhou,Henan,a lecturer of Henan Polytechnic University,Ph.D.,engages in noncommutative algebra.