HAN Guo-qiang,YAO Hai-lou

(College of Applied Sciences,Beijing University of Technology,Beijing 100124,China)

Biserial Incidence Algebras

HAN Guo-qiang,YAO Hai-lou

(College of Applied Sciences,Beijing University of Technology,Beijing 100124,China)

Let K be an algebraically closed f i eld and A be a f i nite dimensional algebra over K.In this paper we give a classif i cation of biserial incidence algebras with quiver methods.

biserial algebras;incidence algebras;representation type;quivers

§1.Introduction

In this paper,we denote by K a fi xed algebraically closed fi eld and by A a fi nite dimensional associative algebra over K.Let Q be a fi nite quiver,and write Q0and Q1for the sets of vertices and arrows respectively.If α is an arrow we write s(α)for its starting vertex and t(α)for its end vertex.A path of length s≥1 is an ordered sequence of arrows α1α2···αs, with t(αi)=s(αi+1)for 1≤i＜s.A subquiver of a quiver Q=(Q0,Q1,s,t)is a quiver=,s0,t0)such that?Q1and the restrictions sof s,t toare respectively equal to s0,t0(that is,if α:a→b is an arrow in Q1such that α∈and a,b∈,then s0(α)=a and t0(α)=b).Such a subquiver is called full ifequals the set of all those arrows in Q1whose starting vertex and end vertex both belong to,that is,={α∈Q1|s(α)∈and t(α)∈}.A full subquiver Q0of a quiver Q is de fi ned to be convex in Q if,for any path x0→x1→···→xtin Q with x0,xt∈,we have xi∈for all i such that 0≤i≤t.For a fi xed algebra A,let QAbe its quiver.By Gabriel Theorem,we have A～=KQA/IA,where IAia an admissible ideal of path algebra KQA.

Uniserial algebras and serial algebras have been described in detail in[1-2].As a natural generalization of serial algebras,the notions of biserial algebras were introduced.By de fi nition an algebra is biserial if each fi nite dimensional indecomposable projective left and right module P contains two uniserial submodules whose sum is the unique maximal submodule(i.e.,theradical)of P and whose intersection is either zero or simple(a module is uniserial if it has a unique composition series).The condition fi rst appeared in the work of Tachikawa[3]and it was formalized by Fuller[4].Examples include blocks of group algebras with cyclic defect groups; fi nite dimensional quotients of the algebras in Ringel’s list of tame local algebras[5],the special biserial algebras[67]and the regular biserial algebras[8].The structure and representation type of biserial algebras was researched in[9-10].

Incidence algebras are de fi ned over a fi nite poset,and given by a quiver with relations.Let (Σ,≤)be a fi nite poset.The quiver of A(Σ)has as vertices the elements of Σ.For x,y∈Σ, there is exactly one arrow from x to y if and only if y＜x and there is no element z∈Σ such that y＜z＜x.In other words,QAis the Hasse diagram of the poset Σ.For two paths γ and μin QA,we say that γ andμare parallel if they have the same starting vertex and the same end vertex.The ideal IAof KQAis generated by all di ff erences γ?μ,with γ,μparallel paths. We say that A=KQA/IAis an incidence algebra.In this paper,we use quiver methods to give a classi fi cation of connected biserial incidence algebras.

§2.The Main Result and Its Proof

From the def i nition of biserial algebras one can easily obtain the following property.

Property 1Let A～=KQA/IAbe a biserial algebra,then the numbers of arrows starting, respectively ending,at any f i xed vertex of QAis bounded by 2.In this case we say that QAis a biserial quiver.

Lemma 1Let A～=KQA/IAbe a biserial incidence algebra,then there is no subquiver in the form of Figure 1 in QA.

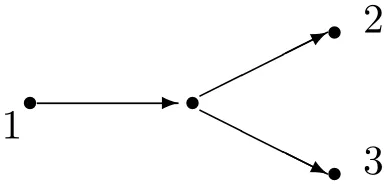
Figure 1D4 Quiver

ProofSuppose that Figure 1 is a full convex subquiver of QA.The right A-module radP(1)(see Figure 1)cannot be written as a sum of two uniserial modules whose intersection is simple or zero.A contradiction!

Suppose that Figure 1 is a subquiver of QA,but not a full convex subquiver of QA.By Property 1,the full convex subquiver of QAgenerated by Figure 1 is a subquiver in which there is at most one path from vertex 1 to vertex 2 or one path from vertex 1 to vertex 3.In any case,the right A-module radP(1)cannot be written as a sum of two uniserial modules whose intersection is simple or zero.A contradiction!

Lemma 2Let A～=KQA/IAbe a biserial algebra,then the underlying graph of QAis of Anor?An.

ProofAssume that the underlying graph of QAis of An.Then A is a biserial incidence algebra.

Assume that the underlying graph of QAis not of An.Then there is no subquiver in the form of Figure 1 in QAby Lemma 1.By the de fi nition of biserial algebra,there is no subquiver in the form of Figure 1 inHence the underlying graph of QAis ofA?nby Property 1.If IA=0,then QAis a quiver in the form of Figure 2.If IA/=0,then QAis a quiver in the form of Figure 3.

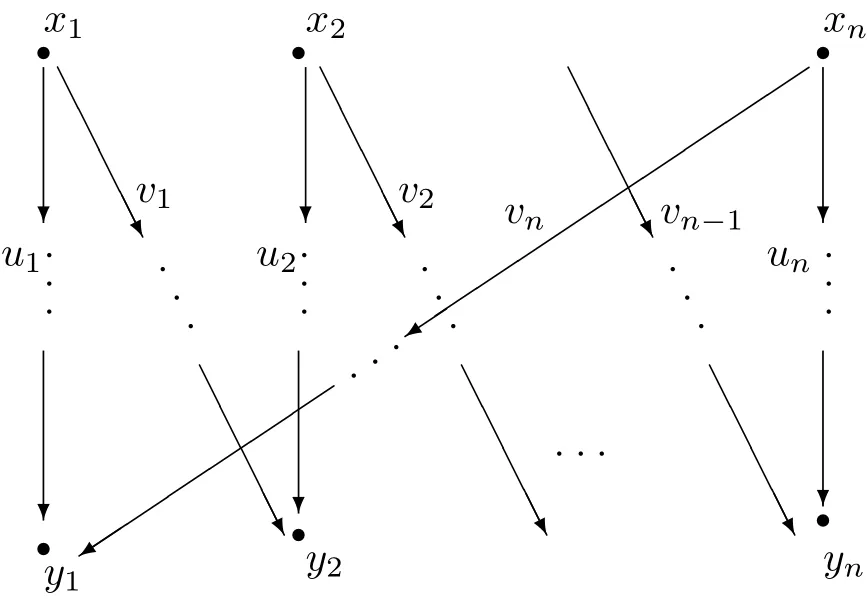
Figure 2Crown Quiver

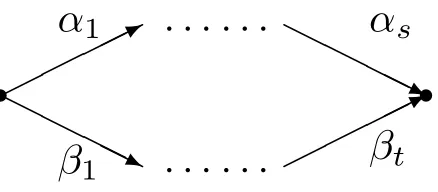
Figure 3Quiver with Relations

TheoremLet A～=KQA/IAbe a biserial incidence algebra,then QAis Anor a quiver in the form of Figure 2 and Figure 3.

ProofThe conclusion is easily obtained by Lemma 2.

AcknowledgementWe would like to thank professor Lin Yanan for his help and suggestions when we prepare this version of the article.

[1]DROZD YU A,KIRICHENKO V V.Finite Dimensional Algebras[M].Berlin,Heidelberg,New York: Springer-Verlag,1994.

[2]AUSLANDER M,REITEN I,SMALO S O.Representation Theory of Artin Algebras[M].Cambridge: Cambridge University Press,1995.

[3]TACHIKAWA H.On algebras of which every indecomposable representation has an irreducible one as the top or the bottom Loewy constituent[J].Math Z,1961,75:215-227.

[4]FULLER K R.Biserial Rings,in:Lecture Notes in Mathematics 734[C].Berlin:Springer,1979,64-90.

[5]RINGEL C M.The Representation Type of Local Algebras,in:Lecture Notes in Mathematics 488[C]. Berlin:Springer,1975,282-305.

[6]SKOWRO′NSKI A,WASCHB¨USCH J.Representation-f i nite biserial algebras[J].J Reine Angew Math,1983, 345:172-181.

[7]WALD B,WASCHB¨USCH J.Tame biserial algebras[J].J Algebras,1985,95(2):480-500.

[8]POGORZALY Z.Regularly biserial algebras,in:Banach Center Publications 26,Part I[C].Warsaw:PWN, 1990,371-384.

[9]VILA-FREYER R,CRAWLEY-BOEVEY W.The structure of biserial algebras[J].J London Math Soc, 1998,57(1):41-54.

[10]CRAWLEY-BOEVEY W.Tameness of biserial algebras[J].Arch Math(Basel),1995,65(5):399-407.

tion:16G20,16G60

CLC number:O153.3Document code:A

1002–0462(2014)02–0244–03

date:2012-09-18

Supported by the National Natural Science Foundation of China(11271119);Supported by the Natural Science Foundation of Beijing(1122002)

Biography:HAN Guo-qiang(1975-),male,native of Qixian,Shanxi,a Ph.D.student of Beijing University of Technology,engages in representation theory of algebra.