FENG Yan-qing,WANG Zhong-ying

(Department of Mathematics,Changzhou Institute of Technology,Changzhou 213000,China)

The Existence and Uniqueness of the Solution for Periodical Boundary Value Problems of 2kth Order Dif f erential Equations with Resonance

FENG Yan-qing,WANG Zhong-ying

(Department of Mathematics,Changzhou Institute of Technology,Changzhou 213000,China)

In this paper,a new set of sufficient conditions related to an initial value problem and global homeomorphism is obtained in discussing the existence and uniqueness of 2πperiodic solution for 2kth order dif f erential equations with resonance.The key role is played by nonnegative auxiliary scalar coercive function.The result of this paper generalizes some existed theorems.

initial value problem;global homeomorphism;periodic solution;nonnegative auxiliary scalar coercive function;resonance

§1.Introduction

Consider the system of the 2kth order dif f erential equations

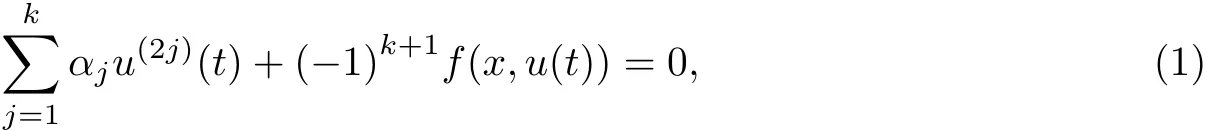
where u∈Rn,αjare constants.The set=0,1,···}is called the set of points of resonance and the equation(1)is said to be the resonance.Equation (1)is called the nonresonance if the following conditions hold(see[5]).

(H1)f∈C1(R×Rn),f(t+2π,x)=f(t,x)and the Jacobian matrix fx=fixjis a symmetric n×n matrix.

(H2)There exist two constant symmetric n×n matrices A and B such that

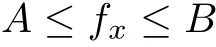
and if λ1≤λ2≤···≤λnandμ1≤μ2≤···≤μnare the eigenvalues of A and B,respectively, then

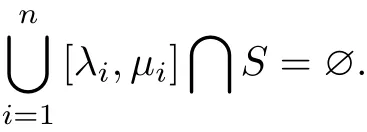
Several authors had discussed the existence and uniquence of 2π periodic solution of this problem,such as[1-3].In this paper,we give a new set of sufficient condition for the problem under a resonant case by using an initial value problem and global homeomorphism.To our knowledge,there is few of the application of initial value problem and global homeomorphism to this problem.Additionally,the result of this paper generalize some existed theorem and make them as corollary.

§2.Preliminaries

In this paper the basic element is a C1mapping f:D?X→Y,with X,Y being Banach space,D?X is open and connected and with derivative everywhere invertible

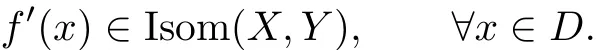
Consequently f is a local dif f eomorphism at every point by the inverse function theorem. However,an important problem in nonlimear analysis is to f i nd appropriate condition under which a local difeomorphism becomes a global one.Therefore we f i rst give sufficient conditions for f to be a global homeomorphism of D onto Y,which it is to be used to prove our main theorem.

Def i nition 2.1[4]The continuous mapping f:D?X→Y satisf i es condition(C)if and only if for any continuous function p:[0,a)→D?X,a∈(0,1]such that f(p(t))= q(t),t∈[0,a],where q(t)=(1?t)y1+ty2is any line in Y,there is a sequence{tn}such that

Theorem 2.2[4]Let f:D?X→Y be a local homeomorphism,then f is a global homeomorphism of D onto Y if and only if f satisf i es condition(C).

Secondly,the following Comparison theorem[4]plays an important role in proving the sufficient condition for the existence of a unique 2π-periodic solution of the problem(1).

Let E be an open(t,x)-set in R2and g∈C[E,R].Consider the scalar dif f erential equation with an initial condition

Assume that there exists a sequence{tk}such that t0≤tk→a as k→∞and u0=exists.If g(t,u)is bounded on the intersection of E and a neighbourhood of(a,u0), then.If,in addition,g(a,u0)is de fi ned such that g(t,u)is continuous at(a,u0), then u(t)is continuously di ff erentiable on[t0,a]and is a solution of(2)on[t0,a](see[5]).In this case the solution u(t)can be extended as a solution to the boundary of E.

Theorem 2.3(Comparison Theorem[5])Let E be an open(t,u)-set in R2and g∈C[E,R].Suppose that[t0,t0+a)is the largest interval in which the maximal solution r(t)of (2)exists.Let m∈C[[t0,t0+a],R],(t,m(t))∈E for t∈[t0,t0+a),m(t0)≤u0and for a fi xed Dini derivative

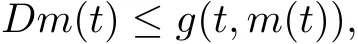
then

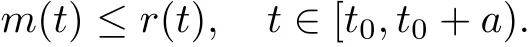
Finally,we shall use nonnegative auxiliary scalar coercive function,that is a continuous mapping k:X→R+with k(x)→+∞as‖x‖→+∞.Furthermore,we also need the directional right derivatives,i.e.,for any x,v∈X,we assume the existence of

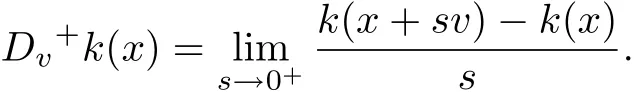
§3.Main Theorem

Consider the boundary value problem

Suppose that the linear operator L:D(L)→X is def i ned bycontinuously Frechet dif f erentiable operator N:D(L)?X→X is def i ned by

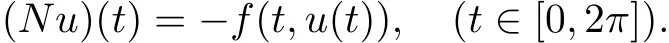
So(3)is equivalent to the operator equation

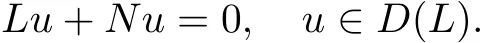
It is convenient to choose X to be a space such that L is densely de fi ned.For this purpose,(2k)[0,2π],for i=1,2,···,n and j=0,1,···,2k?1}.Then L is a linear closed self-adjoint operator with domain D(L)being dense in X and D(L)is a Banach space with respect to the norm

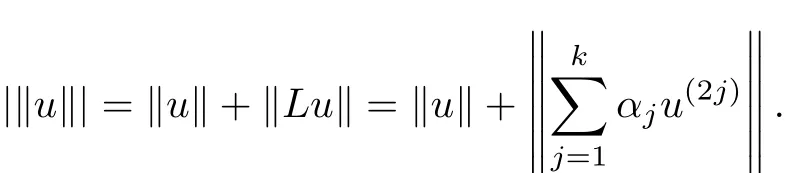
Since this norm is equivalent to the Sobolev normthe Sobolev embedding theorem,D(L)has a compact embedding into[0,2π],wherehas a continuous(2k?1)th derivative on[0,2π]}.

Let Q(u(t))=(fiuj(t,u(t))),i,j=1,···,n,so

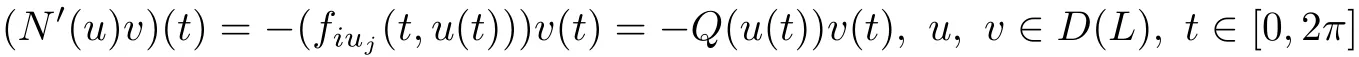
and L+N′(u)=L?Q(u),where Q(u)is a symmetric matrix.Let γ1(u)≤···≤γn(u)be eigenvalues of Q(u)where each eigenvalue is counted according to its multiplicity.Suppose that there exist

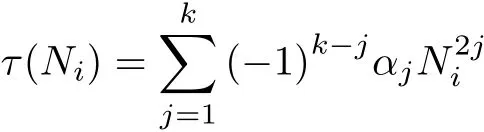
and

such that

where Ni(i=1,···,n)are nonnegative integers.Consider the eigenvalue problem

where u0∈D(L)is f i xed.Since the spectrum of L consists only of the eigenvalues τ(N),it follows that λ is an eigenvalue of(5)if and only if λ=τ(N)?γi(u0)for some 1≤i≤n and some integers τ(N)≥0(see[1]).

By(4),zero is not an eigenvalue of(5),so L?Q(u0)is invertible.Moreover,by the spectral theorem(see[1]),

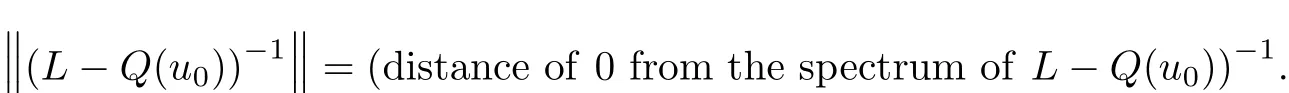
And hence,in this case,

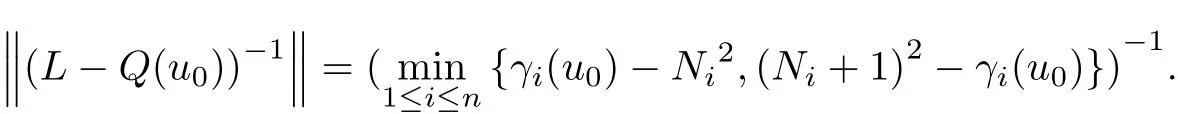
For a given g∈X,let Lu+Nu=g.We have the following theorem.

Theorem 3.1Assume that(i)the condition(H1)holds,(ii)for all u∈D(L),τ(Ni)＜γi(u)＜τ(Ni+1),i=1,···,n,(iii)there exists a coercive function k:X→R+which admits the directional right derivatives DV+k(x)for arbitrary x,x0∈D(L),y∈X,v= g′(x)?1(y?f(x0))and a continuous mapping h:R+→R+such that DV+k(x)≤h(k(x))and for any r0＞0,the maximum solution of the initial value problemis de fi ned on[0,a)and there exists a sequence{tn}such that tn→a,n→∞,=r?is fi nite.Then for each g∈X,there exists a unique solution u satisfying(3)andis absolutely continuous on[0,2π].

ProofBy the above discussion,for all u∈D(L),the operator L+N′(u)is invertible on X.Hence g is a local homeomorphism of D and for?r∈R,

Then,in view of Theorem 2.2,we need only show that g has the property(C).Suppose that there exists continuous function p:[0,a)→D?X such that

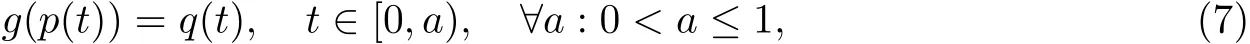
where q(t)=(1?t)y+tf(x0),y∈X,x0∈D.

We need to prove that there exists a real sequence{tn}such that tn→a,n→∞,=r?and(tn)=p?exists and is in D(L).

It is clear that p is di ff erentiable in this case.We have from(7)that

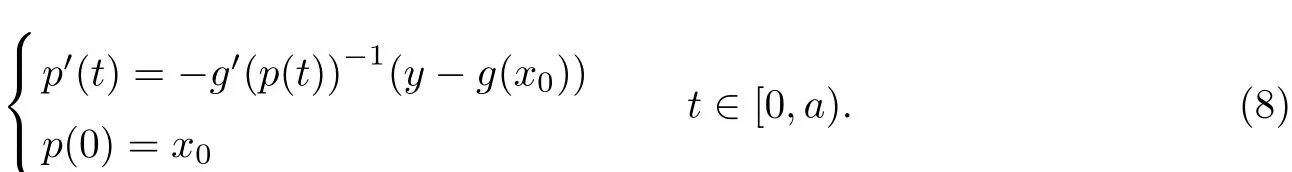
Let v=g′(p(t))?1(y?g(x0)).By the assumption(iii),we have DV+k(x)≤h(k(x))and the maximum solution r(t)of(6)is de fi ned on[0,a)and there exists a sequence tn→a as n→∞such thatr(tn)=r?is fi nite.It follows that r(t)is continuous on[0,a]and there is a constant M1such that|r(t)|≤M1,t∈[0,a].By the comparison theorem[4],we have

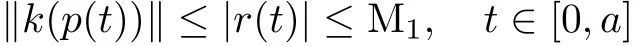
as well as‖p(t)‖≤M2,t∈[0,a)for some constant M2,since k is coercive.Let

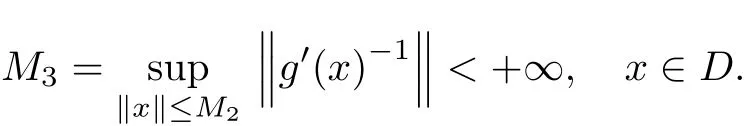
For t1,t2∈[0,a),we have

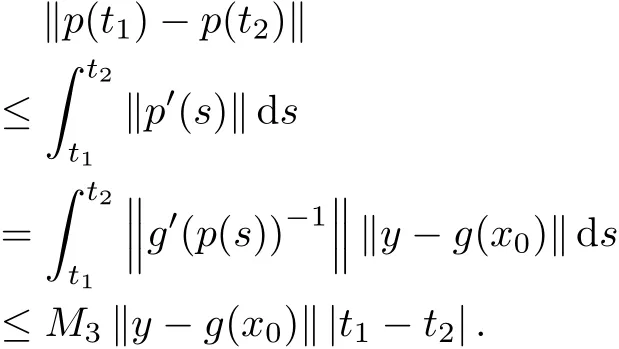
So{p(tn)}is a Cauchy sequence and consequently for the real sequence tn→a as n→∞, thep(tn)=p?exists and g(p?)=y∈X.This proves that p?∈D and g satis fi es the condition(C).The theorem is proved.

Based on the Theorem 3.1,we f i nd that Le in[1],Zhu and Shen[3]results become the special case of the theorem.

Corollary 3.1[1]Suppose that(H1),(H2),there exist two constant symmetric n×n matrices A and B such that A+α(‖u‖)≤fx≤B?β(‖u‖)on R×Rnand the eigenvalues of A and B are

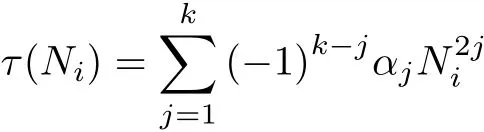
and

respectively,where Ni(i=1,···,n)are nonnegative integers,α(s)andβ(s)are continuous function de fi ned on[0,∞)and(0,∞)andmin(α(s),β(s))ds=∞.Then equation(3)has a unique 2π-periodic solution.

ProofWe need only prove condition(iii)of Theorem 3.1 satis fi ed.De fi ned

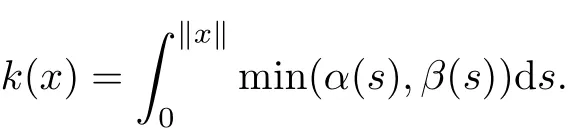
By the condition,we have k(x)→+∞as‖x‖→+∞and

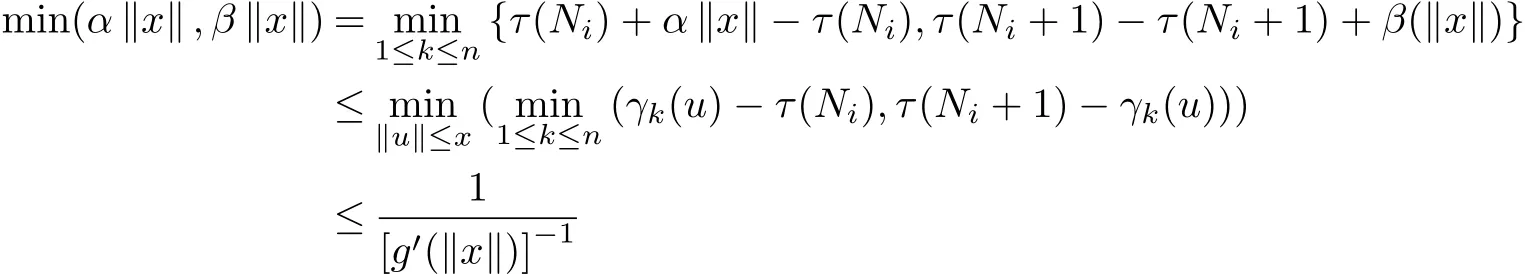
for arbitrary x,x0∈D,y∈X,v=g′(x)?1(y?g(x0))v=g′(x)?1(y?g(x0)),

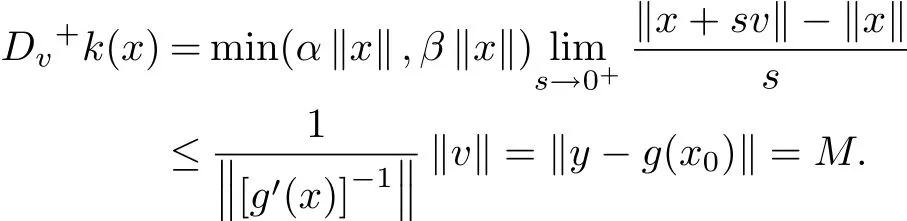
So the corollary is proved.Let δ:R+→R+?{0}be def i ned by

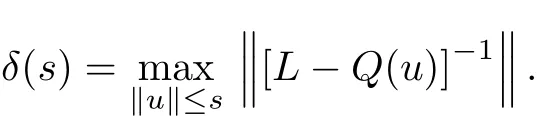
Corollary 3.3[3]Assume that the condition(H1)holds and the eigenvalues of Q(u) satisfy(4).Suppose also that,for arbitrary η∈R the maximum solution y of the initial value problem

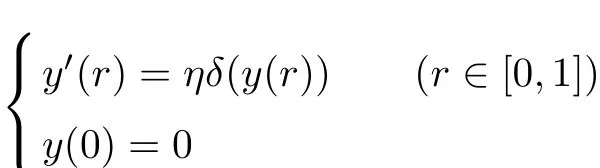
is de fi ned on[0,1]and y(a)=y(s)is fi nite for a∈(0,1].Then,for each f∈X,there exists a unique 2π-periodic solution to the system(3).

ProofBy the condition

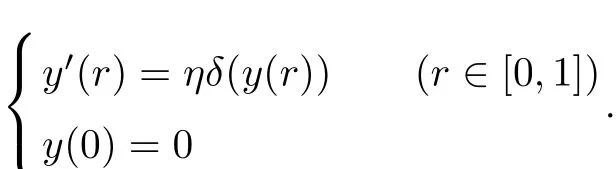
So

[1]LE Wei-guo.Periodic solution for 2kth order ordinary dif f erential equation with resonance[J].J of Math Anal and Appl,2001,259(1):157-167.

[2]CONG F Z.Periodic solution of th order ordinary dif f erential equation with non-resonance[J].Nonlinear Anal,1998,32(6):787-793.

[3]ZHU Jan,SHEN Zu-he.On the existence of periodic solutions of 2kth order dif f erential equations with resonance[J].Journal of Nanjing University Mathematical Biquarterly,2003,20(2):7-15.

[4]PLASTOCK R.Homeomorphism between Banach space[J].Trans Am Math Soc,1974,200(1):169-183.

[5]LAKSHMIKANTHAM V,LEEDA S.Dif f erential and Integral Inequalities Vol.II[M].New York:Academic Press,1969.

[6]SHEN Zu-he.On the periodic solution to the Newtonian equation of motion[J].Nonlinear Analysis,1989, 13(2):145-149.

[7]SHEN Zu-he,WOLFE M A.On the existence of periodic solution of periodically perturbed conservative systems[J].Mathematical Analysis and Applications,1990,153(1):78-83.

[8]FENG Yan-qing,WANG Zhong-ying.A resonance condition in the periodic boundary for 2kth order dif f erential equations[J].Journal of Anhui University,2011,35(1):10-15.

[9]FENG Yan-qing,WANG Zhong-ying,ZHANG Dan-qing.Global homeomorphism and the existence of solutions for periodically perturbed conservative systems[J].Journal of Nanjing University Mathematical Biquarterly,2011,28(1):24-32.

tion:34B15

CLC number:O175.8Document code:A

1002–0462(2014)02–0203–07

date:2012-06-18

Supported by the Natural Science Foundation of Changzhou Instituty of Technology(YN09090);Supported by the Natural Science Foundation of Jiangsu Province(13KJD110001)

Biographies:FENG Yan-qing(1969-),female,native of Yiwu,Zhejiang,an associate professor of Changzhou Institute of Technology,M.S.D.,engages in nonlinear function analysis and application;WANG Zhongying(1968-),female,native of Changzhou,Jiangsu,an associate professor of Changzhou Institute of Technology, M.S.D.,engages in nonlinear function analysis.