WEI Han-yu,XIA Tie-cheng

(1.College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China;2.Department of Mathematics,Shanghai University,Shanghai 200444,China)

A New Nonlinear Integrable Couplings of Yang Equations Hierarchy and Its Hamiltonian Structure

WEI Han-yu1,2,XIA Tie-cheng2

(1.College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China;2.Department of Mathematics,Shanghai University,Shanghai 200444,China)

Based on a kind of non-semisimple Lie algebras,we establish a way to construct nonlinear continuous integrable couplings.Variational identities over the associated loop algebras are used to furnish Hamiltonian structures of the resulting continuous couplings. As an illustrative example of the scheme is given nonlinear continuous integrable couplings of the Yang hierarchy.

zero curvature equations;integrable couplings;variational identities

§1.Introduction

Integrable couplings[12]are coupled systems of integrable equations,which has been introduced when we study of Virasoro symmetric algebras.It is an important problems to look for integrable couplings because integrable couplings have much richer mathematical structures and physical meanings.In recent years,many methods of searching for integrable couplingshave been developed[39],for example,the spectral matrices as follows

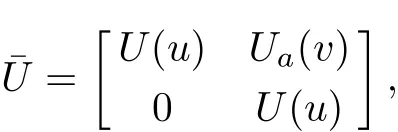
where the sub-spectral matrix U is associated with the given integrable equation ut=K(u). However,researcher f i nd out that obtained integrable couplings is relative simple.So in order to get better integrable couplings of the known integrable system,we need to introduce an enlarged relatively complex spectral matrix[10-11]

From a zero curvature representation

where

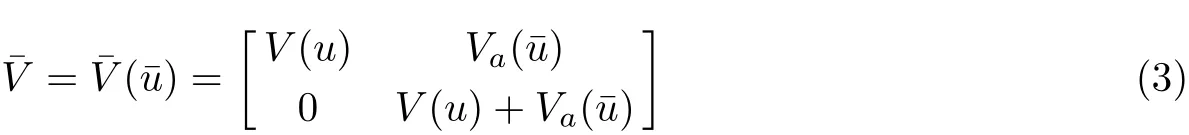
andˉu consist of u and v,we can obtain

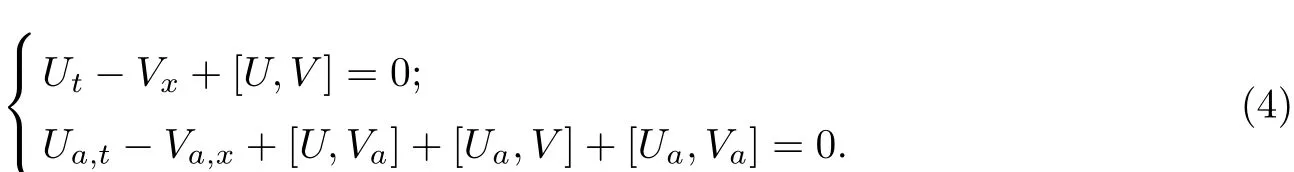
This is an integrable couplings of Eq(1),and it is a nonlinear integrable coupling because the commutator[Ua,Va]can generate nonlinear terms.

Let us take a solutionˉW to the enlarged stationary zero curvature equation

Then,we use the variational identity[6-7]

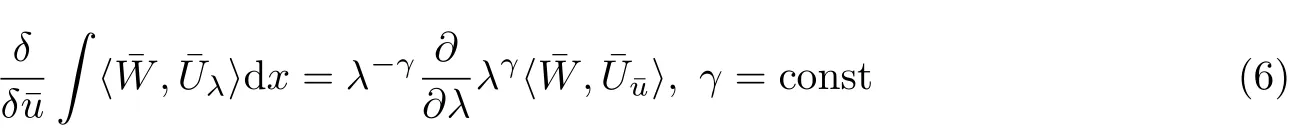
to search for the Hamiltonian structures of the integrable couplings[7].In the variational identity(6),〈.,.〉is non-degenerate,symmetric and ad-invariant bilinear form over the Lie algebra

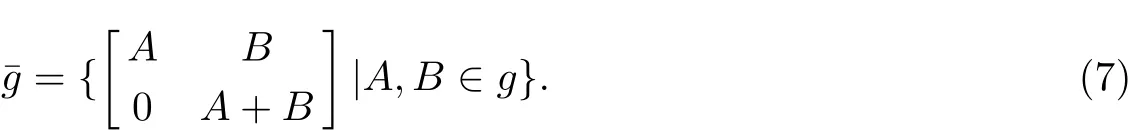
In what follows,we will make an application of this general scheme to the Yang hierarchy.

§2.The Integrable Couplings of the Yang Equations Hierarchy

2.1Yang Hierarchy

From the spectral problem[12]

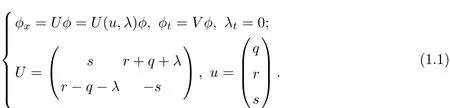
Setting

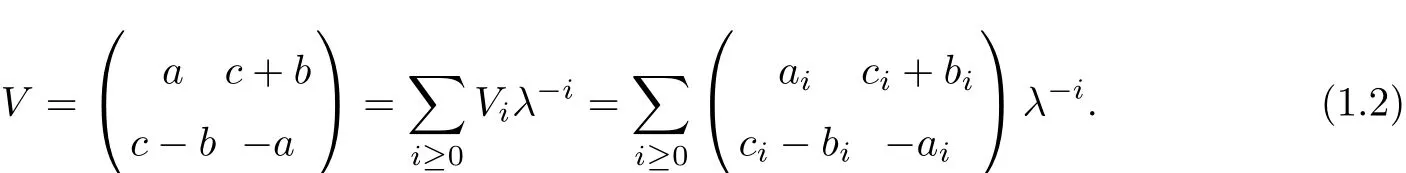
The stationary zero curvature equation Vx=[U,V]yields that

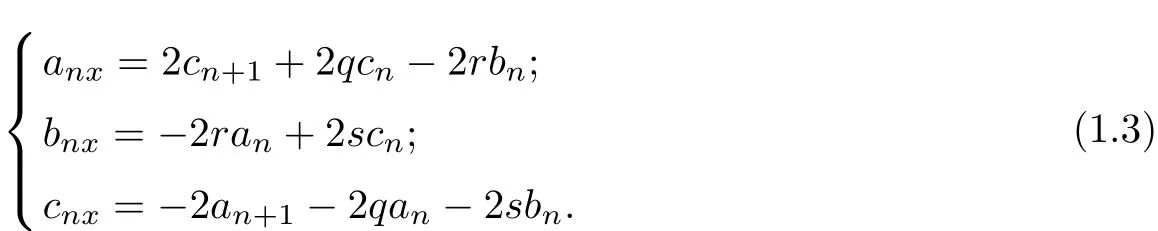
Choose the initial data

then we have

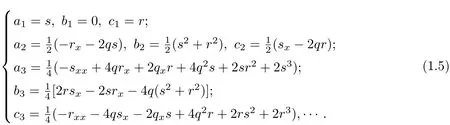
From the compatibility conditions of the following problems

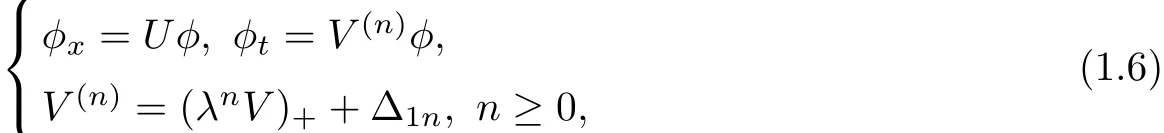
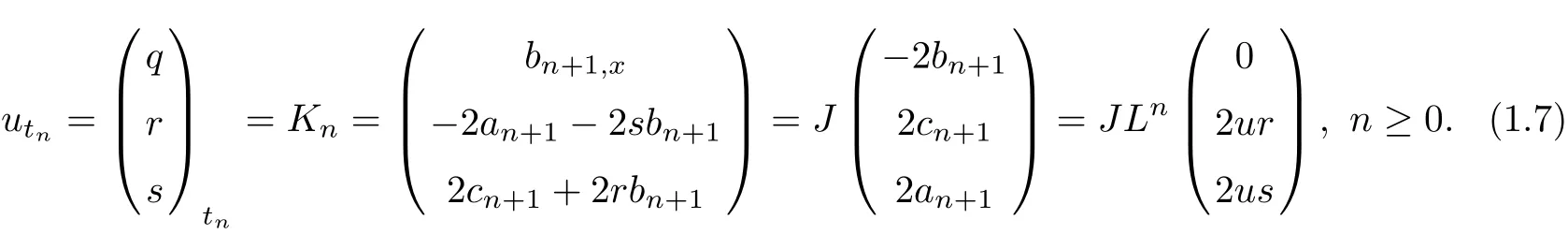
The Hamiltonian operator J,the hereditary recursion operator L and the Hamiltonian functions Hnas follows

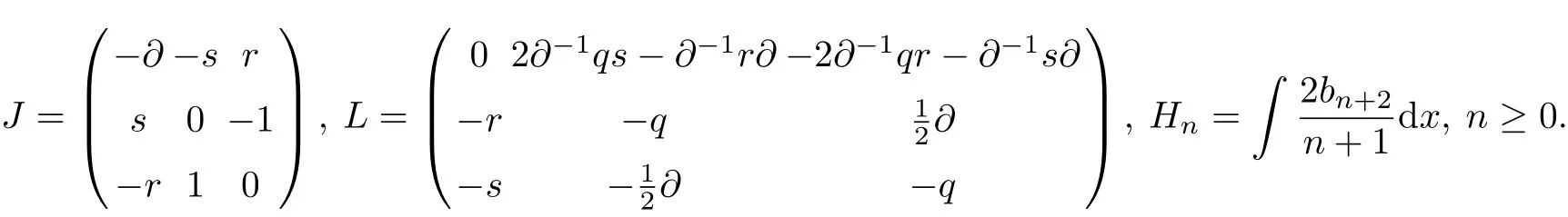
(1.8)

2.2Integrable Couplings

Let us begin with an enlarged spectral matrix

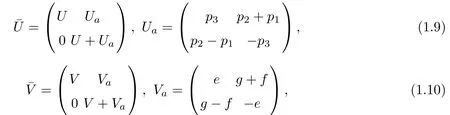
with the help of the corresponding enlarged stationary zero curvature equationˉVx=[ˉU,ˉV],we have

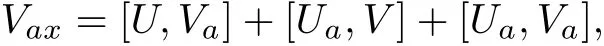
which generates

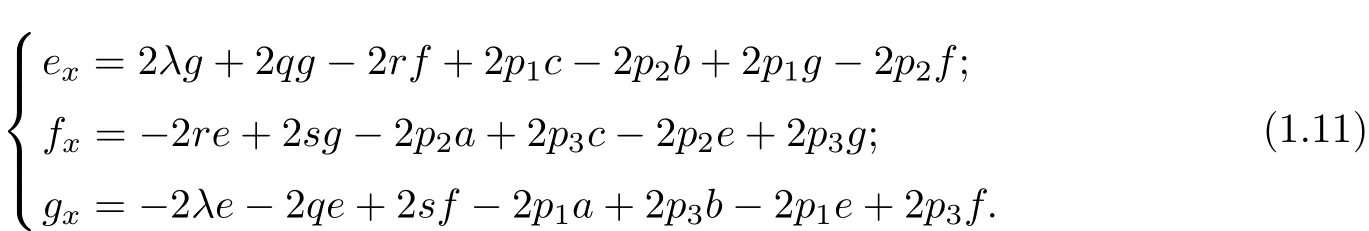
Setting

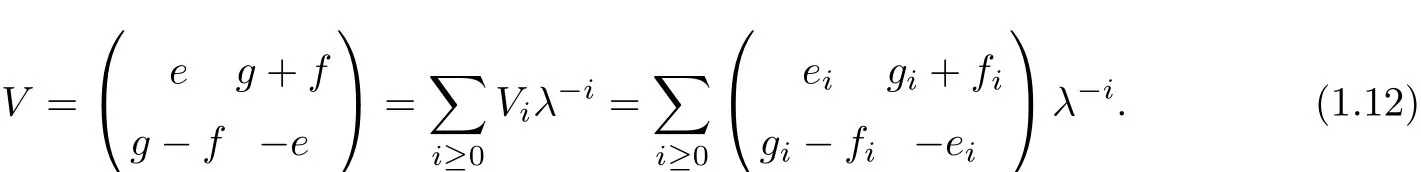
Then,the Eq(1.11)can be transformed into

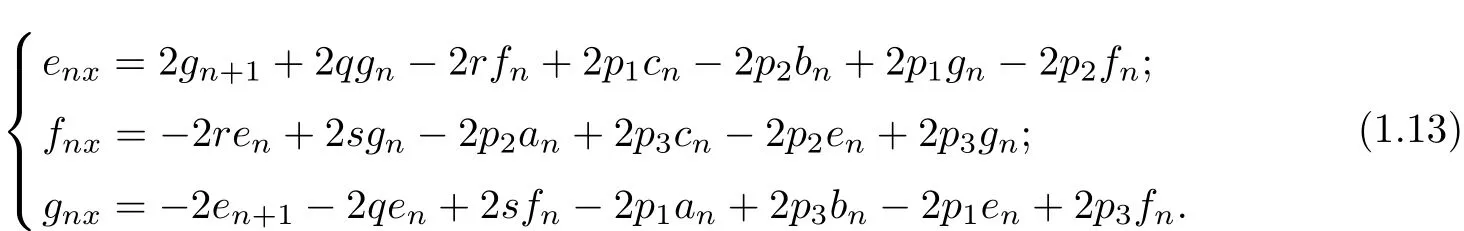
We choose the initial data

then we have

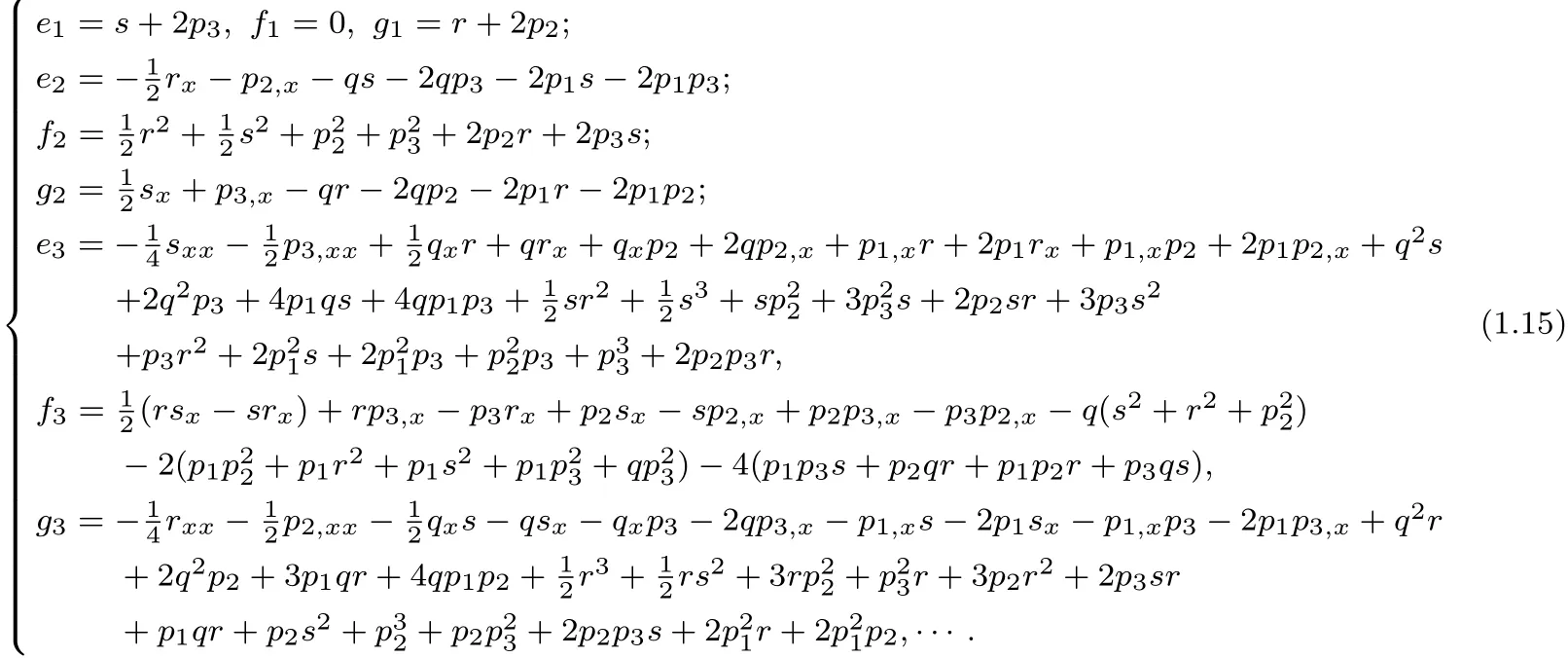
By using the zero curvature equation,

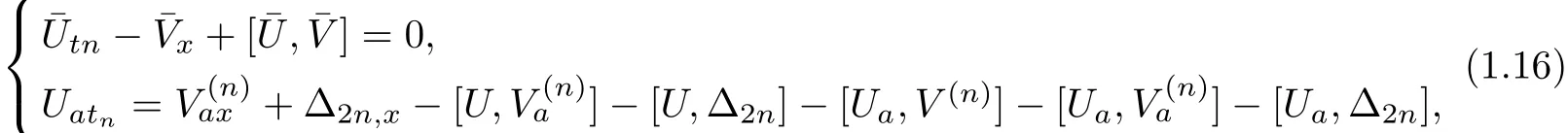
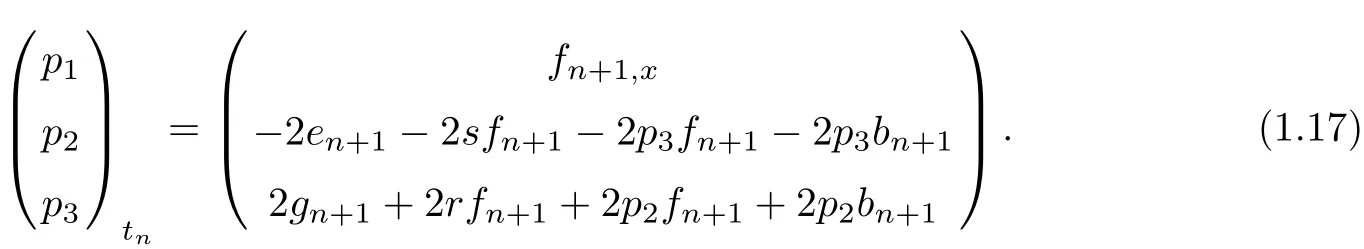
Then,we have the following results

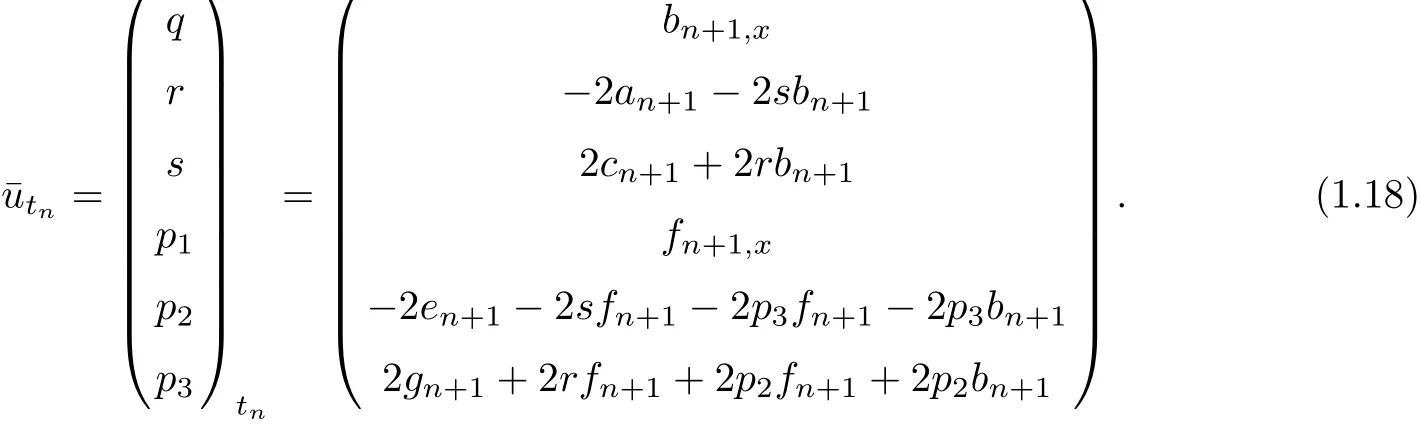
Obviously,when p1=p2=p3=0 in Eq(1.18),the above results become Eq(1.7).So we can say Eq(1.18)is the integrable couplings of Yang hierarchy.When n=2,the Eq(1.18)can reduced to b

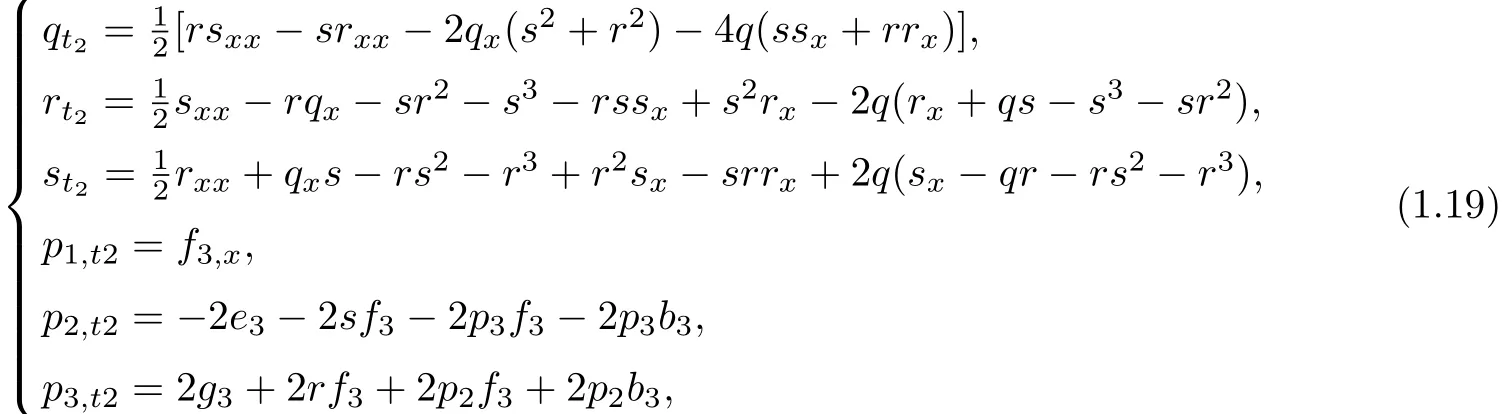
where

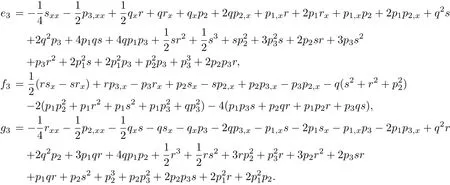
So,we can say that the system in(1.18)with n≥2 provide nonlinear integrable couplings of the Yang hierarchy.

§3.Hamiltonian Structures of the Integrable Couplings of the Yang Equations Hierarchy

To construct Hamiltonian structures of the integrable couplings obtained,we need to compute non-degenerate,symmetric and invariant bilinear forms on the following Lie algebra

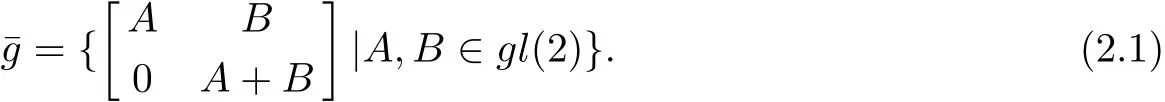
For computations convenience,we transform this Lie algebraˉg into a vector from through the mapping

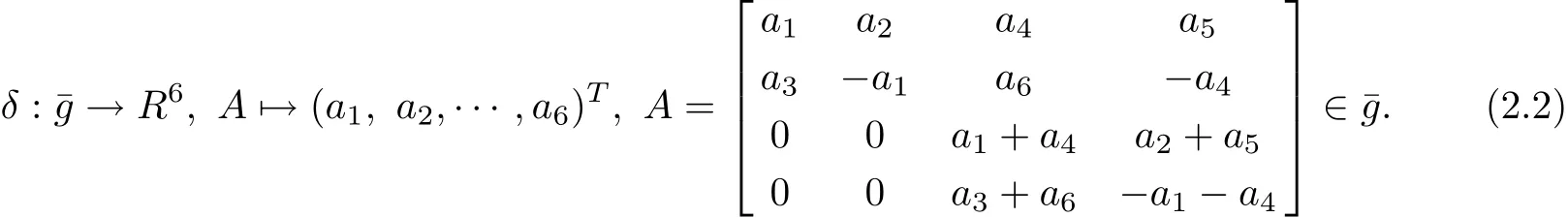
The mapping δ induces a Lie algebraic structure on R6,isomorphic to the matrix Lie algebra ˉg above.It is easy to see that the corresponding commutator[.,.]on R6is given by

where

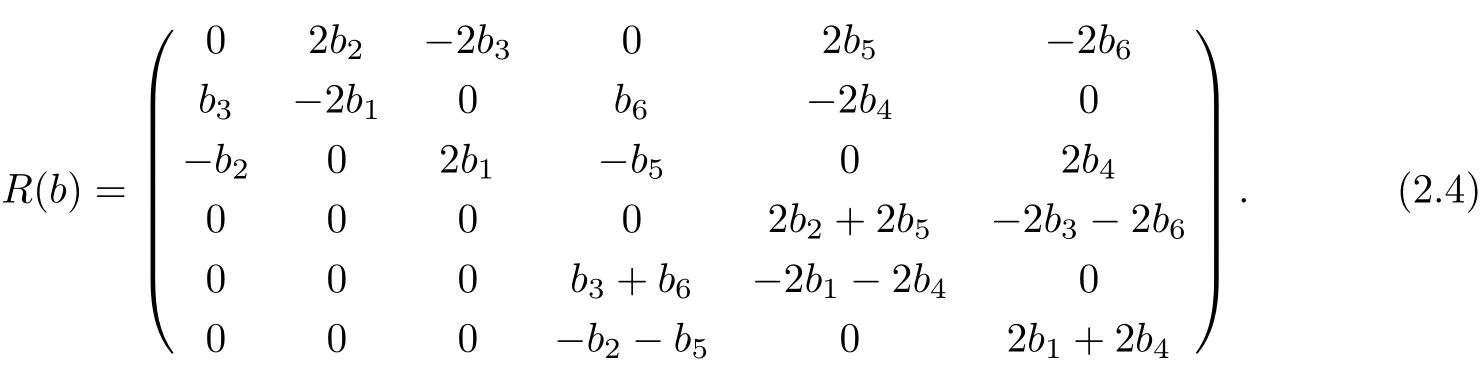
Def i ne a bilinear form on R6as follows

where F is a constant matrix,which is main idea by Zhang and Guo presented in 2005[5].

Then the symmetric property〈a,b〉=〈b,a〉and the ad-invariance property under the Lie product

requires that FT=F and

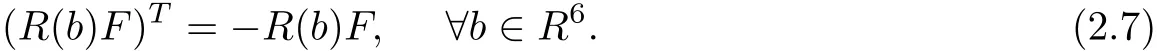
So we can obtain

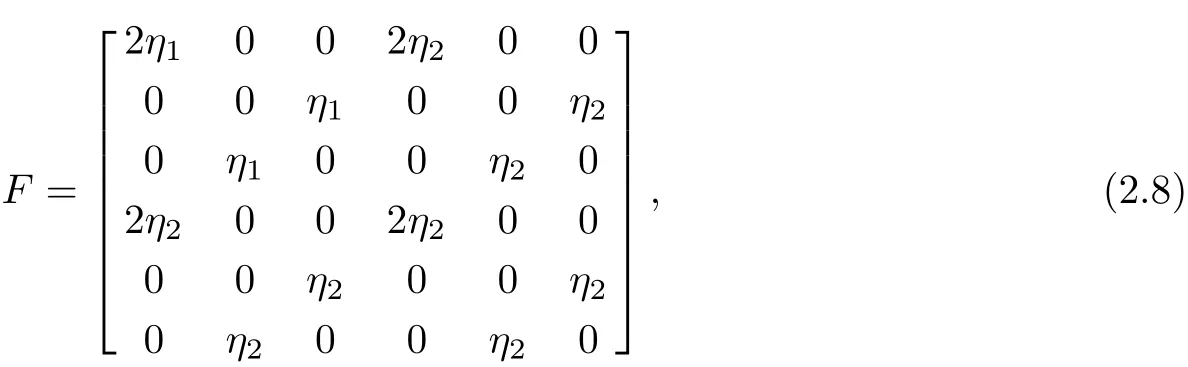
where η1and η2are arbitrary constants.Therefore,a bilinear form on the underlying Lie algebraˉg is def i ned by

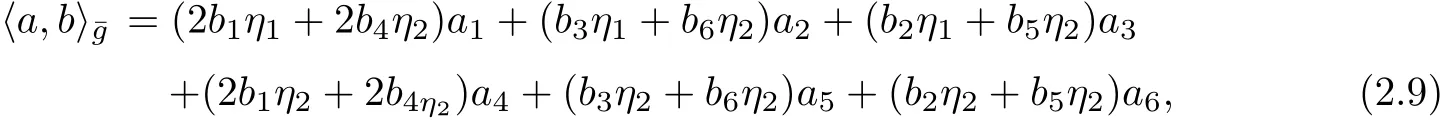
where

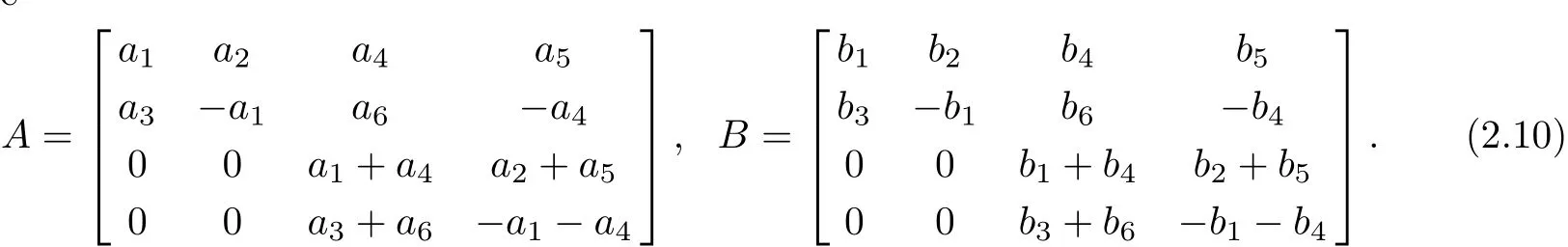
It is non-degenerate if and only if

Based on(2.12)and Eqs(1.9)～(1.10),we can easily compute that

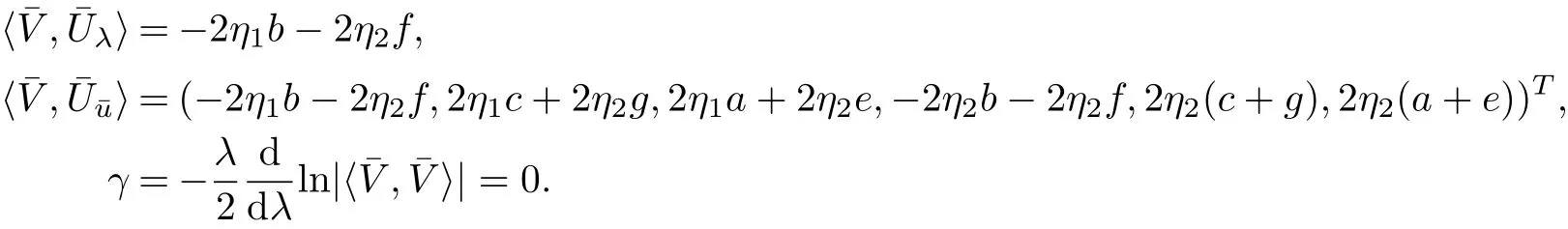
By applying the operator Γn+2to both sides of variational identity(6)

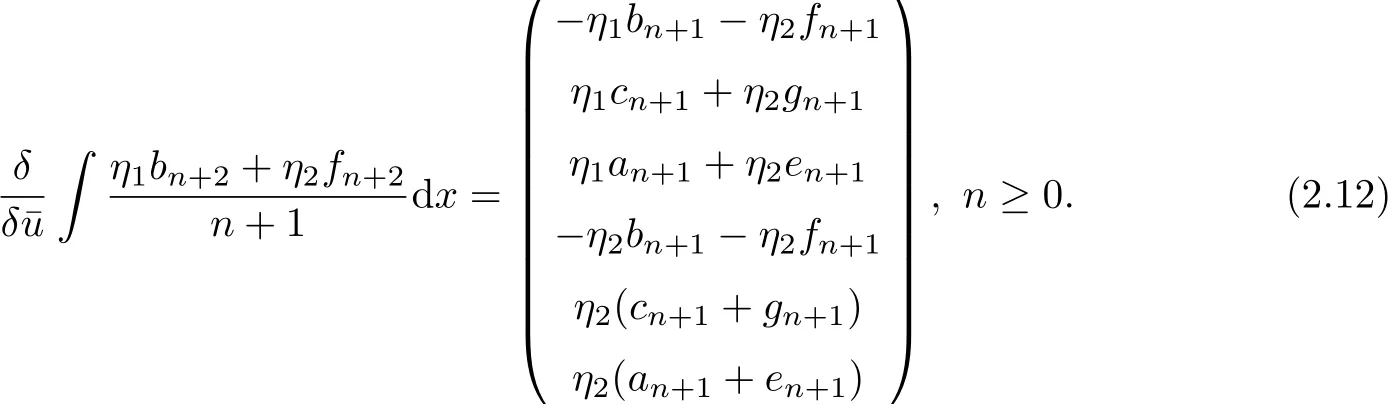
So we obtain that equation hierarchy(1.18)possess the Hamiltonian structures

where the Hamiltonian operatorˉJ and the Hamiltonian functional Hnare given by

and

With the help of(1.16),we can see a recursion relation

with

where L is given by(1.8)and

Up to now,we have already obtained Hamiltonian structure for integrable couplings of the Yang hierarchy.We must point out that by changing the nonlinear coupling terms of equations, more nonlinear integrable couplings with physical meaning can be obtained.So,with the help of this method,more meaningful results of other integrable hierarchies can be generated.

[References]

[1]MA Wen-xiu,FUCHSSTEINER B.Integrable theory of the perturbation equationa[J].Chaos,Solitons and Fractals,1996,7(8):1227-1250.

[2]MA Wen-xiu.Enlarging spectral problems to construct integrable couplings of soliton equations[J].Physics Letters A,2003,316(1-2):72-76.

[3]XIA Tie-cheng,ZHANG Gai-lian,FAN En-gui.New integrable couplings of generalized Kaup-Newell hierarchy and its Hamiltonian structures[J].Communications in Theoretical Physics,2011,56(1):1-4.

[4]LIU Yu-qing,CHEN Deng-yuan.The exact solutions to a Ragnisco-Tu hierarchy with self-consistent sources[J].Nonlinear Analysis,2011,74(16):5223-5237.

[5]MA Wen-Xiu,XU Xi-Xiang,ZHANG Yu-feng.Semi-direct sums of Lie algebras and discrete integrable couplings[J].Physics Letters A,2006,351(3):125-130.

[6]GUO Fu-kui,ZHANG Yu-feng.The quadratic-form identity for constructing the Hamiltonian structure of integrable systems[J].Journal of Physics A:Mathematical and General,2005,38(40):8537-8548.

[7]MA Wen-xiu.A Hamiltonian structure associated with a matrix spectral problem of arbitrary-order[J]. Physics Letters A,2007,367(6):473-477.

[8]GUO Fu-kui,ZHANG Yu-feng.The integrable coupling of the AKNS hierarchy and its Hamiltonian structure[J].Chaos,Solitons and Fractals,2007,32(5):1898-1902.

[9]MA Wen-xiu,GAO Liang.Coupling integrable couplings[J].Modern Physics Letters B,2009,23(15):1847-1860.

[10]MA Wen-xiu,ZHU Zuo-nong,Constructing nonlinear discrete integrable Hamiltonian couplings[J].Computers and Mathematics with Application,2010,60(9):2601-2608.

[11]MA Wen-xiu.Nonlinear conitnuous integrable Hamiltonian couplings[J].Applied Mathematics and Computation,2011,217(17):7238-7244.

[12]TU Gui-zhang.On liouville integrability of zero-curvature equations and the Yang hierarchy[J].1989,22(13): 2375-2392.

tion:35Q51

CLC number:O175.9Document code:A

1002–0462(2014)02–0180–09

date:2012-04-16

Supported by the Natural Science Foundation of China(11271008,61072147,11071159); Supported by the First-class Discipline of Universities in Shanghai;Supported by the Shanghai University Leading Academic Discipline Project(A13-0101-12-004)

Biography:WEI Han-yu(1982-),male,native of Zhoukou,Henan,a lecturer of Zhoukou Normal University, Ph.D.,engages in solitons and integrable systems.