李艷午, 劉鋼

(1.蕪湖職業(yè)技術(shù)學(xué)院,安徽 蕪湖 241000;2.宿州學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,安徽 宿州 234100)

半單環(huán)在環(huán)類(lèi)刻畫(huà)中的某些應(yīng)用

李艷午1, 劉鋼2

(1.蕪湖職業(yè)技術(shù)學(xué)院,安徽 蕪湖 241000;2.宿州學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,安徽 宿州 234100)

首先利用正則環(huán),對(duì)半單環(huán)進(jìn)行了一個(gè)新的刻畫(huà);然后,構(gòu)造了半單環(huán)成為單位正則環(huán)的一系列條件,在此基礎(chǔ)上對(duì)單位正則環(huán)進(jìn)行了半單環(huán)意義下的兩個(gè)刻畫(huà);最后,通過(guò)構(gòu)造Artin環(huán)到半單環(huán)的條件,將半單環(huán)的有關(guān)結(jié)論推廣到Artin環(huán)中.

半單環(huán);正則環(huán);單位正則環(huán);Artin環(huán)

1 引言

一個(gè)左R-模M叫做半單的,如果M 的任意R-子模都是M的直和項(xiàng);環(huán)R叫做半單環(huán),如果每個(gè)左R-模都是半單的.如同半單模在模論中扮演著十分重要的角色一樣,半單環(huán)在環(huán)論中占有重要的地位.因此,半單環(huán)越來(lái)越被一些代數(shù)工作者所重視,大部分環(huán)論的經(jīng)典著作[1-3]都對(duì)半單環(huán)進(jìn)行了深入探討和經(jīng)典刻畫(huà),一些重要的環(huán)類(lèi)也往往都與半單環(huán)有著密切的聯(lián)系,如SF-環(huán)[4].

環(huán)R中的一個(gè)元素a稱(chēng)為單位正則的,如果存在一個(gè)單位(即可逆元)u∈R,使a=aua;稱(chēng)R為單位正則環(huán),如果R的每個(gè)元素都是單位正則元[2].單位正則環(huán)與環(huán)的穩(wěn)定度和模的消去性都有著密切的關(guān)系,這是近年來(lái)繼正則環(huán)后又一個(gè)重要的環(huán)類(lèi),吸引著環(huán)論研究者的興趣.文章首先利用正則環(huán),對(duì)半單環(huán)進(jìn)行了一個(gè)新的刻畫(huà);然后,構(gòu)造了半單環(huán)成為單位正則環(huán)的一系列條件,在此基礎(chǔ)上對(duì)單位正則環(huán)進(jìn)行了半單環(huán)意義下的兩個(gè)刻畫(huà);最后,通過(guò)構(gòu)造Artin環(huán)到半單環(huán)的條件,將半單環(huán)的一系列結(jié)果推廣到Artin環(huán)中.

本文中的環(huán),都是有單位元的結(jié)合環(huán),模都是酉模;a∈R,l(a)表示元素a在環(huán)R中的左零化子,r(a)表示元素 a在環(huán) R中的右零化子.U(R)是環(huán) R的單位元素的集合.J(R)和Soc(RR)(Soc(RR))分別表示環(huán)R的Jacobson根和RR(RR)的基座.其余符號(hào)均參照文獻(xiàn) [1].

2 主要結(jié)果及證明

眾所周知,Artin半單環(huán)是正則環(huán)[5-6],但正則環(huán)不一定是半單環(huán);半單環(huán)既是Artin環(huán)又是Noether環(huán),但反之Artin環(huán)和Noether環(huán)又都不一定是半單環(huán),而下面的結(jié)果彌補(bǔ)了這一缺憾.

定理 1對(duì)于正則環(huán)R,下列各條等價(jià):

(1)R是半單環(huán);(2)R是Neother環(huán);(3)R是Artin環(huán).

證明(1)?(2),(1)?(3).由半單環(huán)的性質(zhì)易得.

(2)?(1).如果R是Neother環(huán),那么R滿(mǎn)足主左理想的升鏈條件.令S=Soc(RR),下面證明S=R.如果SR,那么存在R的極大主左理想I,使得S?I?R,并且I在R中是本質(zhì)的.又由于R是正則環(huán),所以存在e=e2∈R,使得I=Re,從而I是有限生成的.故正和列:是有限相關(guān)的,所以R/I是有限相關(guān)的平坦模.再根據(jù)文獻(xiàn)[8]中的TH3.16,R/I是投射左R-模,從而是RR的直和項(xiàng).而這與I在R中是本質(zhì)的相矛盾.所以,S=R.故,R是半單環(huán). (3)?(1).與(2)?(1)類(lèi)似,可證.

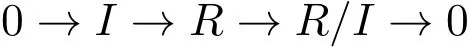
顯然,單位正則環(huán)都是正則環(huán),而反之不真.但是,根據(jù)文獻(xiàn)[7]中推論2.4,比正則環(huán)條件稍強(qiáng)的強(qiáng)正則環(huán)是單位正則環(huán).既然半單環(huán)都是正則環(huán),所以半單環(huán)距單位正則環(huán)僅一步之遙.下面的定理就是考慮極大左理想的性質(zhì),從幾條不同的渠道鋪設(shè)由半單環(huán)到單位正則環(huán)的路徑.

定理 2一個(gè)半單環(huán)R,如果又滿(mǎn)足下列條件之一:

(1)R的每個(gè)極大左理想都是理想;

(2)R的每個(gè)極大左理想在R中都是本質(zhì)的;

(3)R的每個(gè)極大左(右)理想都是廣義弱理想.

那么,R是單位正則環(huán).

證明首先由半單環(huán)的正則性知,環(huán)R是正則的.

如果條件(3)成立,那么根據(jù)文獻(xiàn)[9]中定理11,可證環(huán)R是強(qiáng)正則環(huán),故R是單位正則環(huán).

如果aR+bR=R,存在x∈R使得a+bx是一個(gè)單位,那么稱(chēng)環(huán)R具有穩(wěn)定度1(見(jiàn)文獻(xiàn)[2]).下面就由半單環(huán)在一定條件下的單位正則性,導(dǎo)出其具有穩(wěn)定度1的性質(zhì).

推論 1一個(gè)半單環(huán)R,如果又滿(mǎn)足下列條件之一:

(1)R的每個(gè)極大左理想都是理想;

(2)R的每個(gè)極大左理想在R中都是本質(zhì)的;

(3)R的每個(gè)極大左(右)理想都是廣義弱理想;

那么,R具有穩(wěn)定度1.

證明首先,根據(jù)定理2知環(huán)R是單位正則環(huán).令aR+bR=R,a,b∈R,則對(duì)某個(gè)J,有

進(jìn)一步,令K={r∈R|ar=0},則有RR=K⊕L,這里L(fēng)～=aR,再根據(jù)文獻(xiàn)[2]中定理4.1,知K～=J.因此,存在c∈R,使得cL=0,而且由c所決定的左乘導(dǎo)出了KJ上的一個(gè)同構(gòu).由于cR=J≤bR,所以存在某個(gè) y∈R,使得c=by.同理,由a所決定的左乘導(dǎo)出了LaR上的一個(gè)同構(gòu).因?yàn)閍K=cL=0,由此推出由a+c所決定的左乘導(dǎo)出了L⊕K=RRaR⊕J=RR上的一個(gè)同構(gòu).所以,a+by=a+c是R中的一個(gè)單位,即環(huán)R具有穩(wěn)定度1.

下面的定理將從有限生成投射模的消去性質(zhì),對(duì)單位正則環(huán)進(jìn)行有限生成投射模消去意義上的刻畫(huà).

定理 3設(shè) R是一個(gè)半單環(huán),則 R是單位正則環(huán)當(dāng)且僅當(dāng)對(duì)所有有限生成投射 R-模A,B,C,由A⊕B～=A⊕C都可以推出B～=C.

證明一方面,如果對(duì)所有有限生成投射R-模A,B,C,由A⊕B～=A⊕C都可以推出B～=C,那么根據(jù)文獻(xiàn)[2]中定理4.1,由模的這種消去性推出了R的單位正則性.

另一方面,如果R是半單的單位正則環(huán),令A(yù),B,C是有限生成投射左R-模,并且A⊕B～= A⊕C,那存在正整數(shù)n,使得A是nRR的一個(gè)直和項(xiàng),這里nRR⊕B～=nRR⊕C.通過(guò)歸納,可以證明n=1的情形.假設(shè)RR⊕B～=RR⊕C,根據(jù)文獻(xiàn)[2]中定理2.8,給出了一個(gè)分解RR=R1⊕R2,B=B1⊕B2,使得

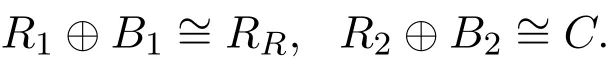
由于R1⊕B1～=RR=R1⊕R2,所以B1～=R2,于是

推論 2設(shè)R是有穩(wěn)定度1的半單環(huán),M是R上的有限生成投射模,則EndR(M)是單位正則環(huán).

證明如果R是有穩(wěn)定度1的半單環(huán),那么由R的正則性知對(duì)任意的a∈R,存在x∈R使得a=axa.顯然,aR+(1?ax)R=R,于是存在y∈R使得a+(1?ax)y是一個(gè)單位,從而存在u∈R使得[a+(1?ax)y]u=1.所以,

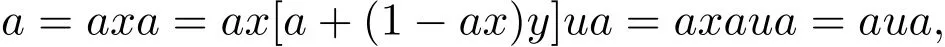
即R是單位正則環(huán).最后,根據(jù)文獻(xiàn)[2]中推論4.7,即證R(M)是單位正則環(huán).

定理 4設(shè)R是一個(gè)半單環(huán),I是R的雙邊理想,則R是單位正則環(huán)當(dāng)且僅當(dāng)下列兩條同時(shí)成立:

(1)R/I是單位正則環(huán)

證明一方面,如果R是單位正則環(huán),那么根據(jù)單位正則環(huán)的性質(zhì)定理即[2]中定理4.1,即可得到結(jié)論(1)和結(jié)論(2).

另一方面,如果環(huán) R滿(mǎn)足條件 (1)和條件 (2).那么根據(jù)半單環(huán)的正則性,給定冪等元a,b∈R使得aRbR,由條件(1)可得(R/J)～=(R/J),因此

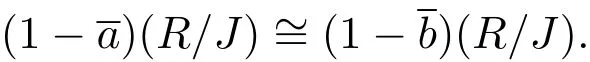
根據(jù)文獻(xiàn)[2]中命題2.19,存在分解

使得A1～=B1而A2=A2J,B2=B2J.于是,存在冪等元e,f∈R使得

而使

那么e,f∈J,并且(1?e)R～=(1?f)R,從而根據(jù)條件(2)得eR～=fR,于是(1?a)R～=(1?b)R,因此R是單位正則環(huán).

定理 5設(shè)R是左Artin環(huán),則R只要滿(mǎn)足下列條件之一:

(1)不包含非零的冪零左理想;

(2)對(duì)任意x∈R,xRx=0?x=0.

就有:

(a)環(huán)R的總體維數(shù)等于0;

(b)對(duì)任意左R-模M,M 既是投射模又是內(nèi)射模;

(c)由左R-模構(gòu)成的短正和列都可裂;

(d)環(huán)R的詣零根等于零;

(e)存在R的有限個(gè)雙邊理想Ri,i=1,2,···,n,n<∞,使得

證明根據(jù)文獻(xiàn)[1]中習(xí)題13,8(2)知,當(dāng)R是左Artin環(huán)并且滿(mǎn)足條件(1)和條件(2)時(shí),R就是半單環(huán).再根據(jù)文獻(xiàn)[3]中定理 12和定理13對(duì)半單環(huán)的經(jīng)典刻畫(huà),即可得到結(jié)論 (a)-(e).與半單純環(huán)關(guān)系密切的環(huán)是本原環(huán),即 J(R)=0的環(huán),它可以看成是半單純環(huán)概念的推廣,它是除環(huán)上的線性空間的線性變換完全環(huán)的一個(gè)稠密子環(huán).根據(jù)文獻(xiàn)[10]中推論2.4.14,半單環(huán)等價(jià)于半本原的阿丁環(huán),所以有:

注 1把定理[7]中的條件(1)和條件(2)改為R是半本原的,同樣得到結(jié)論(a)-(e).

[1]Anderson F W,Fuller K R.Rings and Categories of Modules[M].Berlin Heidelberg:Springer-Verlag,1974.

[2]Goodearl K R.Von Neumann Regular Rings[M].2nd ed.Florida:Krieger Publishing Company Malabar, 1991.

[3]周伯塤.同調(diào)代數(shù)[M].北京:科學(xué)出版社,1998.

[4]李艷午,程海霞.SF-環(huán)的內(nèi)射性[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2012,28(1):17-24.

[5]Faith C.Algebra II:Rings Theory[M].Berlin Heidelberg,Springer-Verlag,1976.

[6]Fisher J.W.Von Neumann Regular Rings Versus V-rings,in“Rings Theory Proceedings of the Oklahoma Conference”[C]//Lecture Notes in Pure and Appl.Math..New York:Dekker,1974(7):101-119.

[7]李艷午,儲(chǔ)茂權(quán).Morphic Rings and regular Rings[J].安徽師范大學(xué)學(xué)報(bào):自然科學(xué)版,2010,33(4):313-316.

[8]Rege M B.On Von Neumann regular rings and SF-rings[J].Math.Japonica,1986,36(1):927-936.

[9]周海燕,王小東.Von Neumann正則環(huán)和左SF-環(huán)[J].數(shù)學(xué)研究與評(píng)論,2004,24(4):679-683.

[10]陳家鼐.環(huán)與模[M].北京:北京師范學(xué)院出版社,1989.

Some applications about semisimple rings in the characterization of rings

Li Yanwu1,Liu Gang2
(1.Wuhu Vocational College of Technology,Wuhu 241000,China; 2.College of mathematics and statistics in Suzhou institute,Suzhou 234100,China)

Firstly,a new characterization of semisimple rings was obtained in In the sense of regular rings. Secondly,we constructed a series of conditions which from semisimple rings to unit regular rings and on which two characterizations were obtained about unit regular rings in terms of semisiple rings.Finally,by constructing the conditions that from Artin rings to semisimple rings,a series of results about semisimple ring were pushed to Artin rings.

semisimple rings,regular rings,unit regular rings,Artin rings

O153.3

A

1008-5513(2014)02-0149-05

10.3969/j.issn.1008-5513.2014.02.005

2013-12-27.

安徽省2013年省級(jí)自然科學(xué)研究項(xiàng)目(KJ2013B348);2011年度安徽省教育科學(xué)規(guī)劃項(xiàng)目(JG11372);蕪湖職業(yè)技術(shù)學(xué)院2013年院級(jí)教學(xué)研究項(xiàng)目.

李艷午(1975-),碩士,副教授,研究方向:環(huán)論與同調(diào)代數(shù).

2010 MSC:16G10,16E10