LI Ping-run

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

A Class of Singular Integral Equation of Convolution Type with csc(τ?θ)Kernel

LI Ping-run

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

In this paper,we propose and discuss a class of singular integral equation of convolution type with csc(τ?θ)kernel in class L2[?π,π].Using discrete Fourier transform and the lemma,this kind of equations is transformed to discrete system of equations,and then we obtain the solvable conditions and the explicit solutions in class L2[?π,π].

singular integral equation;convolution type;csc(τ?θ)kernel

§1.Introduction and Def i nition

In the theory of integral equation,integral equation of convolution type and singular integral equation are two important classes of equations,which have been deeply studied by many mathematical researchers at home and abroad,there is already a rather complete theory system. This theory has been widely used in practical applications such as engineering mechanics, fracture mechanics,elastic mechanics(see[1-10]).In 1978,the solvability of integral equation with Cauchy kernel and convolution kernel has been studied by Duduchava R V,which proposed and discussed the following singular integral equation of Wiener-Hopf type with convolution kernel and Cauchy kernel

where a,cj,dj∈R,k0(t)∈L1(?∞,+∞)and g(t),φ(t)∈L2(?∞,+∞),he discussed the solvable Noether theory of equation(1.1)(see[11]).In 1980,Lu Jianke studied the singularintegral equation with cosecant csc(t?t0)/a(see[12-13]).In 1984,Lu Jianke proposed a general method to solve some classes of singular integral equations with convolution kernel and Cauchy kernel,in which the convolution kernel has discontinuous property,that is to transform those integral equations to Riemann boundary value problem by using Fourier transform(see [14]).

Based on the above discussion,we propose and solve a class of singular integral equation with csc(τ?θ)kernel and convolution kernel in class L2[?π,π](the def i nition of L2[?π,π]used in[15]),we transform this kind of integral equation to discrete system of equations.Therefore, we obtain the conditions of solvability and the explicit expression of general solution.

then w,w?1are called the discrete Fourier transform operator and the discrete inverse Fourier transform operator respectively.

For simplif i cation,we denote as w?1[F(θ)]=fk(k=0,±1,±2···).It is easy to observe that for any two functions F(θ),G(θ)with period 2π,we have w?1[F?G(θ)]=fkgk,where gk=w?1[G(θ)].

§2.Lemma and Its Proof

The following lemma is important to our paper,and it is proposed f i rstly in this paper.

LemmaLet F(θ)∈L2[?π,π],then

(1)w?1(SF(θ))=2fkρksgnk,w?1(?SF(θ))=?2f?kρksgnk;

(2)SF(θ)∈L2[?π,π],w?1(?SF(θ))∈l2[?π,π](for the def i nition of l2[?π,π]see[16]).

Proof(1)From

we have

Using the Extended Residue Theorem(see[16]),when k≥0,we have

when k＜0,we obtain

Therefore,when k≥0,we have

When k＜0,we get

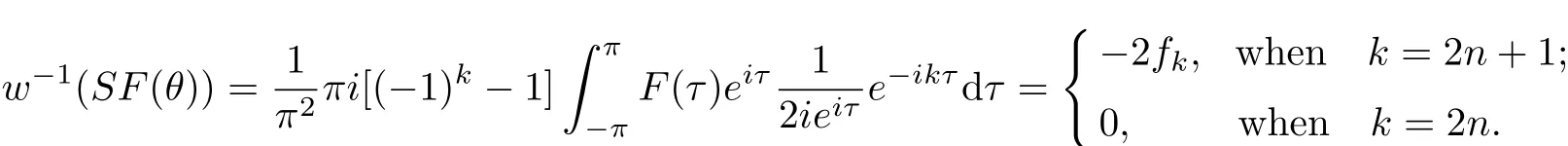
Hence,we have

Similarly,the second equality can proved also.

(2)By the Riesz′s theory(see[17]),we have||SF(θ)||2≤C||F(θ)||2,where C is a constant. Since F(θ)∈L2[?π,π],we obtain SF(θ)∈L2[?π,π].

It is also obvious for the second conclusion in(2).

§3.Singular Integral Equation of Convolution Type with csc(τ?θ)Kernel

In this section,we consider the following equation with csc(τ?θ)kernel

where

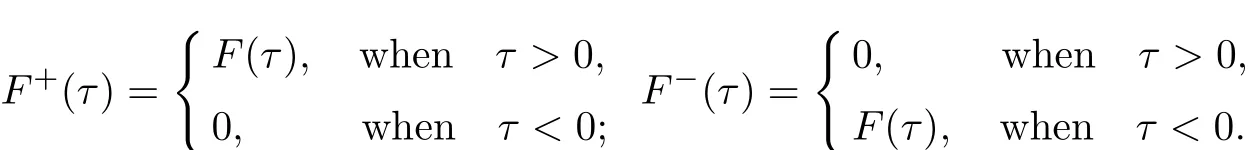
a,bj,cj(j=1,2)are real constants with bjnot all equal to zero simultaneously,Kj(θ)(j= 1,2),G(θ)∈L2[?π,π]are given functions and F(θ)is the unknown function but is required to be even in this paper.Applying w?1to both sides of equation(I),we obtain

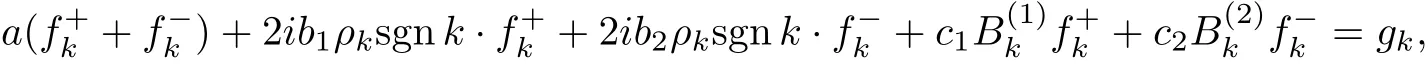
where fk±=w?1(F±),Bk(j)=w?1Kj,gk=w?1G(j=1,2).

Since F(θ)is an even function,we have

Therefore,we get

Replacing k by?k in(3.1),then Next,we solve the system of equations(3.3)with unknown number sequence(f,)and

denote

Then

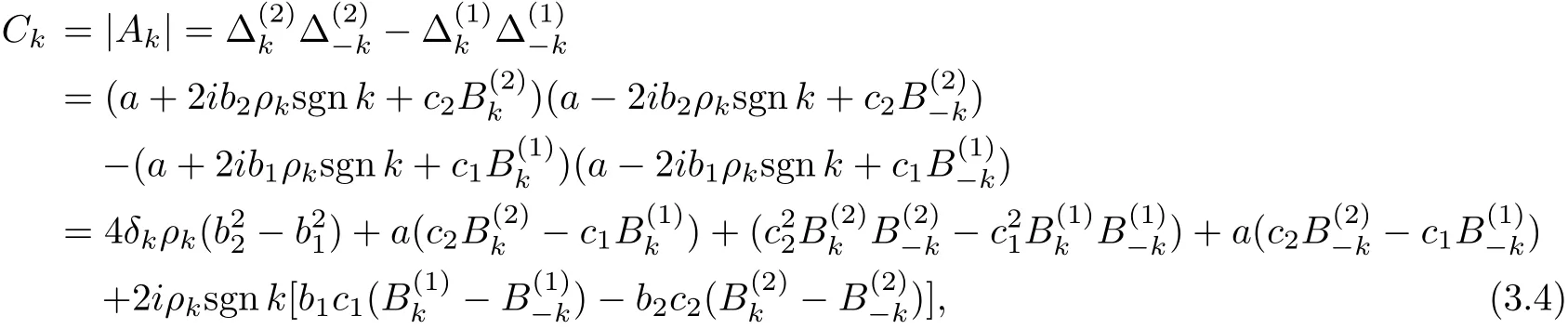
where

When|k|≤k0,we have the following results.

(1)If Ck/=0,then Ak/=0(k=0,±1,···,±k0),the system of equations(3.3)has a solution (,f).

(2)If Ck/=0 and gk=0(k=0,±1,···,±k0),then the system of equations(3.3)has only zero solution.

(3)If Cnj=0 and RAnj=RBnj(1≤j≤p,RA is order of matrix A),the system of equations(3.3)has in fi nite solutions()(1≤j≤p,?k0≤nj≤k0). (4)If Cn′j=0 and RAn′j/=RBn′jfor j=0,1,2,···,p1(?k0≤n′j≤k0),then the system of equations(3.3)has no solution.

(5)If Cn′j′=0 and/=RBn′j′for j=0,1,2,···,p2(?k0≤n′j≤k0),then the conditions of solvability=0,i.e.,G(±θ)e±in′j′θdθ=0 or

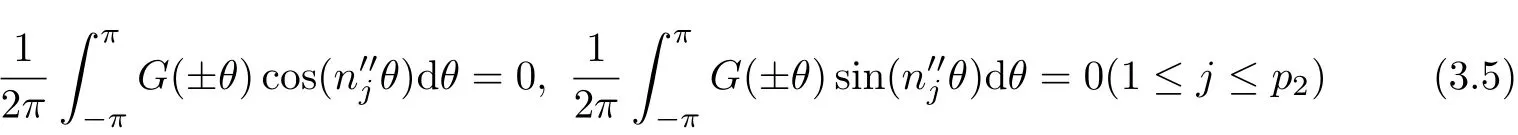
must be augmented.Therefore,

(1)The system of equations(3.3)has the unique solution.

(2)The system of equations(3.3)has in fi nite solutions()(1≤j≤p,?k0≤nj≤k0).

(3)The system of equations(3.3)has no solution.

(4)The system of equations(3.3)has in fi nite solutions when(3.5)satis fi ed.

In the following discussion,we consider the homogeneous case of equation(I)(i.e.,G(θ)=0), then the system of equations(3.3)is readily reduced to

We know that,from the above discussion,there must be|k|≤k0;if|k|＞k0,then Ck/=0,in this case,(3.6)has only the zero solution.Then there exist k=n1,n2,···,npsuch that Ck=0, therefore,we obtain that fn?j,f??nj(j=1,2,···,p)are constants and fnj(j=1,2,···,p)are also constants.For the other k(?k0≤k≤k0,k/=n1,···,np),we have fk?=f??k=0 and hence fk=0.And then F(θ)is linearly represented by ein1θ,ein2θ,···,einpθ,i.e.,

where ein1θ,ein2θ,···,einpθ(ni/=njwhen i/=j)are linearly independent and the linear independence can be proved by using Vandermonde determinant in Linear Algebra.Therefore,for homogeneous equation(i.e.,G(θ)=0),the system of equations(3.3)has linearly independent solutions ein1θ,ein2θ,···,einpθ.

From

we obtain

In summary,we get the solvability theorem of equation(I).

TheoremUnder the supposition

(1)If Ck/=0(k=0,±1,···),then equation(I)has unique solution in L2[?π,π]and the solution is

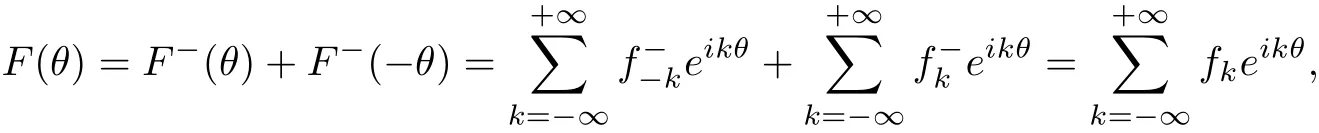
Some classes of singular integral equations such as singular integral equation of dual type with csc(τ?θ)kernel,Wiener-Hopf type equations and singular integral equation with csc(τ?θ) kernel and Hilbert kernel,can be solved by using the above methods.Hence the general solutions of those equations as well as the conditions of solvability in class L2[?π,π]can be also obtained. The details will be omitted here(see[18-19]).

[1]LU Jian-ke.Boundary Value Problems for Analytic Functions[M].Singapore:World Sci,2004.

[2]DU Jin-yuan,LU Jian-ke.On a class of singular integral equations with translations[J].Chinese Annals of Mathematics.1990,11B(1):105-117.

[3]LU Jian-ke.Some classes boundary value problems and singular integral equations with a transformation[J]. Advances in Mathematics,1994,23(5):424-431.

[4]ZHONG Shou-guo.Several types of formulas to interchanging order of integration for singular integrals of higher order on the real axis[J].J of Math,2000,20(3):355-358.

[5]LI Ping-run.Method of solutions for some kinds of singular integral equations of convolution type with both ref l ection and translation shift[J].Chinese Quarterly Journal of Mathematics,2014,29(1):107-115.

[6]LI Ping-run.On method of solution of non-normal type for one kind of singular integral dif f erential equations with both convolution kernel and Cauchy kernel[J].Journal of Systems Science and Mathematical Sciences, 2014,34(3):352-361.

[7]LITVINCHUK Gueorgui-Si.Singular Integral Equations and Boundary Value Problems with Shift[M]. Moscow:Nauka Press,1978.

[8]DU Jian-yuan,XU Ma,ZHANG Zhong-xiang.Boundary behavior of Cauchy-type integrals in clif f ord analysis[J].Acta Math Sci,2009,29B(1):210-224.

[9]TAKAHIKO Nakazi,TAKANORI Yamamoto.Normal singular integral operators with Cauchy kernel on[J]. Integral Equations and Operator Theory,2014,78:233-248.

[10]LU Jian-ke,SHEN Yong-xiang.Singular integral equation with convolution kernel and Cauchy kernel in class[J].Chinese Annals of Mathematics,1992,13A(6):672-680.

[11]DUDUCHAVA R V.Integral operators of convolution type with discontinuous coefficients[J].Math:Nachr, 1978,(79):75-98.

[12]LU Jian-ke,WANG Xiao-lin.A singular integral equation with kernel[J].Wuhan University Journal of Natural Sciences,1980,(4):22-30.

[13]LU Jian-ke,WANG Xiao-lin.A inversion formula of singular integral with kernel[J].Mathematics Research Report(Wuhan University),1980,5:51-58.

[14]LU Jian-ke.On methods of solution for some kinds of singular integral with convolution[J].Chin Ann of Math,1987,8B(1):97-108.

[15]EELBODE Dvan-Mau,SOMMEN Fe.The inverse Radon transform and the fundamental solution of the hyperbolic Dirac equation[J].Math Z,2004,247:733-745.

[16]LI Ping-run.Integral equations containing both cosecant and convolution kernel with periodicity[J].J Sys Sci and Math Scis,2010,30(8):1148-1155.

[17]LI Ping-run.On method of solution for two classes of equations of convolution type with harmonic singular operator[J].Journal of Systems Science and Mathematical Sciences,2013,33(7):854-861.

[18]HUANG Sha,QIAO Yu-ying,WEN Guo-cun.Real and Complex Clif f ord Analysis[M].New York:Springer, 2005.

[19]XU Yong-jia.Some properties of singular integral operators on the opening curve[J].China Mathematics, 2007,37A(2):229-248.

tion:30E25,45E10

1002–0462(2014)04–0620–07

date:2013-09-16

Supported by the Qufu Normal University Youth Fund(XJ201218)

Biography:LI Ping-run(1966-),male,native of Yanzhou,Shandong,an associate professor of Qufu Normal University,Ph.D.,engages in the boundary value problem of analytic function and singular integral equation.

CLC number:O175.5,O175.8Document code:A