李恒燕,韓 笑,劉天寶

(1. 華北水利水電學院 數(shù)學與信息科學學院,鄭州 450011;2. 吉林大學 數(shù)學學院,長春 130012;3. 空軍航空大學 數(shù)學教研室,長春 130022)

目前,應用最廣泛的求非線性方程行波解[1]的方法就是tanh方法和(G′/G)擴展法[2]. 本文運用tanh方法和(G′/G)擴展法求一般的非線性方程行波解,通過對解最后表達形式的分析,表明兩種方法具有一致性. tanh方法是最早用于求行波解的方法[3-5];(G′/G)擴展法是建立在tanh方法基礎上對行波解進行更一般形式的討論[6-11],引進了更多的未知系數(shù),得到了更廣泛的行波解.

考慮如下一般的非線性波動方程:

utt+αuxx+βu+γu3=0,

(1)

其中:α<0;β,γ為非零參數(shù).

1 (G′/G)拓展法

假設u(x,t)=U(ξ),ξ=kx+wt,則有

ux=kU′,ut=wU′,uxx=k2U″,utt=w2U″.

(2)

將式(2)代入非線性波動方程(1),可得

w2U″+αk2U″+βU+U3=0.

(3)

可將U(ξ)表示為一個關于(G′/G)的多項式:

(4)

其中G=G(ξ)滿足G″+λG′+μG=0. 則有

(5)

將式(5)代入式(3),并將代入后式(3)中含有(G′/G)的微分項中(G′/G)的最高次項與不含有(G′/G)的微分項中(G′/G)的最高次項找出來,建立等式可得n+2=3n,解得n=1,即

(6)

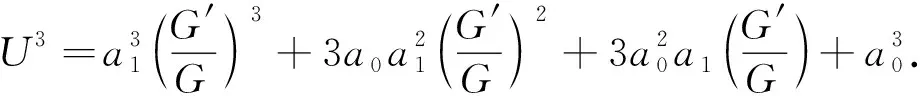
(7)

將式(6),(7)代入式(3),可得一個關于(G′/G)的非線性方程,再將所有系數(shù)整理并將每個系數(shù)均令為0,可得

(8)

將方程組(8)應用Math軟件可得4組解：

(9)

將式(9)各組解分別代入式(3),即可得到該非線性方程的行波解.

第一組解求出的行波解是：當λ2-4u>0時,

(10)

則有

其中

(12)

當λ2-4u<0時,

(13)

其中ξ為式(12). 當λ2-4u=0時,

(15)

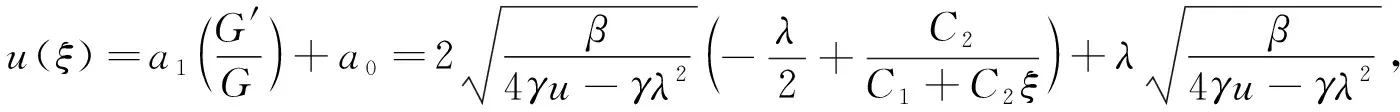
(16)

其中ξ為式(12).

第二組解求出的行波解是：當λ2-4u>0 時,由式(10),則有

(17)

其中

(18)

當λ2-4u<0時,由式(13),有式(14),其中ξ為式(18). 當λ2-4u=0時,由式(15),有式(16),其中ξ為式(18).

第三組解求出的行波解是：當λ2-4u>0時,由式(10),有

其中ξ為式(12). 當λ2-4u<0時,由式(13),有

其中ξ為式(12). 當λ2-4u=0時,由式(15),有

(21)

其中ξ為式(12).

第四組解求出的行波解是：當λ2-4u>0時,由式(10),有式(19),其中ξ為式(18). 當λ2-4u<0 時,由式(13),有式(20),其中ξ為式(18). 當λ2-4u=0時,由式(15),有式(21),其中ξ為式(18).

2 tanh函數(shù)法

假設u(x,t)=U(ξ),ξ=kx+λt,則有

ux=kU′,ut=λU′,uxx=k2U″,utt=λ2U″.

(22)

將式(22)代入非線性波動方程(1),可得

λ2U″+αk2U″+βU+γU3=0.

(23)

可假設U(ξ)為一個關于w的多項式:

(24)

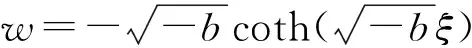
(25)

將式(24),(25)代入式(9),即可得到一個線性方程,應用齊次平衡原理,可得一個關于M的方程：4+M-2=3M,解得M=1. 又由式(24),可得U(ξ)=a0+a1w+b1w-1. 顯然可得

(26)

式(26)代入式(9)即可得一個關于w的代數(shù)方程:

將方程(27)的所有系數(shù)整理并將每個系數(shù)均令為0,可得

(28)

將方程組(28)應用Math軟件可得8組解：

(29)

計算得到的1～4組解顯然與(G′/G)展開法得到的解一致,而由于本文推廣了雙曲正切法,從而比(G′/G)方法多得到了4組解,即得到了b1≠0的解.

將式(29)的各組解代入式(23),即可得到該非線性方程的行波解. 分析對應的a0,a1,b1,對于方程中不同的參數(shù)γ可得相應的解為: 當γ<0,即b<0時,對應的行波解表達式如下:

當γ>0,即b>0時,對應的行波解表達式如下:

當γ<0,特別取α=-1,β=2,γ=-1時,常數(shù)b=-4,對應雙曲正切解和雙曲余切解可得行波解的圖像.

3 一致性分析

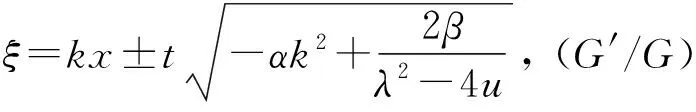
用tanh方法求出的行波解形式為

通過上述推導與分析得到了統(tǒng)一的結果,可見(G′/G)拓展法和tanh函數(shù)方法在本質上是一致的,此外利用擴展的雙曲正切函數(shù)法可以得到更多的精確形式行波解.

[1] Parkes E J. A Note on Travelling-Wave Solutions to Lax’s Seventh-Order KdV Equation [J]. Appl Math Comput,2009,215(2): 864-865.

[2] Wazwaz A M. New Travelling Wave Solutions of Different Physical Structures to Generalized BBM Equation [J]. Phys Lett A,2006,355(4/5): 358-362.

[3] Lax P D. Integrals of Nonlinear Equations of Evolution and Solitary Waves [J]. Commun Pure Appl Math,1968,21: 467-490.

[4] LOU Sen-yue,HUANG Guo-xiang,RUAN Hang-yu. Exact Solitary Waves in a Convecting Fluid [J]. J Phys A: Math Gen,1991,24(11): L587-L590.

[5] Wazwaz A M,Helal M A. Nonlinear Variants of the BBM Equation with Compact and Noncompact Physical Structures [J]. Chaos,Solitons &Fractals,2005,26(3): 767-776.

[6] Kudryashow N A. Meromorphic Solutions of Nonlinear Ordinary Differential Equations [J]. Communin Nonlinear Sci Numer Simul,2010,15(10): 2778-2790.

[7] Yusufoglu E,Bekir A. Symbolic Computation and New Families of Exact Travelling Solutions for the Kawahara and Modified Kawahara Equations [J]. Comput &Math Appl,2008,55(8): 1113-1121.

[8] Aslan I. Exact and Explicit Solutions to Some Nonlinear Evolution Equations by Utilizing the (G′/G)-Expansion Method [J]. Appl Math Comput,2009,215(2): 857-863.

[9] Biswas A,Konar S,Zerrad E. Soliton Perturbation Theory for the General Modified Degasperis-Procesi Camasa-Holm Equation [J]. Inter J Mod Math,2007,2(1): 35-40.

[10] Bridges T J,Derks G. Linear Instability of Solitary Wave Solutions of the Kawahara Equation and Its Generalizations [J]. SIAM J Math Anal,2002,33(6): 1356-1378.

[11] Benjamin T B,Bona J L,Mahony J J. Model Equations for Long Waves in Nonlinear Dispersive Systems [J]. Philos Trans Roy Soc: Ser A,1972,272(1220): 47-48.