許友偉,姚靜蓀,劉燕

(安徽師范大學(xué)數(shù)學(xué)計算機科學(xué)學(xué)院,安徽蕪湖 241003)

一類具非線性邊界條件的高階方程的奇攝動問題

許友偉,姚靜蓀,劉燕

(安徽師范大學(xué)數(shù)學(xué)計算機科學(xué)學(xué)院,安徽蕪湖 241003)

通過引入伸展變量和非常規(guī)的漸近序列,運用合成展開法,對一類具非線性邊界條件的非線性高階微分方程的奇攝動問題構(gòu)造了形式漸近解,再運用微分不等式理論證明了原問題解的存在性及所得漸近近似式的一致有效性.

奇攝動;非線性邊界條件;高階微分方程;微分不等式理論

1 引言

近年來,對具非線性邊界條件的微分方程的奇攝動問題已有很多研究,如文獻[1-3]研究了具非線性邊界條件的二階微分方程的奇攝動問題,文獻[4-5]研究了具非線性邊界條件的三階微分方程的奇攝動問題,文獻[6]研究了具非線性邊界條件的四階微分方程的奇攝動問題,文獻[7]則研究了更為一般的具非線性邊界條件的n階微分方程的奇攝動問題.但文獻[7]中的假設(shè)[H4]要求P(λ0)=0,P′(λ0)/=0,即λ0為P(λ)=0的單根,該條件保證了用常規(guī)的漸近序列可以確定外部解,從而獲得復(fù)合解.本文摒棄關(guān)于單根的條件,討論在文獻[7]中已研究的如下奇攝動問題:

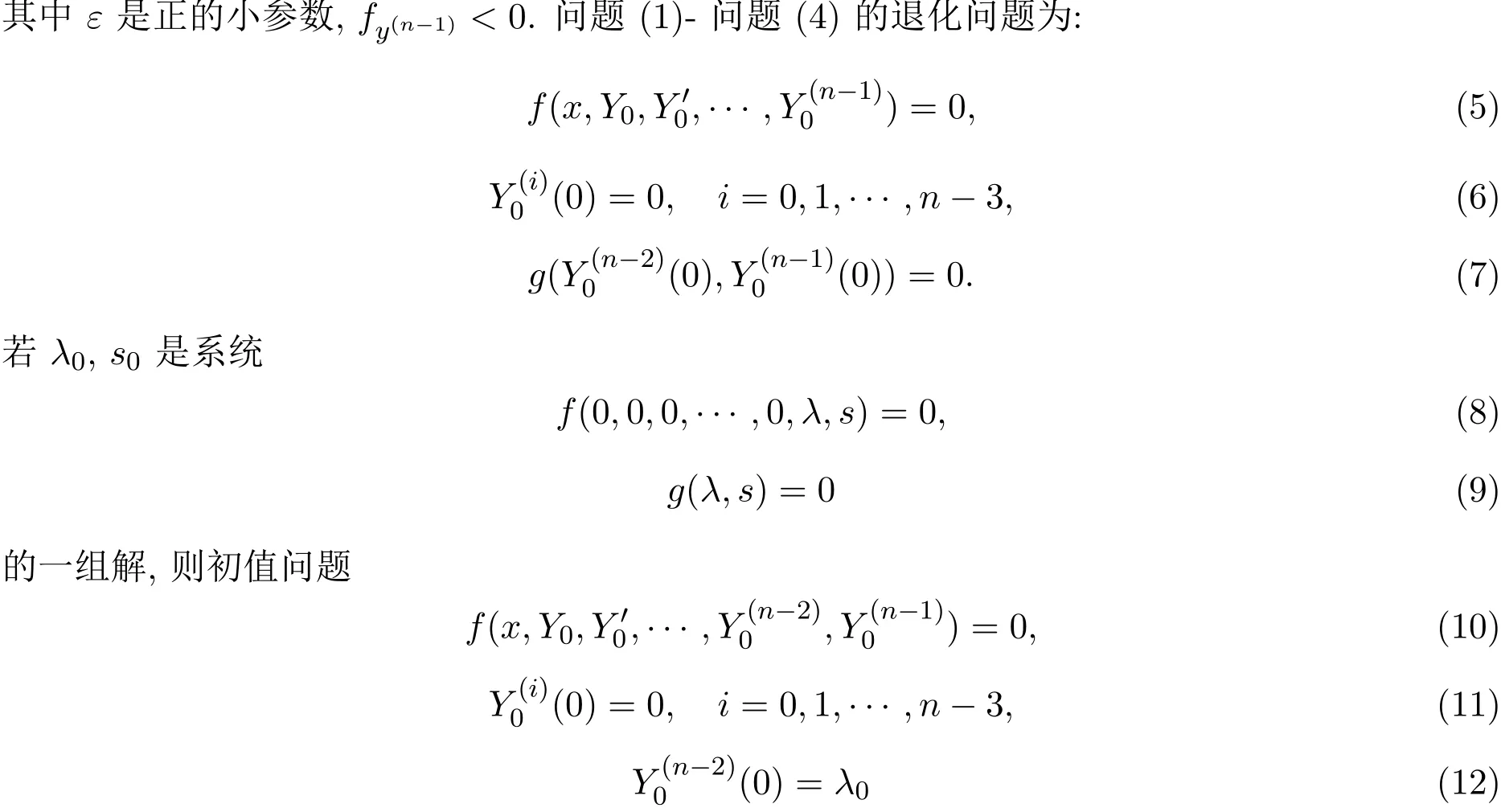
的解是退化問題(5)-問題(7)的解.

現(xiàn)作如下假設(shè):

[H1]函數(shù)f,g,h關(guān)于其變元在相應(yīng)的區(qū)域內(nèi)充分光滑,且對于各自變量的各階偏導(dǎo)有界,并存在正常數(shù)k0,δ0,使得

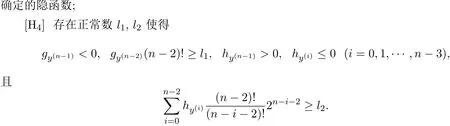
2 形式漸近解的構(gòu)造

3 主要結(jié)果

[1]莫嘉琪,韓祥臨.一類奇攝動非線性邊值問題[J].數(shù)學(xué)研究與評論,2002,22(4):626-630.

[2]Mo Jiaqi.The singularly perturbed nonlinear boundary value problems[J].Mathematica Applicata,2004, 17(1):37-41.

[3]吳欽寬.奇攝動積分微分方程非線性邊值問題[J].蘭州大學(xué)學(xué)報:自然科學(xué)版,2007,43(4):127-130.

[4]黃香蕉,明萬元.奇攝動三階非線性邊值問題[J].數(shù)學(xué)的實踐與認識,2011,41(8):177-181.

[5]吳有萍,姚靜蓀.一類具非線性邊值條件的非線性方程的奇攝動問題[J].應(yīng)用數(shù)學(xué)與計算數(shù)學(xué)學(xué)報, 2011,25(2):185-193.

[6]Li Xu,Wang Shipeng.Singular perturbations for a class of fourth-order nonlinear boundary value problem[J]. Chin.Quart.J.of Math.,2011,26(2):217-222.

[7]劉燕,姚靜蓀.一類高階方程的非線性邊界條件的奇攝動問題[J].高校應(yīng)用數(shù)學(xué)學(xué)報,2012,27(2):175-181.

[8]王立波,裴明鶴,葛渭高.一類n階非線性兩點邊值問題解的存在性與唯一性[J].應(yīng)用數(shù)學(xué)學(xué)報,2008,31(3):467-479.

A class of singular perturbed problems for higher order equations with nonlinear boundary value conditions

Xu Youwei,Yao Jingsun,Liu Yan
(College of Mathematics and Computer Science,Anhui Normal University,Wuhu241003,China)

The formal asymptotic solutions are constructed for a class of singular perturbed problems for higher order equations with nonlinear boundary value conditions by the introduction of the stretched variable and the unconventional asymptotic sequenceand the method of composite expansions.Then the existence of solutions for the original problems and the uniform validity of the asymptotic approximations are proved by the theory of differential inequality.

singular perturbation,nonlinear boundary value condition,higher order differential equation, the theory of differential inequality

O175.14

A

1008-5513(2013)02-0197-11

10.3969/j.issn.1008-5513.2013.02.014

2013-01-10.

國家自然科學(xué)基金(10901003);安徽高校省級自然科學(xué)基金(KJ2011A135).

許友偉(1989-),碩士生,研究方向:奇異攝動理論.

姚靜蓀(1956-),教授,研究方向:奇異攝動理論.

2010 MSC:34E20,34B15