張凌潔,蘇美紅,張海

(西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

LS,LAD組合損失的高維統(tǒng)計(jì)性質(zhì)分析

張凌潔,蘇美紅,張海

(西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

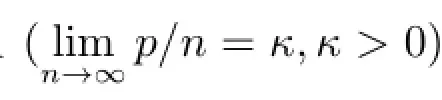
線性模型;高維;穩(wěn)健估計(jì);罰穩(wěn)健估計(jì);LS+LAD的凸組合

DO I：10.3969/j.issn.1008-5513.2013.05.014

1 引言

研究與應(yīng)用的階段,將穩(wěn)健統(tǒng)計(jì)數(shù)據(jù)擴(kuò)展到其他評(píng)估和測(cè)試的問題,同時(shí)建立穩(wěn)健估計(jì)的漸近理論,并講述有關(guān)穩(wěn)健性的相關(guān)知識(shí);文獻(xiàn)[6]對(duì)文獻(xiàn)[4]提出的案例(a)lim sup p＜∞做了分析;文獻(xiàn)[7]給出M估計(jì)中每個(gè)估計(jì)量的漸近有效性;文獻(xiàn)[8]介紹“一步法”的Huber(M)估計(jì)線性模型;文獻(xiàn)[9-11]給出?β的一致正態(tài)漸近分布;文獻(xiàn)[12]提出多參數(shù)線性模型M估計(jì)的漸近性和一致性;文獻(xiàn)[13-15]在一般損失函數(shù)下給出高維穩(wěn)健估計(jì)和高維罰穩(wěn)健估計(jì)求解‖?β‖(‖?β-β0‖)的方程組,并對(duì)如何適當(dāng)選擇損失函數(shù)的問題做以分析.

經(jīng)典地,通常研究p固定或p/n→0(觀測(cè)數(shù)n→∞比預(yù)測(cè)數(shù)p→∞的速度快)的情況,對(duì)于噪聲服從正態(tài)分布,最小二乘LS是優(yōu)的,而關(guān)于損失函數(shù)ρ是雙指數(shù)分布,最小絕對(duì)偏差LAD是優(yōu)的.

估計(jì)未知參數(shù)β時(shí),當(dāng)ε的分布是已知的(如正態(tài)的,均勻的,Weibull的等),通常采用最大似然估計(jì)法來估計(jì)未知參數(shù).若ε的分布是未知的,通常采用LS﹑M inMax(MM)和LAD等作估計(jì).如果誤差是正態(tài)分布,LS和最大似然估計(jì)是相同的,但是在響應(yīng)變量和解釋變量中, LS卻受離群值的影響.對(duì)響應(yīng)變量LAD是穩(wěn)健的,但LAD對(duì)于解缺乏唯一性.近幾年提出組合的方法是為了處理不確定性模型選擇的問題,該方法不僅節(jié)省了計(jì)算時(shí)間,提高了估計(jì)精度,而且在不確定性模型選擇時(shí),也給出了較好的估計(jì)量.比如組合的方法可以改善回歸的性能問題[16];用于穩(wěn)固和收縮系數(shù)估計(jì)的組合方法能提高預(yù)測(cè)[17];用回歸函數(shù)的參數(shù)和非參數(shù)的組合回歸估計(jì)時(shí),組合估計(jì)量?jī)?yōu)于核估計(jì)量[18].

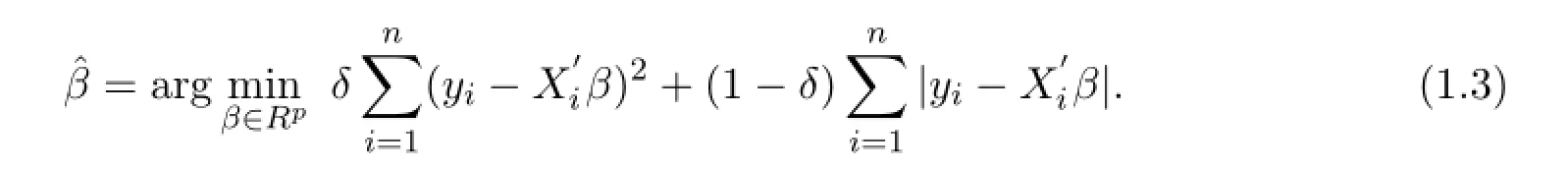
為了減弱LS受離群值的影響和LAD對(duì)解缺乏唯一性,用LS+LAD的凸組合形式[19-20],即其中0≤δ≤1.顯然,當(dāng)δ=0時(shí),模型為L(zhǎng)AD估計(jì),當(dāng)δ=1時(shí),模型為L(zhǎng)S估計(jì).適當(dāng)選擇δ是為了得到未知參數(shù)的最小漸近方差.組合模型允許組合一些已有模型來估算誤差,對(duì)已有模型的估計(jì)進(jìn)行改善,使其具有更多的性質(zhì):使不確定性模型的選擇有了依據(jù),節(jié)省了計(jì)算時(shí)間﹑提高了預(yù)測(cè)精度和估計(jì)的收斂率.特別,組合模型解決了解缺乏唯一性的問題.

然而,損失函數(shù)是LS+LAD凸組合形式的高維性質(zhì)還不清楚.本文主要是在高維背景(觀測(cè)數(shù)n和預(yù)測(cè)數(shù)p均趨于無窮大,即下,對(duì)LS+LAD的高維穩(wěn)健性質(zhì)(p＜n)和高維罰穩(wěn)健性質(zhì)(p?n)作以分析,性質(zhì)分析中主要運(yùn)用了prox函數(shù)和Stein′s identity[14],得到了穩(wěn)健估計(jì)和罰穩(wěn)健估計(jì)的顯示表達(dá),結(jié)果顯示這種凸組合損失函數(shù)模型集成了LS和LAD損失的優(yōu)點(diǎn),同時(shí)消弱了它們的不足,具有優(yōu)良的高維統(tǒng)計(jì)性質(zhì).

2 LS+LAD高維穩(wěn)健性質(zhì)分析(p＜n)

3 LS+LAD高維罰穩(wěn)健性質(zhì)分析(p?n)

4 結(jié)論

在高維穩(wěn)健回歸中,LS估計(jì)和LAD估計(jì)已有相對(duì)完善的理論結(jié)果,但是它們還存在一定的問題.LS在響應(yīng)變量和解釋變量中受離群值的影響;LAD在解釋變量中受離群值的影響,同時(shí)還對(duì)解缺乏唯一性.

本文主要針對(duì)損失函數(shù)為L(zhǎng)S+LAD的凸組合形式,研究了高維背景(觀測(cè)數(shù)n和預(yù)測(cè)數(shù)p均趨于無窮大,即

?運(yùn)用了prox函數(shù)和Stein′s identity,得到了凸組合損失下高維穩(wěn)健估計(jì)‖β‖和高維罰穩(wěn)健回歸估計(jì)‖β?-β0‖的顯示表達(dá),結(jié)果表明這種凸組合損失函數(shù)模型集成了LS和LAD損失的優(yōu)點(diǎn),同時(shí)消弱了它們的不足,具有優(yōu)良的高維統(tǒng)計(jì)性質(zhì).

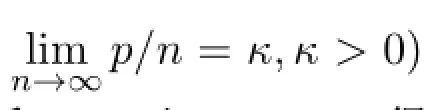
[1]陳希孺,趙林城.線性模型中的M方法[M].上海:上海科學(xué)出版社,1996.

[2]Huber P J.Robust estimation of a location parameter[J].Ann.Statist.,1964,35,73-101.

[3]Huber P J.The 1972Wald lecture.Robust statistics:A review[J].Ann.Statist.,1972,43:1041-1067.

[4]Huber P J.Robust regression:asym p totics,con jectures and M onte Carlo[J].Ann.Statist.,1973,1:799-821.

[5]Huber P J,Ronchetti E M.Robust Statistics[M].2nd ed.Hoboken,NJ:John W iley and Sons Inc,2009.

[6]Relles D.Robust Regression by M odifed Least Squares[C].New Haven:Ph.D.Thesis,Yale University,1968.

[7]Yohai V J.Robust Estimation in the Linear M odel[C].New Haven:Ph.D.Thesis,Yale University,1974.

[8]Bickel P J.One-step Huber estimates in the linearmodel[J].J.Amer.Statist.Assoc.,1975,70:428-434.

[9]Portnoy S.Asym p totic behavior of M-estim ators of p regression param eters w hen p2/n is large[J].Ann. Statist.,1984,12:1298-1309.

[10]Portnoy S.Asym p totic behavior of M estimators of p regression parameters when p2/n is large[J].Ann. Statist.,1985,13:1403-1417.

[11]Le Cam L.On the assum ptions used to prove asym ptotic norm ality of m aximum likelihood estim ates[J]. Ann.Statistics,1970,41:802-828.

[12]M ammen E.Asym ptotics w ith increasing dimension for robust regression w ith app lications to the bootstrap[J].Ann.Statist.,1989,17:382-400.

[13]Nou redd ine E l Karoui,Derek Bean,Peter B ickel,et al.On robust regression w ith high-d im ensional p red ictors[J].Proc.Natl.Acad.Sci.USA,2013,110(36):14557-14562.

[14]Derek Bean,Peter Bickel,Noureddine El Karoui,et al.Penalized Robust Regression in High-Dimension[C]. Berkeley:Technical Reports of Departm en t of Statistics University of California,2011.

[15]Derek Bean,Peter Bickel,Noureddine El Karoui,et al.Op timal Ob jective Function in High-Dimensional regression[C].Berkeley:Technical Reports of Department of Statistics University of California,2011.

[16]Sculley D.Combined regression and ranking[J].Washington,DC,USA,K.D.D.,2010,10:25-28.

[17]W ei X iaoqiao.regression-based forecast com bination m ethods[J].Rom anian Jou rnal for Econom ic Forecasting,2009(4):5-18.

[18]Fan Yanqin.Asym p totic Normality of a combined regression estimator[J].Journal ofM u ltivariate Analysis, 1999,71:191-240.

[19]Enrique Castillo,Carm en Castillo,A li S Had i,et al.Combined regression m od les[J].Com pu t.Stat., 2009,24:37-66.

[20]Rosasco E,De V ito A,Caponnetto M,et al.Are loss functions all the same?[J].Neural.Com put., 2003,16(5):1063-1076.

[21]Akaike H.In formation Theory and an Extension of the Mmaximum Likelihood Princip le[D].Budapest: Akadem iai K iado,1973.

[22]Schwarz G.Estimating the dimension of amodel[J].Ann Stat.,1978,6:461-464.

[23]Xu Zongben,Zhang Hai,W ang Yao,et al.L1/2Regu larization[J].Sci.China In f.Sci.,2010,53:1159-1169.

[24]Zhang Hai,Liang Yong,Gou HaiLiang,et al.The essential ability of sparse reconstruction of dif erent com p ressive sensing strategies[J].Sci.China In f.Sci.,2012,55:2582-2589.

[25]Xu Zongben,Chang X iangyu,Xu Fengm in,et al.L1/2Regu larization:a th reshold ing rep resentation theory and a fast solver[J].Neu ral Networks and Learning System s.2012,23(7):1013-1027.

[26]Tibshirani R.Regression shrinkage and selection via the Lasso[J].Journal of the Royal Statistical Society Series,1996,58(1):267-288.

[27]M allow s C L.Som e comm ents on Cp[J].Technom etrics,1973,15:661-675.

[28]Peter Buhlmann Sara van de Geer.Statistics for High-Dimensional Data[M].New York:Springer,2010.

[29]Fan JQ,LiR Z.Variab le selection via nonconcave penalized likelihood and its oracle p roperties[J].Journal of the American Statistical Association,2001,31:1348-1360.

The statistical analysis of the com bined loss of
LS,LAD in h igh-d im ension

Zhang Lingjie,Su Meihong,Zhang Hai

(Department of Mathematics,Northwest University,X i′an 710127,China)

This article studies a convex combination of the Least Squares(LS)and Least Absolute Deviation(LAD).By studying the robust statistical properties of high-dimensional and penalized robust statistical p roperties of high d im ension when the number of observations n and the num ber of p rediction p tends to inf nitythe exp ressions of robust estim ation and penalized robust estim ation are obtained.The

result reveals that the loss function model of convex combination combines the advantages of the LSand LAD, at the same time,it relatively weakens their shortcom ings,thus it has excellent high dimensional statistical p roperties.

linearmodel,high dimension,robust estimation,penalized robust estimation, convex combination of LS+LAD

O23

A

1008-5513(2013)05-0536-08

2013-05-16.

國(guó)家自然科學(xué)基金(11171272).

張凌潔(1986-),碩士生,研究方向:機(jī)器學(xué)習(xí).

2010 MSC:94A 15