楊曉亞

(天水師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 天水 741001)

圖Pn□Cm的鄰點(diǎn)可區(qū)別I-全染色

楊曉亞

(天水師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 天水 741001)

通過(guò)對(duì)圖Pn□Cm的積圖的鄰點(diǎn)可區(qū)別全染色研究,來(lái)進(jìn)一步驗(yàn)證鄰點(diǎn)可區(qū)別全染色的猜想.應(yīng)用構(gòu)造具體染色的方法給出了圖Pn□Cm的積圖的鄰點(diǎn)可區(qū)別全染色.得到了圖Pn□Cm的積圖的鄰點(diǎn)可區(qū)別全染色的色數(shù).

I-全染色;鄰點(diǎn)可區(qū)別I-全染色;鄰點(diǎn)可區(qū)別I-全色數(shù)

1 引言

圖的染色是圖論的重要研究?jī)?nèi)容之一,由計(jì)算機(jī)科學(xué)和信息科學(xué)等所產(chǎn)生的點(diǎn)可區(qū)別邊染色[1-9],鄰點(diǎn)可區(qū)別邊染色(或鄰強(qiáng)邊染色)[24]及鄰點(diǎn)可區(qū)別全染色[5-6]等都是十分困難的問(wèn)題,至今文獻(xiàn)甚少.在此基礎(chǔ)之上,張忠輔等人進(jìn)一步提出了圖的新染色概念,圖的鄰點(diǎn)可區(qū)別I-全染色是其中之一[7].本文給出了路Pm和圈Cn的Cartesian積圖的鄰點(diǎn)可區(qū)別I-全色數(shù).

定義1.1[6]設(shè)G是階至少為2的連通圖,k為正整數(shù),f是圖G的使用顏色為1,2,···,k的正常全染色.?x∈V(G),令C(x)表示在f下點(diǎn)x的顏色及與x關(guān)聯(lián)的全體邊的顏色構(gòu)成的集合,稱(chēng)之為在全染色f下點(diǎn)x的色集合.如果?uv∈E(G),有C(u)?=C(v),則f稱(chēng)為G的k-鄰點(diǎn)可區(qū)別全染色.稱(chēng)

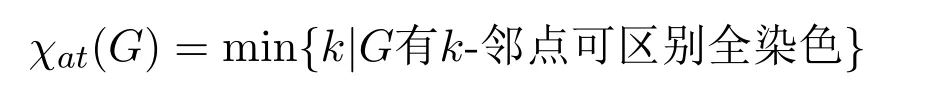
為G的鄰點(diǎn)可區(qū)別全色數(shù).

定義1.2[7]設(shè)G是階至少為2的連通圖,k為正整數(shù),f是圖G的使用顏色為1,2,···,k的全染色.如果G的任意相鄰的點(diǎn)染不同的顏色,并且G的任意相鄰的邊染不同的顏色,那么稱(chēng)f為G的I-全染色.設(shè)f是G的I-全染色,?x∈V(G),令C(x)表示在f下點(diǎn)x的顏色及與x關(guān)聯(lián)的全體邊的顏色構(gòu)成的集合,稱(chēng)之為在f下點(diǎn)x的色集合.如果?uv∈E(G),有C(u)?=C(v),則f稱(chēng)為G的k-鄰點(diǎn)可區(qū)別I-全染色(簡(jiǎn)記為k-AVDIT染色).稱(chēng)

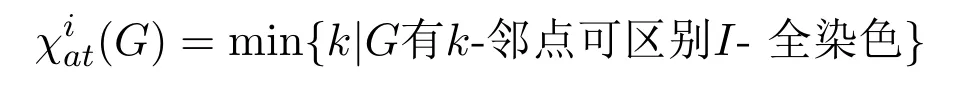
2 主要結(jié)果

[1]Favaron O,Li H,Schelp R H.Strong edge colorings of graphs[J].Discrete Mathematica,1996,159:103-109.

[2]Zhang Zhongfu,Liu Linzhong,Wang Jianfang.Ad jacent strong edge coloring of graphs[J].App lied M athematica Letters,2002,15:623-626.

[3]Li Jingwen,Zhang Zhongfu,Chen X iang′en,et al.A note on ad jacent strong edge coloring of K(n,m)[J]. Acta M athem aticae App licatae Sinica(English Series),2006,22(2):273-276.

[4]Zhang Zhongfu,Li M uchun,Yao Bing,et al.On the vertex distinguishing equitable edge-colouring of graphs[J].A rs Combinatoria,2008,86:193-200.

[5]陳祥恩.關(guān)于圖rK2∨Ks的鄰點(diǎn)可區(qū)別全色數(shù)[J].蘭州大學(xué)學(xué)報(bào),2007,43(5):91-93.

[6]陳祥恩,張忠輔.關(guān)于圖K2n+1?E(2K2)的鄰點(diǎn)可區(qū)別全色數(shù)[J].蘭州大學(xué)學(xué)報(bào),2005,41(6):102-105.

[7]Zhang Zhongfu,WoodallD R,Yao Bing,et al.Ad jacent vertex-distinguishing I-totalcoloring ofgraphs[EB/OL]. (2008-06-12)[2008-07-24]http://202.201.18.40:8080/m as5/.

[8]Bondy J A,Murty U SR.Graph Theory[M].London:Springer,2008.

[9]王治文,文飛,楊隨義,等.圖K2nE(F5)(n≥13)的點(diǎn)可區(qū)別邊染色[J].河南師范大學(xué)學(xué)報(bào),2010,38(6):1-3.

Adjacent vertex-d istinguish ing I-total colorings of Pn□Cm

Yang Xiaoya

(Departm ent of M athem atics,T ianshui Norm al University,T ianshui 741001,China)

The con jecture on ad jacent vertex-distinguishing I-total colorings of graphs is proved through adjacent vertex-distinguishing I-total colorings of Pn□Cm.The ad jacent vertex-distinguishing I-total colorings of Pn□ Cmis given by m ethod of constructing concrete coloring.The ad jacent vertex-distinguishing I-total chrom atic numbers of Pn□Cmis obtained.

I-total coloring,ad jacent vertex-distinguishing I-total coloring, ad jacent vertex-distinguishing I-total chromatic number

O157.5

A

1008-5513(2012)06-0757-08

2012-06-15.

甘肅省自然科學(xué)基金(096RJZE106);天水師范學(xué)院中青年教師科研資助項(xiàng)目(TSA 1102).

楊曉亞(1977-),碩士,講師,研究方向:計(jì)算機(jī)網(wǎng)絡(luò)控制與圖的染色.

2010 M SC:05C15