鞠培軍,田力,孔憲明,張衛(wèi),劉國彩

(泰山學院數(shù)學與系統(tǒng)科學學院,山東 泰安 271021)

統(tǒng)一混沌系統(tǒng)的全局指數(shù)吸引集的新結(jié)果

鞠培軍,田力,孔憲明,張衛(wèi),劉國彩

(泰山學院數(shù)學與系統(tǒng)科學學院,山東 泰安 271021)

研究了參數(shù)α∈[1/29,14/173)時,統(tǒng)一混沌系統(tǒng)的全局指數(shù)吸引集問題.通過線性變換和廣義Lyapunov函數(shù)方法,給出了系統(tǒng)最終上界的精確估計.所得結(jié)果發(fā)展和豐富了現(xiàn)有混沌系統(tǒng)吸引集的結(jié)果,并將在混沌控制和同步中得到廣泛應用.

統(tǒng)一混沌系統(tǒng);全局指數(shù)吸引集;廣義Lypunov函數(shù)

1 引言

自從20世紀60年代Lorenz在氣象數(shù)值研究中偶爾發(fā)現(xiàn)了第一個混沌吸引子以來[1],混沌已在許多領域中獲得了巨大而深遠的發(fā)展[25].特別是最近十多年來,混沌控制和同步得到廣泛而深入的研究[25],其中許多結(jié)論的證明都用到了混沌系統(tǒng)最終有界的假設,因此對混沌系統(tǒng)最終有界性的研究顯得非常重要.但由于混沌系統(tǒng)的方程組是非線性的,進行純理論分析較困難.直到2002年,一些作者才首次從數(shù)學理論的高度嚴格論證了Lorenz吸引子存在性的信息[67].文獻[8]針對Lorenz系統(tǒng),得到系統(tǒng)全局吸引集的一個圓柱形估計式和一個球形估計式.隨后,針對Lorenz系統(tǒng),在不同的條件下,又有一些新的結(jié)果出現(xiàn)[913].

文獻[2]提出了一類統(tǒng)一混沌系統(tǒng):

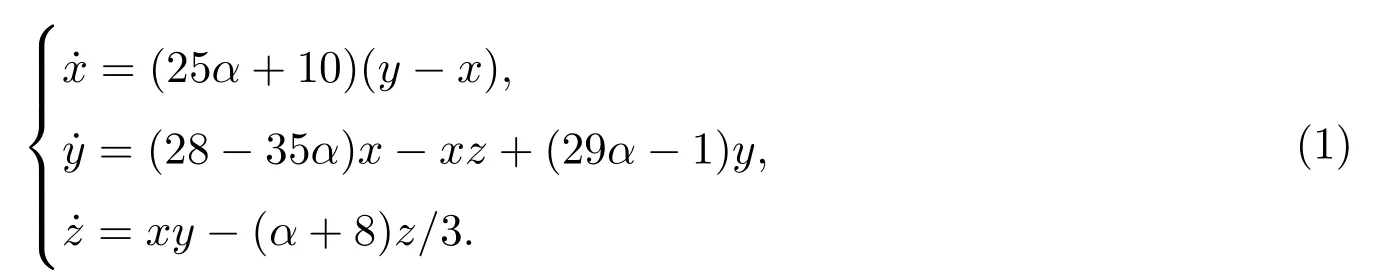
當 α∈[0,1]時,系統(tǒng) (1)具有混沌吸引子.文獻 [9-10]利用 Lagrange極值理論和廣義 Lyapunov函數(shù),給出了統(tǒng)一混沌系統(tǒng)的全局吸引集和正向不變集的估計結(jié)果.最近,文獻[11-13]通過構造廣義正定徑向無界Lyapunov函數(shù),給出了Lorenz系統(tǒng)全局指數(shù)吸引集的統(tǒng)一結(jié)果,囊括了目前一些類似結(jié)果為特例.但是以上結(jié)果都是基于α∈[0,1/29)的前提,對于在其他范圍時相應混沌系統(tǒng)的全局吸引集問題還少有人研究.本文將考慮α∈[1/29,14/173)時,統(tǒng)一混沌系統(tǒng)(1)的全局指數(shù)吸引集問題.

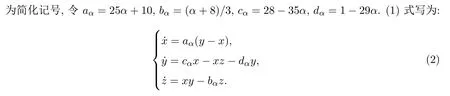
由于α∈[1/29,14/173)時,系統(tǒng)(2)的線性部分系數(shù)矩陣的主對角元參數(shù)含有-dα≥0,文獻[12-13]的方法(僅適合主對角元都為負數(shù)的情況),在此已不再適合,需要考慮新的方法.本文將先給出一些引理,再通過線性變換和廣義Lyapunov函數(shù)方法,給出系統(tǒng)(2)吸引集的指數(shù)估計式.

2 全局指數(shù)吸引集

3 結(jié)論

針對參數(shù)α∈[1/29,14/173)時,統(tǒng)一混沌系統(tǒng)的線性部分系數(shù)矩陣的主對角元中含有非負參數(shù)的情況,本文利用廣義Lyapunov函數(shù)方法研究了其全局指數(shù)吸引集問題,給出了系統(tǒng)吸引集的精確估計,推廣了現(xiàn)有結(jié)果.所得結(jié)果可直接應用到混沌控制和同步中.

附錄

[1]Lorenz E N.Deterministic non-periodic fl ow[J].J.Atoms.Sci.,1963,20(3):130-141.

[2]陳關榮,呂金虎.Lorenz系統(tǒng)族的動力學分析、控制與同步[M].北京:科學出版社,2003.

[3]王興元.復雜非線性系統(tǒng)的混沌[M].北京:電子工業(yè)出版社,2003.

[4]關新平,范正平,陳彩蓮,等.混沌控制及其在保密通信中的應用[M].北京:國防工業(yè)出版社,2002.

[5]楊萬利,王鐵寧.非線性動力學理論及應用[M].北京:國防工業(yè)出版社,2007.

[6]Tucker W.A rigorous ODE solver and Smale′s 14 problem[J].Found.Comput.Math.,2002,2:53-117.

[7]Stwart I.The Lorenz attractor exists[J].Nature,2002,406:9498-949.

[8]Leonov G A.Bound for attractors and the existence of Hornoclinic orbits in the Lorenz system[J].J.Appl. Math.Mech.,2001,65(1):19-32.

[9]Li D,Lu J,Wu X,et al.Estimating the bounds for the Lorenz family of chaotic system[J].Chaos,Solitons and Fractals,2005,23:529-534. [10]Li D,Lu J,Wu X,et al.Estimating the ultimate bound and positive invariant set for the Lorenz system and a uni fi ed chaotic system[J].Journal of Mathematical Analysis Application,2006,323:844-653.

[11]廖曉昕.論Lorenz混沌系統(tǒng)全局吸引集和正向不變集的新結(jié)果即對混沌控制與同步的應用[J].中國科學:E輯,2004,34(12):1404-1419.

[12]廖曉昕,羅海庚,傅予力,等.論 Lorenz系統(tǒng)族的全局指數(shù)吸引集和正向不變集 [J].中國科學:E輯, 2007,37(6):757-769.

[13]Liao X X,Fu Y,Xie S,et al.Globally exponentially attractive sets of family if Lorenz systems[J].Science in China(Ser.F),Information Sciences,2008,51:283-292.

New results of globally exponentially attractive set of
a uni fi ed chaotic system

Ju Peijun,Tian Li,Kong Xianming,Zhang Wei,Liu Guocai
(Department of Mathematics and System Science,Taishan University,Taian 271021,China)

The globally exponentially attractive set of a uni fi ed chaotic system with the parameter α∈[1/29,14/173)was discussed by using linear reformation and the generalized Lyapunov function,and the explicit estimations of the ultimate bound is derived.The established theorems in this paper develop and extend the existing achievements on attractive set of chaotic system.The obtained results will fi nd wide application in chaos control and synchronization.

uni fi ed chaotic system,globally exponentially attractive set,generalized Lyapunov function

O29;O415.5

A

1008-5513(2012)01-0113-06

2011-06-10.

山東省軟科學研究計劃項目(2010RKGA2051).

鞠培軍(1975-),碩士,研究方向:混沌系統(tǒng),時滯系統(tǒng).

2010 MSC:03C65