謝樂平, 吳毅清

(懷化學(xué)院數(shù)學(xué)系,湖南懷化 418008)

形式三角矩陣環(huán)的雙導(dǎo)子

謝樂平, 吳毅清

(懷化學(xué)院數(shù)學(xué)系,湖南懷化 418008)

設(shè)A,B是有單位元的環(huán),M為(A,B)-雙模,研究形式三角矩陣環(huán)Tri(A,M,B)的雙導(dǎo)子,利用代數(shù)方法得到了形式三角矩陣環(huán)Tri(A,M,B)的雙導(dǎo)子的具體結(jié)構(gòu)形式.

形式三角矩陣環(huán); 雙導(dǎo)子

假定A,B是兩個有單位元的環(huán),一個(A,B)-雙模M是指M是一個左A-模,也是一個右B-模,并且/a∈A,m∈M,b∈B,有(am)b=a(mb).形式三角矩陣環(huán)定義為

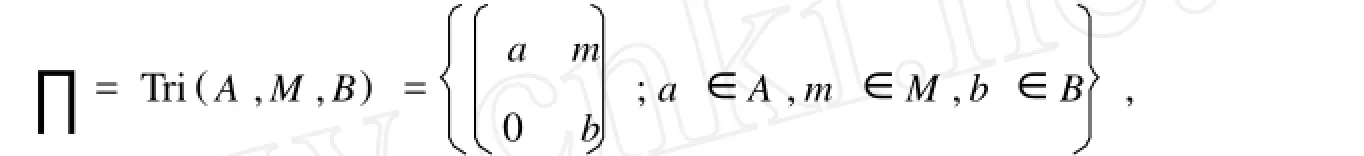
其加法和乘法按通常矩陣的運算進行.人們對這種形式三角環(huán)(也是三角代數(shù))進行了許多研究.如[1]對形式三角矩陣環(huán)的各種性質(zhì)做了系統(tǒng)的研究,[2]研究了三角代數(shù)的交換映射,即使[L(a),a]=0的線性映射L,這里a是三角代數(shù)的任一元素.[3]給出了三角代數(shù)的Lie導(dǎo)子的結(jié)構(gòu).[4]研究了三角代數(shù)上雙可加映射的交換跡和Lie同構(gòu).[5]描述了三角代數(shù)的Jordan同構(gòu).[6]探討了三角代數(shù)的Jordan導(dǎo)子.[7]給出了三角矩陣環(huán)的導(dǎo)子和自同構(gòu)的結(jié)構(gòu)形式.所以研究這種三角矩陣環(huán)是有意義的工作.大家都知道:探討一個代數(shù)結(jié)構(gòu)的導(dǎo)子也是有意義的,主要是研究導(dǎo)子的性質(zhì)、結(jié)構(gòu)形式和應(yīng)用.雙導(dǎo)子由于對每一個分量都是導(dǎo)子,所以比導(dǎo)子更加復(fù)雜,[8]證明了非交換素環(huán)上的雙導(dǎo)子都是內(nèi)雙導(dǎo)子.[9]給出了雙導(dǎo)子在某些域上的應(yīng)用.本文的目的是確定形式三角矩陣環(huán)Tri(A,M,B)的雙導(dǎo)子的具體結(jié)構(gòu)形式.

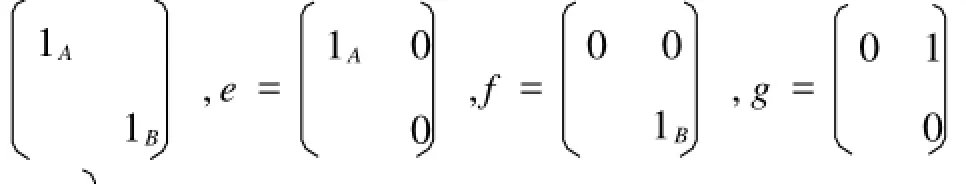
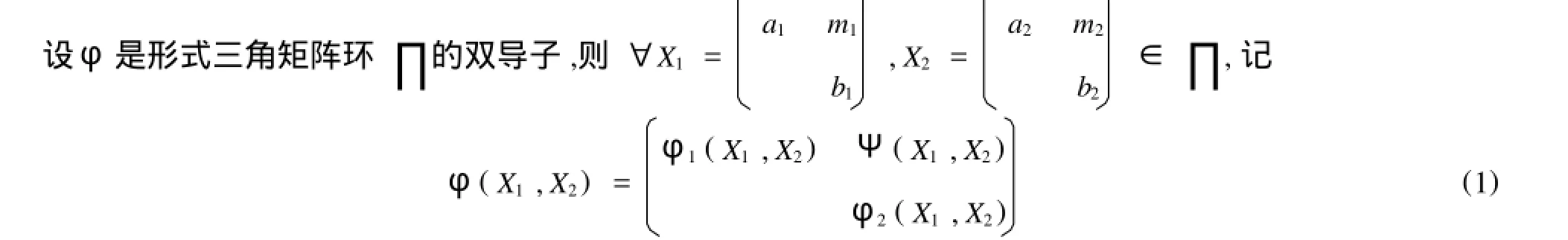
從定理2可以看出:形式三角矩陣環(huán)上的雙導(dǎo)子完全由M中的元素s=IM(eφ(e,e)f),t=IM(eφ(g,g)f)決定,但注意s,t可以取M中任意的元素.

[1]A.haghany and K.Varajan,Study of formal triangular matrix rings[J].Comm.Algebra.1999,27(11):5507-5525.

[2]W.S.Cheung,Commuting maps of triangular algebras[J].J.London Math.Soc.2001,63(2):117-127.

[3]W.S.Cheung,Lie derivations of triangular of triangular algebras[J].Linear Multilinear Algebra.2003,51:299-310.

[4]D.Benkovic,D.Eremita,Commuting traces and commutativety preserving maps on triangular algebras[J].J.Algebra.2004,280: 797-824.

[5]T.L.Wong,Jordan isomorphisms of triangular rings[J].Proc.Amer.Math.Soc.2005,133:3381-3388.

[6]J.H.Zhang,W.Y-yua,Jordan derivations of triangular algebras[J].Linear Algebra Appl.2006,419:251-255.

[7]謝樂平,曹佑安.形式三角矩陣環(huán)的導(dǎo)子和自同構(gòu)[J].數(shù)學(xué)雜志,2006,26(2):165-170.

[8]M.Bresar,W.S.Martindale,C.R.Miers,Centralizing maps in prime rings with involution[J].J.Algebra.1993,161:342-357.

[9]M.Bresar,Commuting maps:A survey[J].Taiwanese J.Math.2004,(8):361-397.

Abstract:This paper researches biderivations of the formal triangular matrix ring Tri(A,M,B)and obtains the structure form of the biderivation by using algebraic method.

Key words:formal triangular matrix ring; biderivation

Biderivations of Formal Triangular Matrix Rings

XIELe-ping, WU Y i-qing

(Dept of Math.,Huaihua University,Huaihua,Hunan 418008)

O151.21

A

1671-9743(2011)02-0019-04

2010-12-03

湖南省教育廳資助科研項目(04C470);懷化學(xué)院青年基金項目(HHUQ2009-04)1

謝樂平(1976-),男,湖南寧鄉(xiāng)人,懷化學(xué)院講師,碩士,主要研究結(jié)合代數(shù)1