WANG Xiao-ping,GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

The Derivation A lgebra of the Schrdinger-Viraso ro Lie A lgebra*

WANG Xiao-ping,GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

Fo r the perfect Lie algebra w ith one-dimensional center at lest,there is not a general result about the relationship between its derivation algebra and that of its universal central extension.In this paper,we determine the derivation algebra of the Schr?dinger-Viraso ro Lie algebra L,w hich is the universal central extension of the Schrdinger-Virasoro Lie algebraw ith one-dimensional center.It is p roved that L has only one outer derivation,w hilehas three outer derivations[1].Hence,we get one examp le that the derivation algebra of the universal central extension of a Lie algebra,the center of w hich is not zero,is not isomorphism to that of the Lie algebra.

Schrdinger-Virasoro algebra;central extension;derivation

MSC 2000:17B40

0 In troduction

The Schr?dinger-Viraso ro Lie algebra,o riginally introduced by M.Henkel in[2]during his study on the invariance of the free Schr?dinger equation,is a vecto r space over the comp lex field C w ith a basisand the Lie brackets:

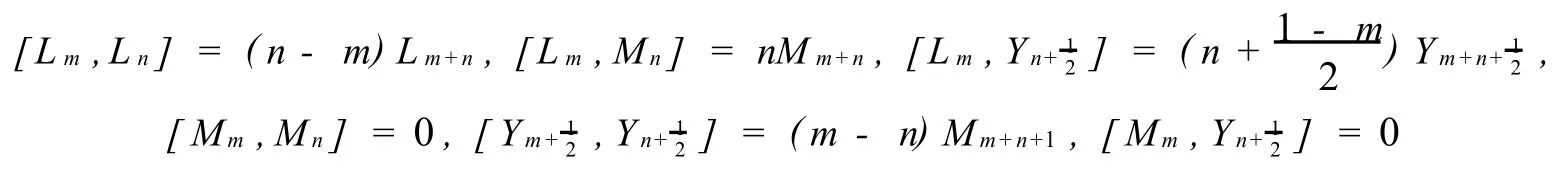
for all m,n∈Z.Due to its important app lications in many areas of Mathematics and Physics,the structure and rep resentation theory ofhave been extensively studied.For examp le,M.Henkel investigated thathasone-dimensional universal central extension in[2].C.Roger and J.Unterberger p resented a detailed cohomological study and determinedhas three outer derivations[1].And the automorphism group ofis determined in[3].Nowadays,extensions and generalizations related to the Schr?dinger-Virasoro algebra have appeared and their structure and rep resentation theory have been extensively studied,such as[4]～[6].

The derivation algebra of a centerless perfect Lie algebra is isomorphism to that of the universal central extension of the Lie algebra[7].While for the perfect Lie algebra w ith one-dimensional center at lest,there is not a general result about the relationship between its derivation algebra and that of its universal central extension.In this paper,we determine the derivation algebra of the Schr?dinger-Virasoro Lie algebra L,w hich is the universal central extension of the Schr?dinger-Virasoro Lie algebraw ithone-dimensional center.It show s that L has only one outer derivation,w hilehas three outer derivation[1].Therefo re,the derivation algebra of L is not isomo rphism to that of.

Throughout the paper,we denote by Z and C*the set of integers and the set of non-zero comp lex numbers respectively,and all the vector spaces are assumed over the comp lex field C.

1 The Derivation Algebra of L

[1]ROGER C,UN TERBERGER J.The Schrdinger-Viraso ro Lie group and algebra:Rep resentation theo ry and cohomological study[J].Annales Henri Poincar,2006(7～8):1477～1529.

[2]HENKEL M.Schrodinger invariance and strongly anisotropic critical systems[J].J Stat Phys,1994,75:1023～1061.

[3]GAO S.The automorphism group of the Schr?dinger-Virasoro Lie algebra[J].Journal of Huzhou Teachers College,2010,32:1:6～10.

[4]GAO S,JIANG C,PEI Y.Structure of the extended Schr?dinger-Viraso ro Lie algebra[J].A lgebra Colloq,2009,16:4 549～566.

[5]L IJ,SU Y.Rep resentations of the Schrodinger-Viraso ro algebras[J].J Math Phys,2008,49,053512:14.

[6]UNTERBERGER J.On vertex algebra rep resentations of the Schr?dinger-Viraso ro Lie algebra[EB/OL].[2007-03-21].arXiv:cond-mat/0703214v2.

[7]BEN KART G,MOODY R.Derivations,central extensions and affine Lie algebras[J].A lgebras Groups Geom,1986,3(4):456～492.

[8]FARNSTEINER R.Derivations and extensions of finitely generated graded Lie algebras[J].J Algebra,1988,118(1):34～45.

MSC 2000:17B40

王曉萍,高壽蘭

(湖州師范學院理學院,浙江湖州313000)

對于中心非零的perfect李代數,關于它的泛中心擴張的導子代數與它本身的導子代數之間的關系尚未有一個一般的結論.通過計算帶有一維中心的 Schr?dinger-Virasoro李代數的泛中心擴張L的導子,證明了L只有一個外導子,而由文獻[1]知有三個外導子,從而得到了一個中心非零的perfect李代數的導子代數與其泛中心擴張的導子代數不同構的例子.

Schrodinger-V iraso ro李代數;中心擴張;導子

O152.5

O152.5 Document code:A Article ID:1009-1734(2010)02-0022-05

date:2010-01-21

Biography:WANG Xiao-ping,Undergraduate student of grade 2006,Faculty of Science,Huzhou Teachers College,

Research Interests:Lie algebra.