任國花,高玉斌

一類譜任意符號模式

任國花,高玉斌

(中北大學數(shù)學系,山西太原030051)

運用Nilpotent-Jacobian方法證明了一類有2n+1個非零元的n階(n≥6)符號模式是譜任意模式.

符號模式矩陣;冪零矩陣;譜任意;極小譜任意

0 引言

元素取自集合{+,-,0}的矩陣為符號模式矩陣,簡稱為符號模式.若A=[aij]是一個實矩陣,則把由aij的符號為元素所組成的矩陣稱為A的符號模式,記為sgnA.對一個n階符號模式A,A的定性矩陣類定義為

對兩個同階符號模式A=[aij]和～A=[～aij],如果當aij≠0時,～aij=aij,則稱～A為A的母模式,A為～A的子模式.顯然,符號模式A既是它本身的母模式又是它的子模式.我們稱符號模式A的不是它本身的子模式為A的真子模式.對n階符號模式A,如果存在一個實矩陣B∈Q(A)使B的特征多項式fB(x)=xn,則稱A蘊含冪零,B為冪零矩陣.如果對任意n次首1實系數(shù)多項式r(x),在符號模式A的定性矩陣類Q(A)中存在一個矩陣B,使得B的特征多項式fB(x)=r(x),則稱A是譜任意的.顯然,如果A是譜任意的,那么它一定蘊含冪零.如果譜任意模式A的任意一個真子模式都不是譜任意的,則稱A為極小譜任意的.對一個n階符號模式A,若任一矩陣B∈Q(A)是非奇異的,則A是符號非奇異的;若每一個矩陣B∈Q(A)是奇異的,則A是符號奇異的.

譜任意符號模式的概念最早由文[1]提出,并據(jù)隱函數(shù)存在定理給出了一種證明符號模式是譜任意的Nilpotent-Jacobian方法(下節(jié)引理1.1),其后文[2-5]等分別給出了一些n階的譜任意模式.本文證明了一類有2n+1個非零元的n階(n≥6)符號模式是譜任意模式,并研究了它的極小性.

1 預備知識

本文研究如下類型的n階(n≥6)符號模式

引理1.1[1]A是一個n階符號模式,若B∈Q(A)為冪零矩陣,且B中至少含有n個非零元ai1j1,ai2j2,…,ainjn.把B中的這n個非零元用變量x1,…,xn代替后所得的矩陣記為X,且記X的特征多項式為pX(x)

其中βi∈{+,-},i=1,2,…,n+1.

設B∈Q(A),由于相似矩陣有相同的特征多項式,不妨設B有如下形式:

其中sgn(ai)=βi,i=1,2,…,n+1.

引理1.2 設B∈Q(A)有形式(2),其特征多項式為fB(x)=xn+α1xn-1+α2xn-2+…+αn-1x+αn,則: 1)

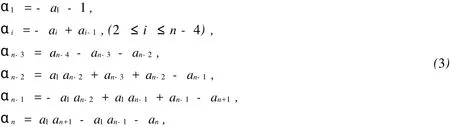
2)

證明:(1)

將第i行的x倍加到第i+1行(i=1,2,…,n-3),并依次按第三列展開,得:

因此1)成立.

2)對任意給定的an-1,

引理得證.

下面給出四種具有形式(1)的符號模式A1,A2,A3和A4,其中

(1)βi=-,(i=1,2,…,n-4),βn-3=βn-1=+,βn-2=βn+1=-,βn=+,記為A1.

(2)βi=-,(i=1,2,…,n-4),βn-3=βn-1=-,βn-2=βn+1=-,βn=+,記為A2.

(3)βi=-,(i=1,2,…,n-4),βn-3=βn-1=-,βn-2=βn+1=-,βn=-,記為A3.

(4)βi=-,(i=1,2,…,n-4),βn-3=βn-1=-,βn-2=βn+1=+,βn=-,記為A4.

引理1.3 符號模式A蘊含冪零當且僅當A是A1,A2,A3,A4其中之一.

證明 必要性.設符號模式A蘊含冪零,則存在實矩陣B∈Q(A)是冪零的.不妨設B形如(2),此時引理1.1中,α1=α2=…=αn=0.因為有n個方程n+1個未知數(shù),所以可以用an-1表示出其他的n個變量.從而得:ai=-1<0(i=1,2,…,n-4)

由an-1的取值范圍(an-1>0,-1/2

充分性.設實矩陣B∈Q(A)有形式(2).

若(a1,a2,…,an-4,an-3,an-2,an,an+1)=(-1,-1,…,-1,2,-3,5,-3),則實矩陣B∈Q(A1)是冪零的.

若(a1,a2,…,an-4,an-3,an-2,an,an+1)=(-1,-1,…,-1,-1/4,-3/4,1/2,-3/4),則實矩陣B∈Q (A2)是冪零的.

若(a1,a2,…,an-4,an-3,an-2,an,an+1)=(-1,-1,…,-1,-3/4,-1/4,-1/2,-1/4),則實矩陣B∈Q(A3)是冪零的.

若(a1,a2,…,an-4,an-3,an-2,an,an+1)=(-1,-1,…,-1,-2,1,-3,1),則實矩陣B∈Q(A4)是冪零的.引理得證.

2 主要結(jié)果

定理2.1 若n階(n≥6)符號模式A具有形式(1),則A是譜任意的當且僅當A是A1,A2,A3,A4其中之一,且A1,A2,A3,A4的每一個母模式都是譜任意的.

證明:由引理1.3知當且僅當A是A1,A2,A3,A4其中之一時,A蘊含冪零,結(jié)合引理1.1和1.3的2),定理得證.

定理2.2 符號模式A1是極小譜任意的.

證明:設T=[tij]是符號模式A1的一個子模式,且T是譜任意的,則:

(1)t1,1≠0且tn,n≠0,否則T的跡恒為正或負.

(2)ti,i+1≠0,i=1,2,…,n-1,否則T是一個2×2的下三角分塊矩陣,且T的對角線上的分塊矩陣的跡都非零,與“T是譜任意的”矛盾.

(3)tn-1,2≠0,否則T是符號非奇異的.

(4)ti,1≠0,i=2,…,n-4,否則αi≠0.

(5)tn-3,1≠0,否則tn-1,2=0與(3)矛盾.

(6a)tn-2,2≠0,否則αn-3<0.

(6b)tn,2≠0,否則與(6a)矛盾.

(6c)tn,1≠0,否則得αn=a1an+1-a1an-1=a1(an+1-an-1)>0.

所以A1的任意真子模式都不是譜任意的.定理得證.

類似地,可以證明以下定理.

定理2.3 符號模式A4是極小譜任意的.

最后我們指出,對于符號模式A2,A3,若記C為將它們的(n,1)元素βn換為0所得符號模式,用與定理2.2,定理2.3類似的方法可以證明C為極小譜任意的,從而A2,A3是非極小譜任意符號模式.

[1] DREW J H,JOHNSON C R,OL ESKY D D,et al.Spectrally Arbitrary Patterns[J].L inear A lgebra and its A pplications,2000,308:121-137.

[2] BRITZ T,McDONALD J J,OL ESKY D D,et al.Minimal Spectrally Arbitrary Sign Patterns[J].S IA M J Matrix A nal A ppl,2004,26:257-271.

[3] CAVERS M S,KIM I J,SHADER B L,VANDER MEUL EN K N.On Determining Minimal Spectrally Arbitrary Patterns[J].Elec J Linear A lgebra,2005,13:240-248.

[4] CAVERS M S,VANDER MEUL EN K N.Spectrally and Inertially Arbitrary Sign Patterns[J].Linear A lgebra and its A pplications,2005,394:53-72.

[5] MACGILLIVRAY G,TIFENBACH R M,et al.Spectrally Arbitrary Star Sign Patterns[J].Linear A lgebra and its A pplications,2005,400:99-119.

A Class of Spectrally Arbitrary Patterns

REN Guo-hua,GAO Yu-bin
(Department of Mathematics,North University of China,Taiyuan030051,China)

A family of sign patterns of ordernwith 2n+1 nonzero entries which are spectrally arbitrary are investigated by using the Nilpotent-Jacobian method.

sign pattern matrix;Nilpotent matrix;spectrally arbitrary pattern;minimal spectrally arbitrary pattern

O157

A

0253-2395(2010)02-0173-04

2009-01-12;

2009-02-03

國家自然科學基金(10571163);山西省自然科學基金(2007011017,2008011009)

任國花(1985-),女,山西孝義人,碩士研究生,研究方向:組合數(shù)學.E-mail:renguohua1985@126.com