李自田

PKP-方程的精確周期孤子解和雙周期解

李自田

(曲靖師范學院數(shù)學與信息科學學院,云南曲靖655011)

應用同宿測試方法研究并獲得了PKP-方程的新的精確周期孤子解和雙周期解,同時得出了該方程在點p2=4處具有衰減性.從平衡點的左側到右側,方程的解從周期孤子解衰變?yōu)殡p周期解.

周期孤子解;雙周期;同宿測試法;衰減

0 引言

在過去的二十年里,在非線性發(fā)展方程廣泛出現(xiàn)的應用領域引起了數(shù)學和物理工作者的普遍關注,許多學者在這一領域進行了卓有成效的研究.特別是在精確解的尋求和獲得方面開辟和發(fā)展了許多方法.諸如, F-擴展法[1];齊次平衡法[2]以及逆散射法[3]等.

在本文中,我們將研究如下形式的PKP-方程:其中u:Rx×Ry×Rt→R.并且:取自“+”和“-”被分別稱為PKP-I方程和PKP-II方程.

眾所周知,該模型屬于潘勒衛(wèi)不可積類型.但通過應用潘勒衛(wèi)擴展變換,我們可將該方程轉換為雙線性方程,進而通過對雙線性方程的研究,可找出并獲得該方程的解.

最近以來,該方程在諸多方面獲得了較廣泛的研究[3-6].許多學者在這些方面取得了很大的進展.文獻[5]通過應用F-擴展函數(shù)的方法研究并獲得了用橢圓函數(shù)表示的一系列周期波解;在文獻[6]中,文章的作者給出了該系統(tǒng)的N-孤子解,并得出了該系統(tǒng)可簡化為Melnikov-方程和KP-方程的特殊類型的結論.

本文通過對雙線形方程的研究,應用文獻[7]發(fā)展起來的方法,即同宿測試法,獲得了該方程的新的周期解和雙孤子解,其中的一些方法的應用和結論在解決其他同類型的問題中將具有十分深遠的意義.

1 PKP-I方程的解

首先,我們考慮PKP-I方程:

引入變換:

將(3)代入方程(2),則方程(2)可化為:

隨后,我們采用下面的變換:

將變換(5)代入方程(4),則我們得到如下形式的雙線性方程:

這里,算子“D”定義為:

引入測試函數(shù):

其中b1,b2,Ω,τ,p是實數(shù).

將(7)式代入方程(6),通過計算,我們得到如下的關系式:

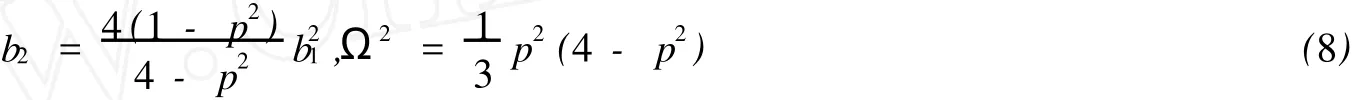
從而,將(8)代入(7)并代入(5),我們得到方程的周期孤子解:

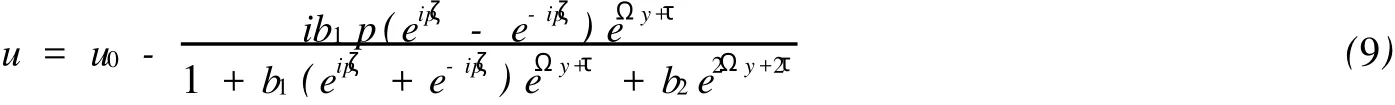
顯然,我們要求條件:

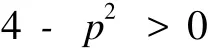
以便使式(8)中的Ω2>0,從而確保Ω能取到實數(shù).

把ζ=x+t代入(9)中,并令b2=1.從而,我們得到下列形式的周期孤子解:

2 PKP-II方程的解

考察如下形式的PKP-II方程:

應用和上面使用的相同的變換以及處理PKP-I方程所用的類似的方法,我們有雙線性方程:

設:

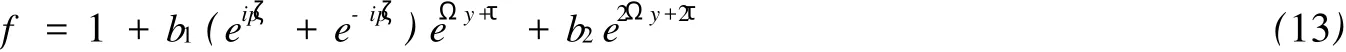
將(13)代入方程(12)并應用符號計算系統(tǒng),我們獲得了方程(11)的精確解:

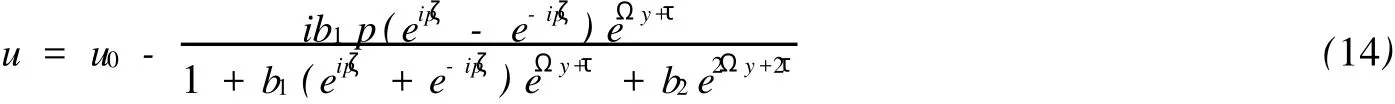
其中系數(shù)滿足:

同理,要求條件:p2>4,從而使得(15)中Ω的滿足Ω2>0.

類似地,我們取b2=1.則PKP-II方程的精確解具有如下表達式:

3 解的研究

考慮變換:(ζ,y)→(ζ,iy)

將它代入(9)并令τ=0.我們得到了一個新解,它是一個雙周期解:

比較方程(2)和方程(11),我們不難發(fā)現(xiàn),只要我們應用時間和空間的變換(ζ,y)→(ζ,iy),方程(2)可以轉換為方程(11),反之亦然.這樣,我們獲得了PKP-I方程的雙周期解:

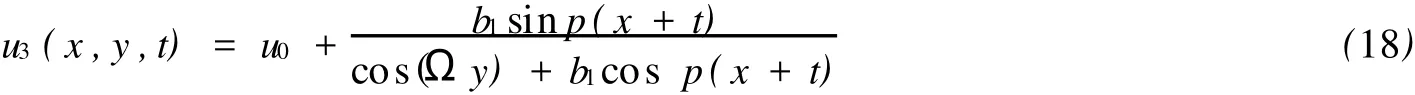
其中:p2-4>0.

注意到,(18)是PKP-I方程的奇性周期解.為了避免奇性,我們令cos(Ωy)>0和cosp(x+t)>0.

此外,同理可得PKP-II方程的雙周期解:

其中,要求條件:p2-4<0.

依據(jù)討論,我們得出結論:p2=4是PKP-I方程和PKP-II方程的唯一周期分歧點.在p2=4的兩側, PKP-I方程和PKP-II方程的解的性質發(fā)生了改變.當平衡點p2從4的一側變到另一側,周期孤子解衰變?yōu)殡p周期解.

[1] ZHANG Hui-qun.New Exact Travelling Wave Solutions for Some Nonlinear Evolution Equations,Part II[J].Chaos, Solitons and Fractals,2008,37:1328-1334.

[2] ZHOU Yu-bin,WNAG Ming-liang,MIAO Tian-de.The Periodic Wave Solutions and Solitary Wave Solutions for a Class of Nonlinear Partial Differential Equations[J].Phys Lett A,2004,323(1-2):77-88.

[3] ABLOWITZ M J,CLARKSON P A.Solitons,Nonlinear Evolution Equations and Inverse Scattering Transform[M]. Cambridge University Press,1990:8-17

[4] CARIELLO F,TABOR M.Painleve Expansions for Non-integrable Evolution Equations[J].Physica D:Nonlinear Phenomena,1989,39(1):77-94.

[5] AKHMEDIEV N,ANKIEWICZ A.Solitons,Nonlinear Pulses and Beams[M].Chapman and Hall,London,1997:124-127.

[6] ZHOU Yu-bin,WANG Ming-liang.Periodic Wave Solutions to a Coupled Kdv Equations with Variable Coefficients[J]. Phys Lett A,2003,308(1):31-36.

[7] DAI Zheng-de,LI Shao-ling,ZHU Ai-jun.Singular Periodic Soliton Solutions and Resonance for the Kadomtsev-Petviashvili Equation[J].Chaos,Solitons and Fractals,2007,34(4):1148.

Exact Periodic Soliton Solution and Double Periodic Solution to PKP-equations

LI Zi-tian
(College of Mathematics and Inf ormation Science,Qujing Normal University,Qujing655011,China)

The periodic soliton and the double periodic solutions to PKP-equation are obtained by using homoclinic test method.Mean while,we also find that the equation has the properties of degeneration atp2= 4.When the equilibriumpvaries from one side ofp2=4 to the other side,the periodic soliton solution changes into a doubly periodic solution.

periodic soliton solutions;double periodic;homoclinic test method;degeneration

O175.23

A

0253-2395(2010)02-0166-03

2009-04-07

國家自然科學基金(10361007,10661002);云南省教育廳科學研究基金項目(08Y0302);曲靖師范學院科研基金(2008MS018;2009MS007)

李自田(1972-),男,碩士,講師,主要從事偏微分方程研究.E-mail:lizitian88@163.com