周建榮

(佛山科學(xué)技術(shù)學(xué)院 理學(xué)院數(shù)學(xué)系, 廣東 佛山 528000)

周建榮

(佛山科學(xué)技術(shù)學(xué)院 理學(xué)院數(shù)學(xué)系, 廣東 佛山 528000)

應(yīng)用展開(kāi)方法導(dǎo)出了Fitzhugh-Nagumo非線性方程新的孤波解.

孤波解;展開(kāi)方法; Fitzhugh-Nagumo方程

近年來(lái), 尋求非線性方程的行波解已引起人們的極大興趣. 目前, 求解非線性方程比較成功的方法有齊次平衡法[5], 逆散射方法[2], Hopf-Cole變換法[12], Exp函數(shù)展開(kāi)法[13], 雙曲正切函數(shù)展開(kāi)法[3,11], Sine-Cosine方法[15], 輔助方程法[14], 雙曲函數(shù)法[4], 第一積分法[1,9]和雙線性法[6], 等等.

新的孤波解, 其中δ為實(shí)常數(shù).

這里的求導(dǎo)是關(guān)于波變量ξ.

應(yīng)用方程(4), 從(3)式可得

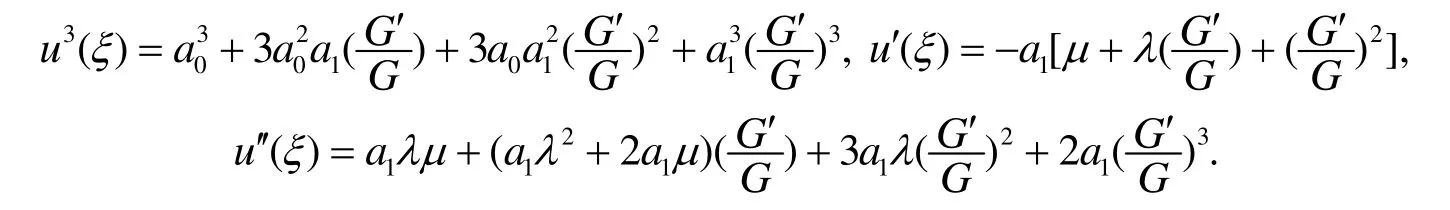
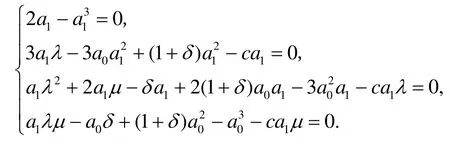
應(yīng)用數(shù)學(xué)軟件Maple解此方程組得三組解:

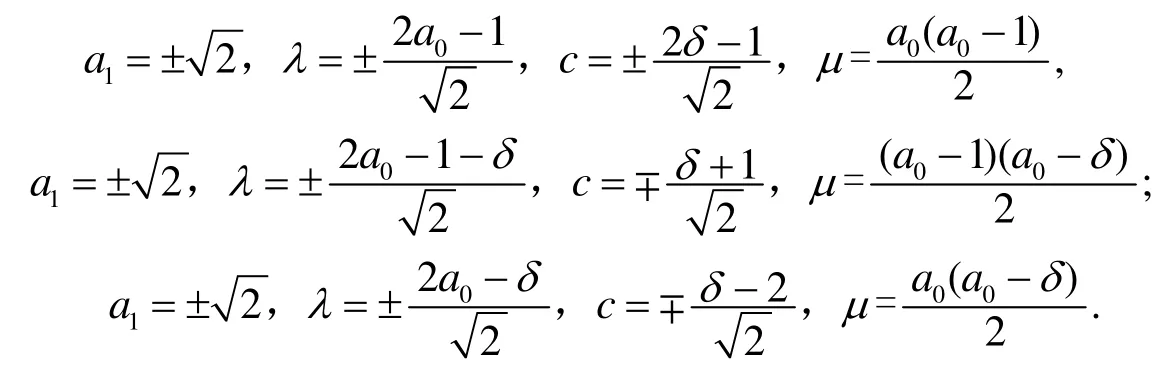
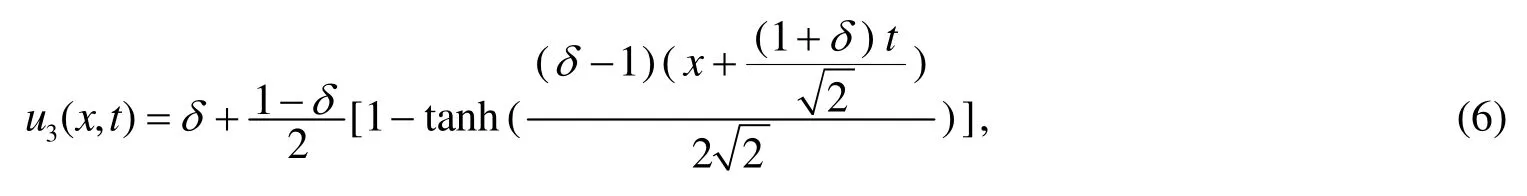
(6)～(13)式是在文[11]中通過(guò)Tanh-Coth方法已經(jīng)得到的孤波解.

[1] S. Abbasbandy, A. Shirzadi.The first integral method for modified Benjamin–Bona–Mahony equation[J]. Commun Nonlinear Sci Numer Simulat 2010, (15): 1759～1764

[2] Ablowitz MJ, Clarkson PA.Solitons,nonlinear evolution equations and inverse scattering transfor[M]. Cambridge: Cambridge University Press, 1990

[3] Bekir A.Applications of the extended tanh method for coupled nonlinear evolution equations[J]. Commun Nonlinear Sci Numer Simulat 2008, 13(9): 1748～1757

[4] Chaofa Deng.New exact solutions to the Zakharov–Kuznetsov equation and its generalized form[J]. Commun Nonlinear Sci Numer Simulat 2010, 15: 857～868

[5] Fan E, Zhang H.A note on the homogeneous balance method[J]. Phys. Lett. A 1998, (246): 403～406

[6] Hirota R.Direct method of finding exact solutions of nonlinear evolution equations[J]. In: R. Bullough , P. Caudrey(Eds.), Backlund Transformations, Springer, Berlin 1980: 1157～1175

[7] Hai-Ling Lü, Xi-Qiang Liu, Lei Niu.A generalized-expansion method and its applications to nonlinear evolution equations[J].Applied Mathematics

and Computation 2010, (215): 3811～3816

[8] F. Tascan, A. Bekir.Travelling wave solutions of the Cahn-Allen equation by using first integral method[J]. Applied Mathematics and Computation 2009, 207: 279～282

[9] F. Tascan, A. Bekir, M. Koparan.Travelling wave solutions of nonlinear evolution equations by using the first integral method[J]. Communications in Nonlinear Science and Numerical Simulation 2009, 14: 1810～1815

[10] Wang ML, Li X, Zhang J.The-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J]. Phys. Lett. A 2008, 372(4): 417～423

[11] Wazwaz AM.The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations[J]. Appl. Math. Coptut. 2007, 188: 1467～1475

[12] Wazwaz AM.Multiple soliton solutions for a (2 + 1)-dimensional integrable KdV6 equation[J]. Commun Nonlinear Sci Numer Simulat 2010, 15: 1466～1472

[13] Xu F.Application of Exp-function method to symmetric regularized long wave (SRLW) equation[J]. Phys. Lett. A 2008, 372(3): 252～257

[14] Yunxi Guo, Shaoyong Lai.New exact solutions for an (N+1)-dimensional generalized Boussinesq equation[J]. Nonlinear Analysis 2010, 72: 2863～2873

[15] Yusufoglu E, Bekir A, A, Alp M.Periodic and solitary wave solutions of Kawahara and modified Kawahara equations by using sine-cosine method[J]. Chaos, Solitons & Fractals 2008, 37(4): 1193～1197

ZHOU Jian-rong
(Department of Mathematics, Foshan University, Foshan 528000, China)

The-expansion method is used to construct new solitary wave solutions of Fitzhugh-Nagumo equation.

solitary wave solutions;-expansion method; Fitzhugh-Nagumo equation

O175.29

A

1672-5298(2010)03-0021-03

2010-01-15

廣東高校優(yōu)秀青年創(chuàng)新人才培育項(xiàng)目(LYM08101)

周建榮(1978- ), 男, 湖南永州人, 博士, 佛山科學(xué)技術(shù)學(xué)院理學(xué)院數(shù)學(xué)系講師. 主要研究方向: 漸近分析及非線性問(wèn)題