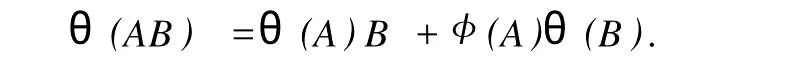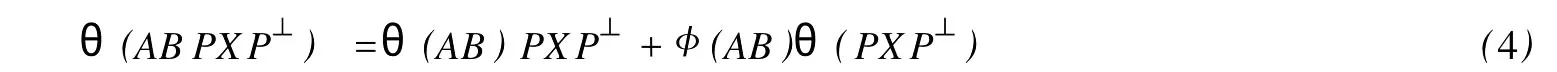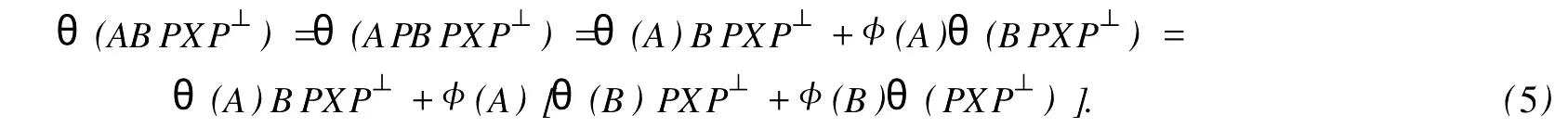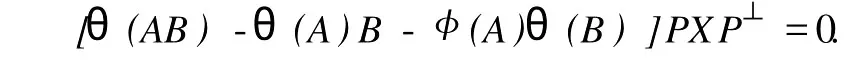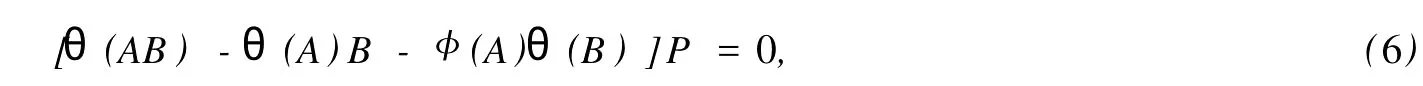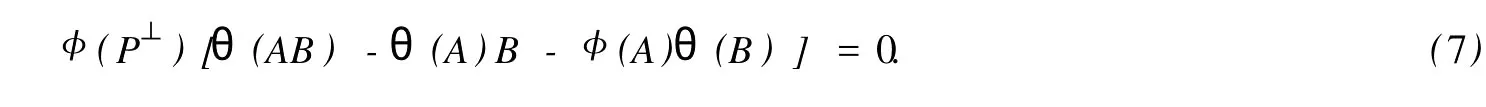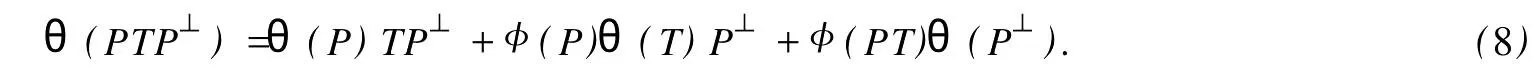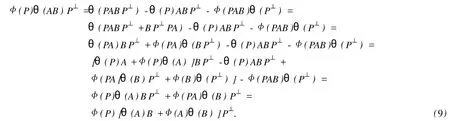套代數(shù)上的2-局部φ-導(dǎo)子*
吳瑞華,呂 川
(中國石油大學(xué)數(shù)學(xué)與計算科學(xué)學(xué)院,山東東營257061)
套代數(shù)上的2-局部φ-導(dǎo)子*
吳瑞華,呂 川
(中國石油大學(xué)數(shù)學(xué)與計算科學(xué)學(xué)院,山東東營257061)
從代數(shù)的結(jié)構(gòu)和映射的特征出發(fā),研究了套代數(shù)上的2-局部φ-導(dǎo)子,證明了套代數(shù)上的2-局部φ-導(dǎo)子都是φ-導(dǎo)子.
2-局部φ-導(dǎo)子;φ-導(dǎo)子;套代數(shù)
引言
首先給出幾個定義,設(shè)A是一個代數(shù),φ是A上的一個自同構(gòu),η是A上的一個線性映射.如果對任意的a∈A有η(a2)=η(a)a+φ(a)η(a),則稱η是一個Jordanφ-導(dǎo)子;如果對任意的a,b∈A有η(ab)= η(a)b+φ(a)η(b),則稱η是一個φ-導(dǎo)子;如果對任意的a∈A,都存在A上的一個φ-導(dǎo)子ηa(依賴于a)使得η(a)=ηa(a),則稱η是一個局部φ-導(dǎo)子;如果對任意的a,b∈A都存在A上的一個φ-導(dǎo)子ηa,b(依賴于a,b)使得η(a)=ηa,b(a);η(b)ηa,b則稱η是一個2-局部φ-導(dǎo)子.Kadision[1]首次研究了算子代數(shù)的局部映射問題,局部導(dǎo)子和2-局部導(dǎo)子的概念是由Kadision[1]、Larson Sourour[2]和Semrl[3]引入的,在此研究一類更一般的映射2-局部φ-導(dǎo)子.由于局部映射不僅對算子代數(shù)的上同調(diào)群起著十分重要的作用,而且為人們設(shè)計滿足不同需要和具有特殊性質(zhì)的映射從而解決相關(guān)問題提供了一種可能,因此它已成為算子理論和算子代數(shù)的重要研究課題之一,吸引了一大批數(shù)學(xué)家投身其中,并出現(xiàn)了豐富的相關(guān)研究成果[1,2,4~6].在過去的幾十年里,φ-導(dǎo)子已在純代數(shù)中進(jìn)行了廣泛的研究[7~11]并應(yīng)用于相關(guān)領(lǐng)域[12].本文研究一類更一般的映射2-局部φ-導(dǎo)子.導(dǎo)子成立的某些結(jié)論2-局部φ-導(dǎo)子是否也成立?在此主要研究套代數(shù)上的2-局部φ-導(dǎo)子何時成為φ-導(dǎo)子.
設(shè)H是可分Hilbert空間,B(H)表示H上的全體有界線性算子,B(H)上的套N是指B(H)中的一個全序投影族,它包含0和I且在強(qiáng)算子拓?fù)湎率情]的.對N中的每一個投影P,記P+=inf(Q∈N◇Q>P}和P-=sup{Q∈N◇Q 以下總假設(shè)φ是τ(N)上的自同構(gòu),θ是τ(N)上的2-局部-φ-導(dǎo)子. 引理1 (a)如果A,B∈τ(N)使得AB=0,那么θ(A)B+φ(A)θ(B)=0. (b)對任意的A,X,B∈τ(N)有: 證明 (a)對任意的A,B∈τ(N)且AB=0,由δ的定義知,存在一個依賴于A,B的φ-導(dǎo)子θA,B滿足θ(A)=θA,B(A),θ(B)=θA,B(B).因此就有 (b)設(shè)A∈τ(N),由θ的性質(zhì),存在一個依賴于A,A2的φ-導(dǎo)子θA,A2滿足θ(A)=θA,A2(A),θ(B)=θA,A2(B).所以有 在上式中用A+X替代A可得 再在上式中用AX+XA替代X則得 將上式中的A替換為A+B,則對任意的A,X,B∈τ(N)即可證得 證畢. 引理2 如果P是N中的投影,那么對任意的X∈B(H)有 證明 對任意的P∈N,X∈B(H),由引理1得 另一方面 這說明有φ(P)θ(PXP⊥)=φ(P)θ(PXP⊥)P⊥+φ(PXP⊥)θ(P⊥). 因此得θ(PXP⊥)=φ(P)θ(PXP⊥)P⊥+θ(P)PXP⊥+φ(PXP⊥)θ(P⊥).證畢. 引理3 對任意的A∈τ(N)和P∈N都有 證明 由引理1(b)得 所以φ(P)θ(PAP⊥)P⊥=θ(P)θ(P)AP⊥+φ(P)θ(A)P⊥+φ(PA)θ(P⊥)P⊥,由引理2有 由式(1),(2),(3)得θ(PA)=θ(PAP)+θ(PAP⊥)=θ(P)A+φ(P)θ(A)和 θ(AP⊥)=θ(PAP⊥)+θ(P⊥AP⊥)=θ(A)P⊥+φ(A)θ(P⊥).證畢. 在引理3中令A(yù)=I可得以下推論: 引理4 如果P是N中的投影,那么對任意的A∈τ(N),X∈B(H),有 證明 設(shè)P∈N任意的A∈τ(N),X∈B(H),T∈B(H),引理1~3說明 同理可證(b)式也成立.證畢. 下面的定理1是本文的主要結(jié)果 定理1 設(shè)N是B(H)中的任意一個套,φ是τ(N)上的自同構(gòu),θ是τ(N)上的一個2-局部φ-導(dǎo)子(沒有連續(xù)性的假設(shè)).則對任意的Α,Β∈τ(N)有 此定理說明了套代數(shù)上的任意2-局部φ-導(dǎo)子都是φ-導(dǎo)子. 證明 設(shè)A,B∈τ(N),P為N中的一個固定非平凡投影.對任意的X∈B(H)由引理4(a)得 另一方面,再由引理4(a)得 據(jù)式(4),(5)對任意的X∈B(H)有 因此, 同理由引理4(b),得 由引理3,任意T∈τ(N)有 從而由式(8)和引理1,3有 由式(6),(7),(9),對任意的A,B∈τ(N),就有θ(AB)=θ(A)B+φ(A)θ(B).也就是說明θ是一個φ-導(dǎo)子.證畢. 參考文獻(xiàn): [1]Kadision R V.Local derivation[J].Algebra,1990,130:494-509. [2]Larson D R,SourourA R.Local derivations and local automorphis ms of[J].Proceedings Symposia in PureMathematics,1990, 51:187-194. [3]Semrl P.Local automophis ms and derivations on[J].Proc Amer.Math.Soc.,1997,125:2677-2680. [4]BresarM,Semrl P.Mappingswhich preserve idempotents,local automorphis ms,and local derivation[J].Canad Math,1993, 45:483-496. [5]Crist R L.Local derivation on operator algebras[J].Funct.Anal,1996,135:76-92. [6]Larson D R.Reflexivity,algebra reflexivity,and linear interpolation[J].Amer.Math,1988,110:283-229. [7]BresarM,VillenaA R.The noncommutative Singer-Wermer conjecture andφ-derivations[J].LondonMath.Soc,2002,66: 710-720. [8]Bergen J.Skew derivationswhose invariants satisfy a polynomial identity[J].Algebra,2000,228:710-737. [9]Chuang C L.Identitieswith skew derivations[J].Algebra,2000,224:292-335. [10]Chuang C L,Lee T K.Algebraic-skew derivations[J].Algebra,2004,282:1-22. [11]Chuang C L,Lee T K.Identitieswith a single skew derivation[J].Algebra,2005,288:59-77. [12]BresarM,Fosner A,FosnerM.A Kleinecke-Shirokov type condition with Jordan automorphisms[J].Studia Math,2001, 147:237-242. 2-Local Skew-Derivation of Nest Algebras WU Rui-hua,LüChuan (School ofMathematics and Computational Science,China University of Petroleum,Dongying Shandong 257061,China) A study on the 2-localφ-derivation of nest algebras is made by using the characteristics of the concepts and mappings of algebras.It is proved that every 2-localφ-derivation of nest algebras is aφ-derivation. 2-localφ-derivation;φ-derivation;nest algebra book=5,ebook=383 O 177.1 A 1673-2103(2010)05-0005-04 2010-07-18 中國石油大學(xué)自主創(chuàng)新科研計劃項目(09CX04065A) 吳瑞華(1981-),女,山東臨沂人,講師,碩士,研究方向:算子理論與算子代數(shù).1 預(yù)備知識
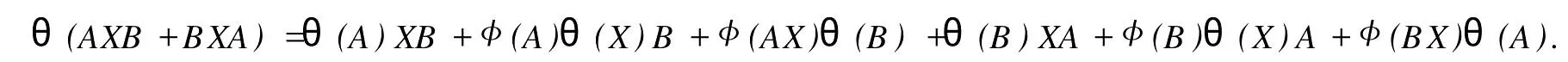
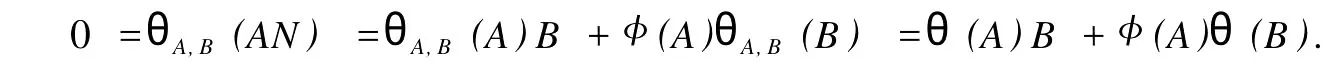
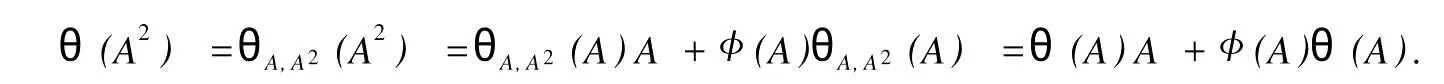
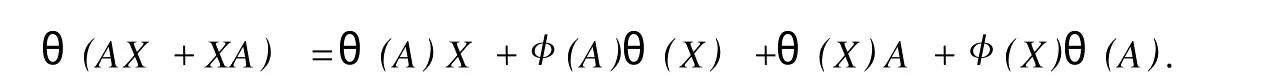
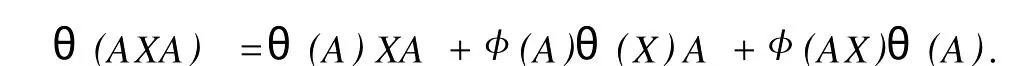
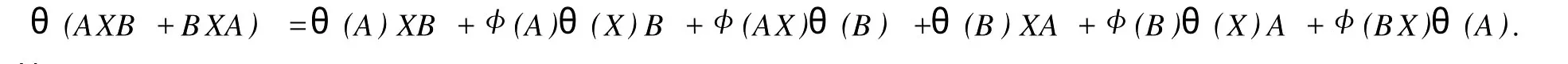
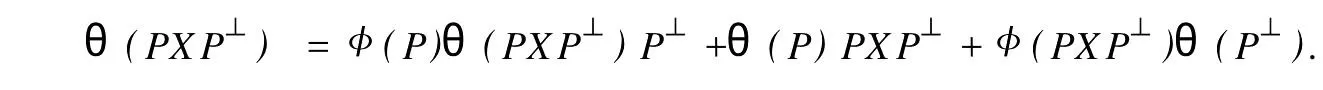
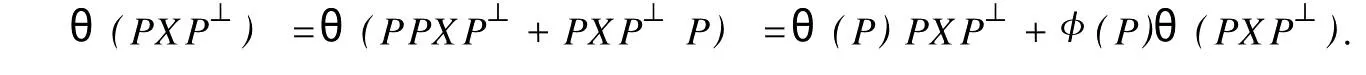
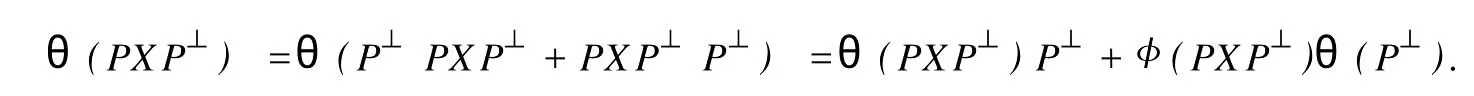

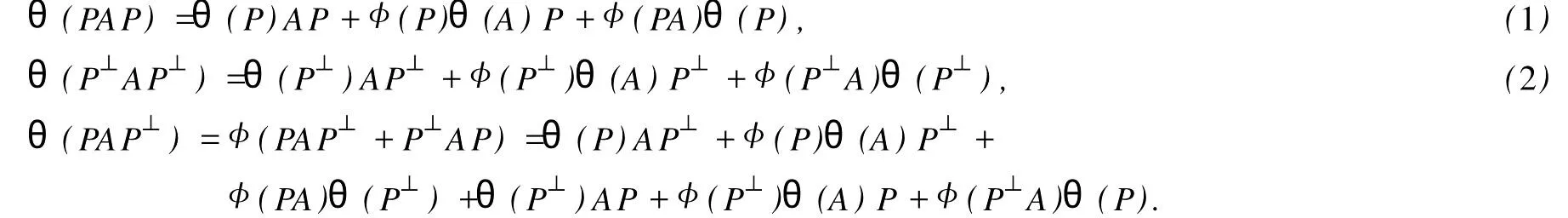
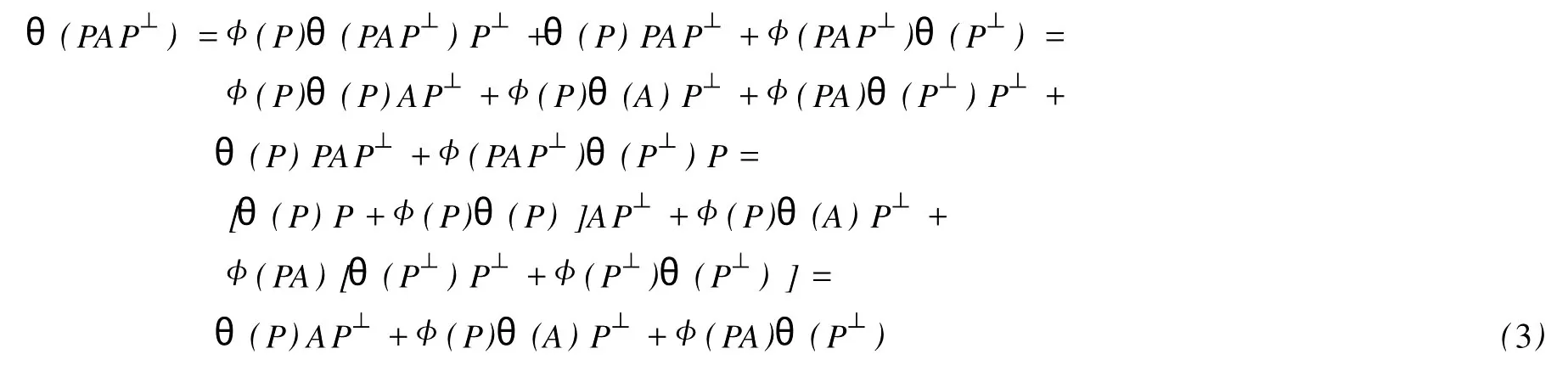
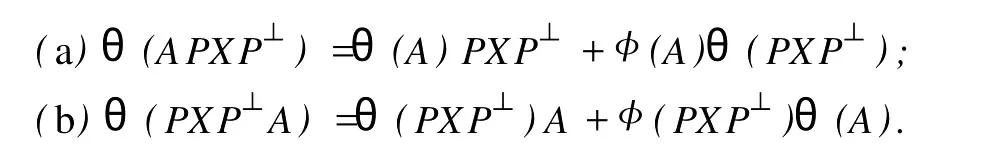
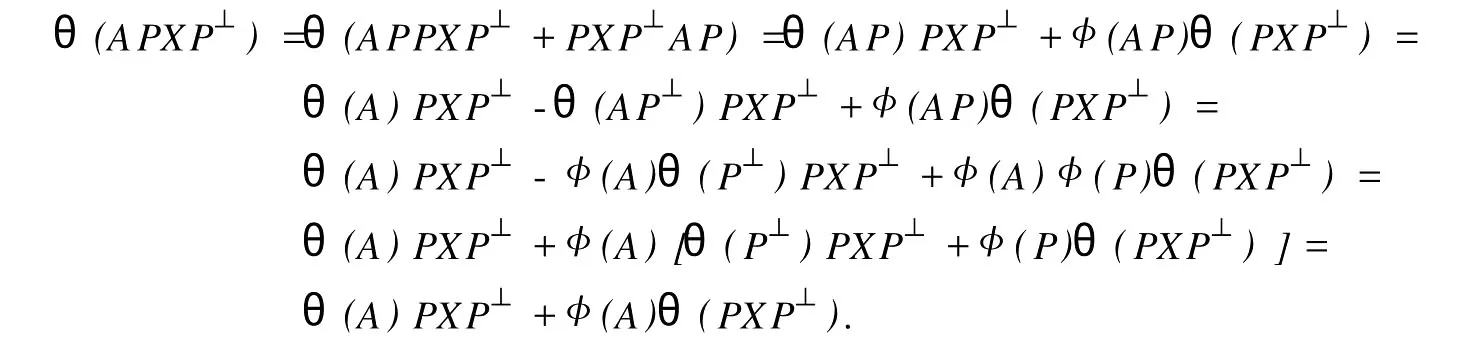
2 主要結(jié)果