WANG Lin (王琳), HAO Xiaosong (郝小松), ZHENG Lan (鄭嵐) and CHEN Kaixun (陳開勛),*

?

Phase Equilibrium of Isobutanol in Supercritical CO2

WANG Lin (王琳)1,2, HAO Xiaosong (郝小松)1, ZHENG Lan (鄭嵐)1and CHEN Kaixun (陳開勛)1,*

1Chemical Engineering College, Northwest University, Xi’an 710069, China2Chemistry and Pharmaceutical Engineering Coll ege, Nanyang Normal University, Nanyang 473061, China

Vapor-liquid phase equilibrium data including composition, densities, molar volume and equilibrium constant of isobutanol in supercritical carbon dioxide from 313.2 K to 353.2 K were measured in a variable-volume visual cell. The properties of critical point were obtained by extrapolation. The results showed that critical temperature, critical pressure and critical compressibility factor of CO2-isobutanol system decreased with the increase of critical CO2content. The phase equilibrium model was established by Peng-Robinson equation of state and van der Waals-2 mixing regulation, and model parameters were determined by optimization calculation of nonlinear least square method. The correlation between calculated values and the experimental data showed good agreement.

supercritical carbon dioxide, isobutanol, phase equilibrium model, critical property

1 INTRODUCTION

Supercritical fluid extraction technique (SCFE) is used widely in many processes as a new separation method, such as in removal of trace impurities, recovery of substance having high additional value and thermal sensitivity. CO2is the most commonly used supercritical fluid because of its toxicological inertness, low critical temperature, low cost and small impact on the earth’s environment [1-3]. Alcohol existing widely in fermentation wasted water is often used as entrainer to control the polarity of supercritical fluid, or as a modifier for supercritical fluid chromatography [4]. Thus, the study on supercritical CO2and alcohol is becoming increasingly popular. Vapor-liquid equilibrium properties at high pressures are required for engineering application such as in the design and operation of separation processes. There were some phase equilibrium reports on alcohol in CO2up to now [5-9], but fewer studies were on isobutanol in supercritical CO2[10]. In the present study, new vapor-liquid equilibrium data of isobutanol in CO2from 313.2 K to 353.2 K were measured in a variable-volume visual high pressure cell. Meanwhile, Peng-Robinson equation of state and van der Waals mixing rule were applied to predict vapor- liquid equilibria for CO2+isobutanol binary system.

2 EXPERIMENTAL

2.1 Materials and apparatus

2.1.1

Carbon dioxide was supplied by Shanxi Xinghua BOC Ltd. with a purity of 99.99%. Isobutanol(purity> 99%, by mass) was analytical reagent.

2.1.2

A schematic diagram of a variable-volume visual cell was shown in Fig. 1. The cell was produced by Hai’an Petroleum Research Instrument Plant, Nantong, Jiangsu. The apparatus had two visual windows and its internal maximum volume was 60 ml. The maximum operating temperature and pressure of the apparatus were 423 K with an accuracy of 0.1 K and 20 MPa with an accuracy of 0.01 MPa, respectively. The main parts of the apparatus were a variable volume cell, piston and screw-driven pump. The equilibrium pressure in the cell was measured by a differential pressure gauge; cell temperature was controlled by HA120-50-01 constant temperature liquid bath controller and measured by XT-7000 intelligent temperature regulation indicator. A magnetic stirrer was used for mixing the fluid in the cell.

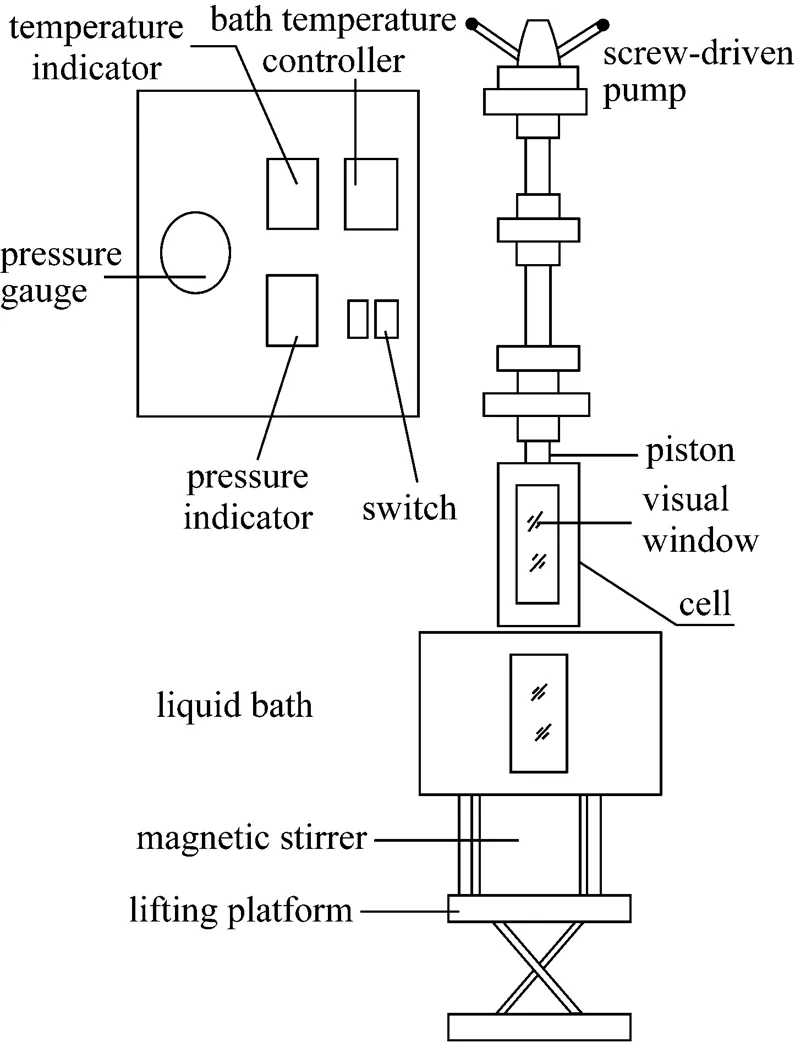
Figure 1 The schematic diagram of experimental apparatus

2.2 Experimental procedure

Before each experiment, the piston was moved to the upper dead position, thus, the volume of the view cell was made maximal. The entire internal loop of the apparatus including the equilibrium cell was rinsed several times with carbon dioxide. Then, the equilibrium cell was evacuated with a vacuum pump. The cell was charged with a given amount of isobutanol. Then, it was slightly pressurized with carbon dioxide to the initial pressure and was heated to the temperature. Different pressures were reached by different initial pressures and moving piston to different places. Once the pressure and temperature were adjusted to pre-set values, the mixture was stirred for a few hours. Then, the stirrer was switched off and after about one hour the coexisting phases were separated completely. Phase interface could be observed by visual window. Samples of vapor and liquid phase were collected respectively with small steel vessel by their own sampling valve.

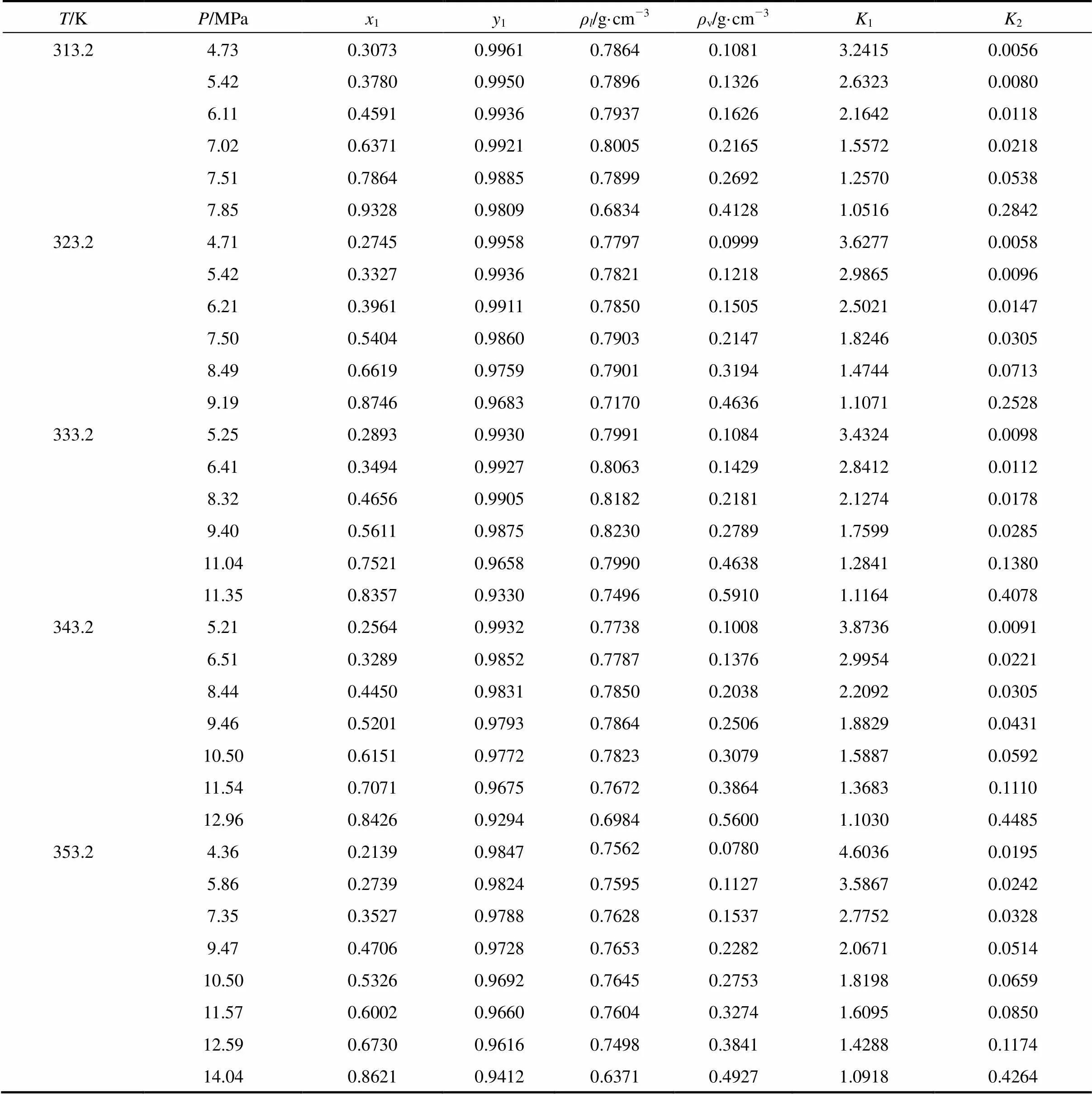
Table 1 Vapor-liquid phase equilibrium data of isobutanol(2) in CO2(1)

2.3 Analytical method

The analytical method was applied to determine the phase compositions at different temperatures and different pressures. The small sampling steel vessel was placed in an ice-water bath and connected with a desorption tank by capillary and needle-type valve. After the desorption tank was evacuated, carbon dioxide was desorbed to desorption tank slowly until pressure of the tank did not change; then, the temperature and pressure were recorded. Because the pressure in the desorption tank was far below the atmosphere pressure, the mass of CO2could be calculated by equation of state of ideal gas. The mass of isobutanol was equal to the sample mass minus CO2mass. Finally the molar fractions of two phases could be obtained at given temperature and pressure.

3 RESULTS AND DISCUSSION

3.1 Experimental data

Vapor-liquid equilibrium data of isobutanol in CO2at 313.2 K, 323.2 K, 333.2 K, 343.2 K, 353.2 K were measured and listed in Table 1, where1and2were equilibrium constant of CO2(1) and isobutanol(2), respectively.

3.2 Results and discussion

Figure 2 indicated--diagram of CO2-isobutanol at different temperatures. As could be showed from Fig. 2, solubility of CO2would increase in liquid phase and would decrease in vapor phase with increasing pressure at the same temperature. At the same pressure, the solubility of CO2would decrease in liquid phase with increasing temperature, but the solubility of isobutanol would increase in vapor phase because its vapor pressure increased with increasing temperature. Since all thermodynamics properties of vapor phase and liquid phase were equal completely at critical point [11, 12], the composition of vapor and liquid phase must be equal completely at the critical point. Thus, critical point could be obtained by extrapolating vapor and liquid curve to their inflexion point.

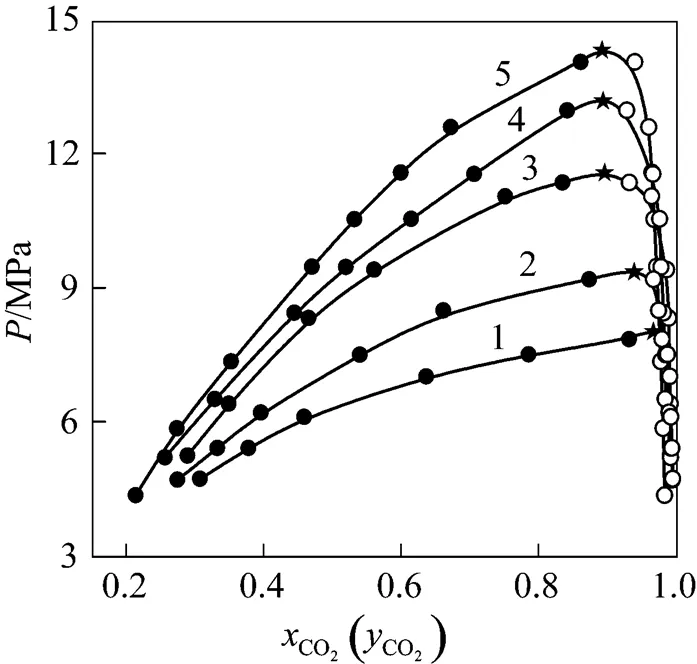
Figure 2--diagram of CO2-isobutanol at different temperatures ●?liquid phase;○?vapor phase;★?estimated critical points/K: 1—313.2; 2—323.2; 3—333.2; 4—343.2; 5—353.2

Figure 3-diagram of CO2-isobutanol at different temperatures●?liquid phase;○?vapor phase/K: 1—313.2; 2—323.2; 3—333.2; 4—343.2; 5—353.2

Figure 4 was the-diagram at different temperatures. The results in Fig. 4 showed that the density of the liquid phase decreased with the increasing pressure owing to enhancement of CO2content in liquid phase, but the density of vapor phase increased with increasing pressure. Thus, the densities of vapor and liquid phase would approach gradually and the pressure and density corresponding to the intersecting point of two curves were critical pressure and critical density, respectively.

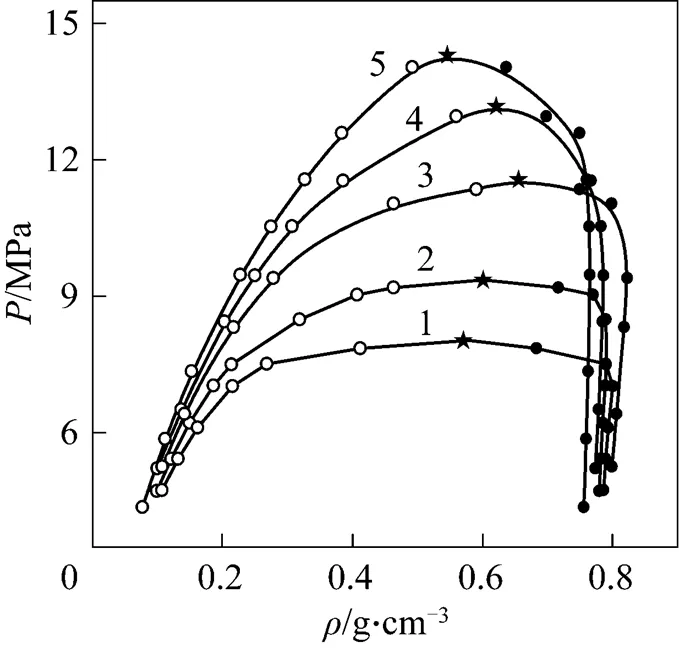
Figure 4-diagram of CO2-isobutanol at different temperatures ●?liquid phase;○?vapor phase; ★?calculated critical points/K: 1—313.2; 2—323.2; 3—333.2; 4—343.2; 5—353.2

The correspondingm--diagram was drawn in Fig. 5, where the thin line indicated isopiestic conjugating line. The intersecting point of vapor phase and liquid phase curves corresponded to critical molar volume and critical composition.

The critical values obtained from the above figures were summarized in Table 2, in which the critical properties of pure components readily available in the calculation were from literature [13].

The results in Table 2 showed that the critical temperature of CO2-isobutanol dinary system was between critical temperatures of two pure components and critical pressure was above any of pure components. Moreover, critical temperature and critical pressure decreased with increasing critical composition of CO2, but critical density had a maximum value and critical molar volume had a minimum value in the measurement range.

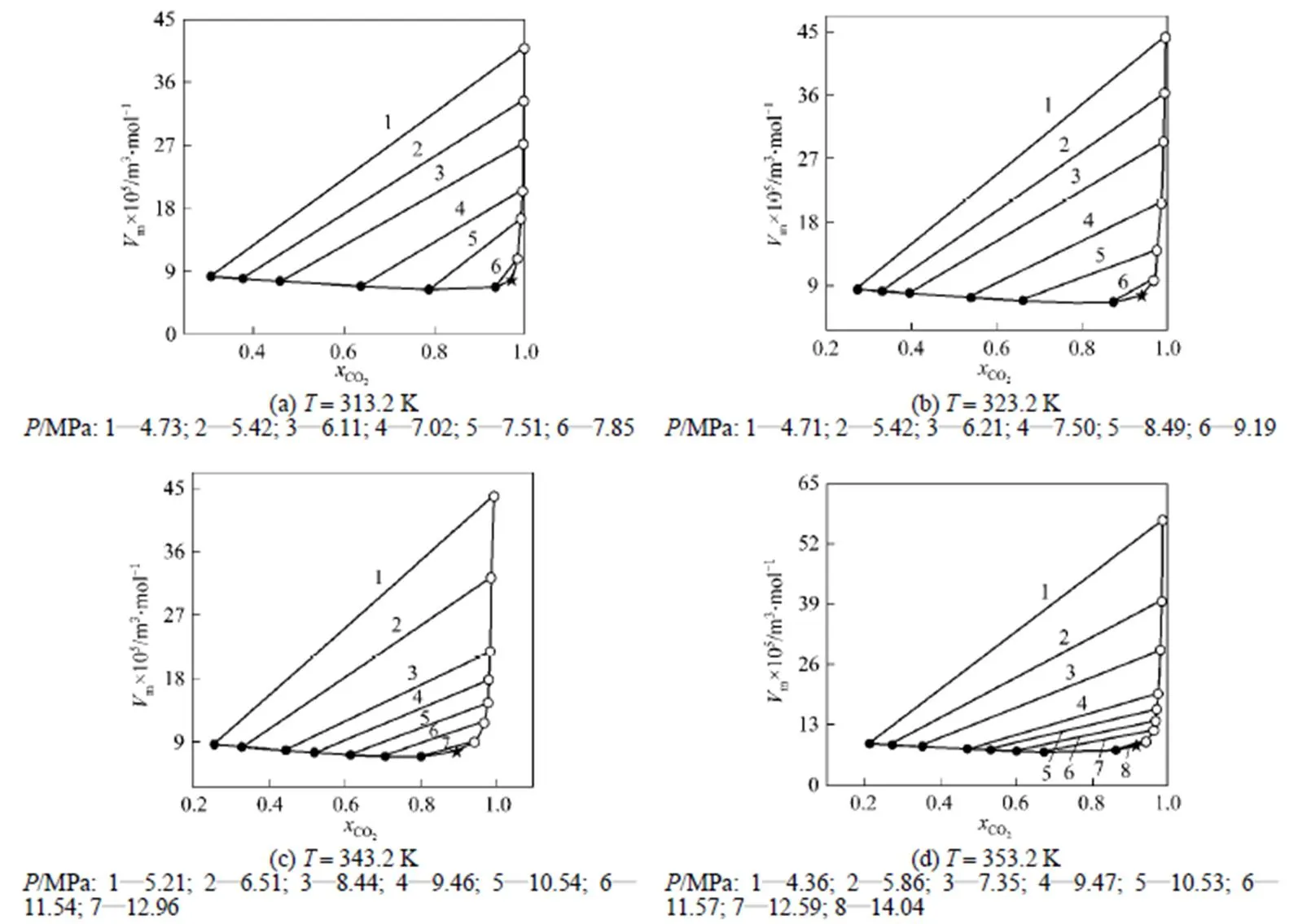
Figure 5m--diagram of CO2-isobutanol at different temperature●?liquid phase; ○?vapor phase; ★?calculated critical points

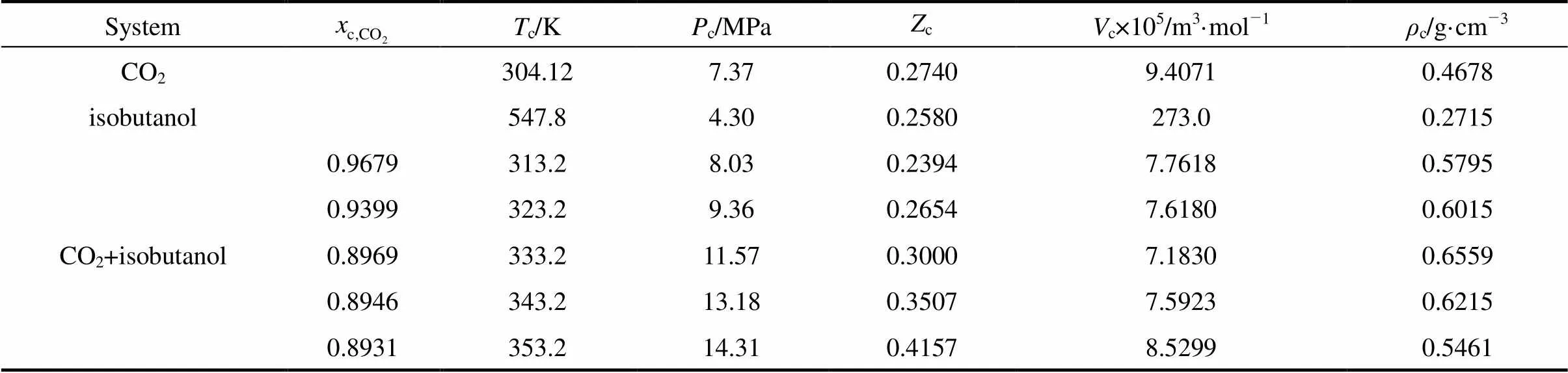
Table 2 The critical values of CO2-isobutanol

4 CORRELATION

If the system arrived to equilibrium state, the partial fugacities were equal for each component in all the phases [14-16].

For allcomponents, CO2and isobutanol, the fugacity could be calculated using the fugacity coefficient:

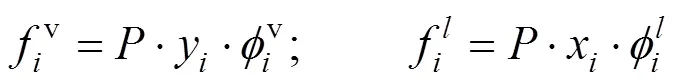
The fugacity coefficient was calculated with Eq. (4):

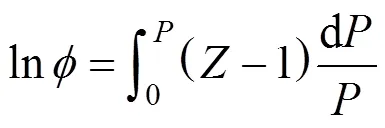
Thus, the pressure dependence of thecompressibility factor was necessary. This could be derived from an equation of state (EOS).

In the work, the cubic Peng-Robinson equation of state, van der Waals-1 and van der Waals-2 mixing rule were chosen to describe vapor-liquid equilibria.

4.1 Phase equilibrium description model [17-22]

The expansion of compressibility factorof Peng-Robinson equation of state (PREOS) was Eq.(5)

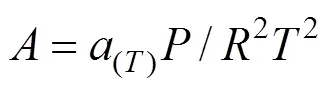
The constantsandwere calculated from the pure fluid critical data:

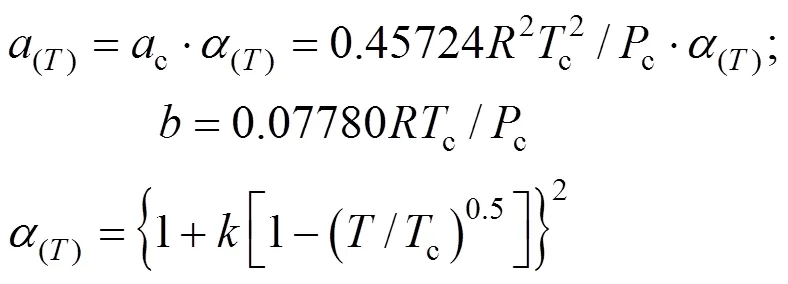
The parameterwas calculated using, the Pitzer acentric factor:

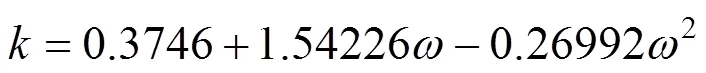
van der Waals-1 mixing rule was:

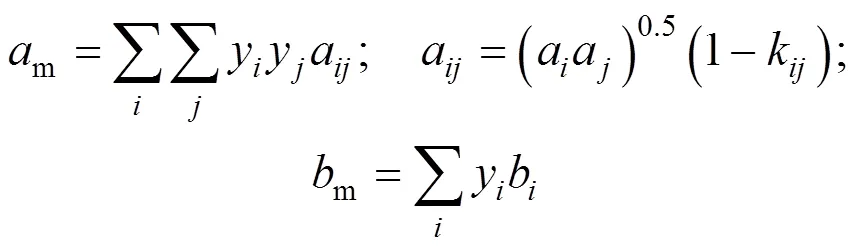
van der Waals-2 mixing rule was:

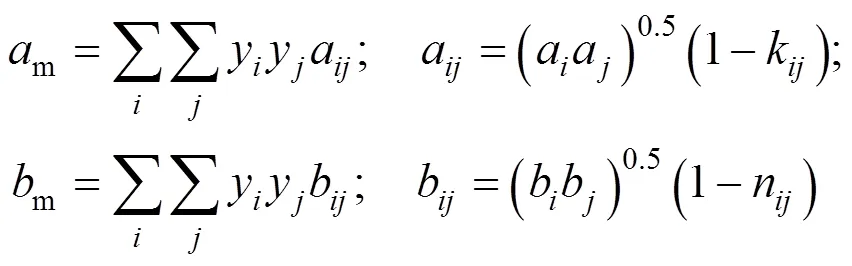
The integral equation of fugacity coefficient with PR and van der Waals-1 mixing rule(PR-1) was calculated by the following formula:

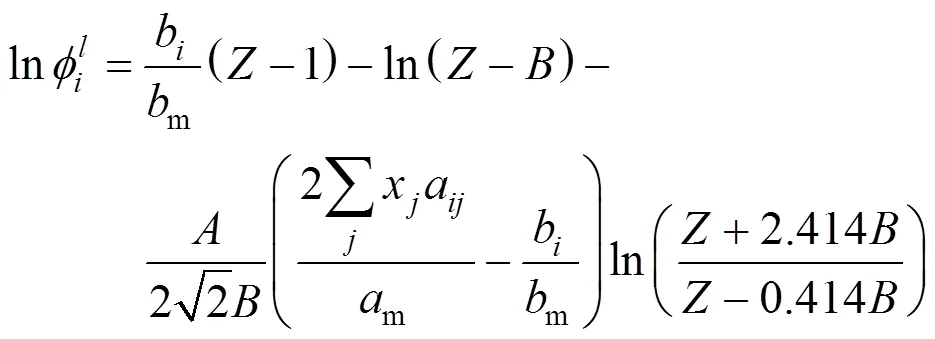
The integral equation of fugacity coefficient with PR and van der Waals-2 mixing rule(PR-2) was calculated by the following formula:

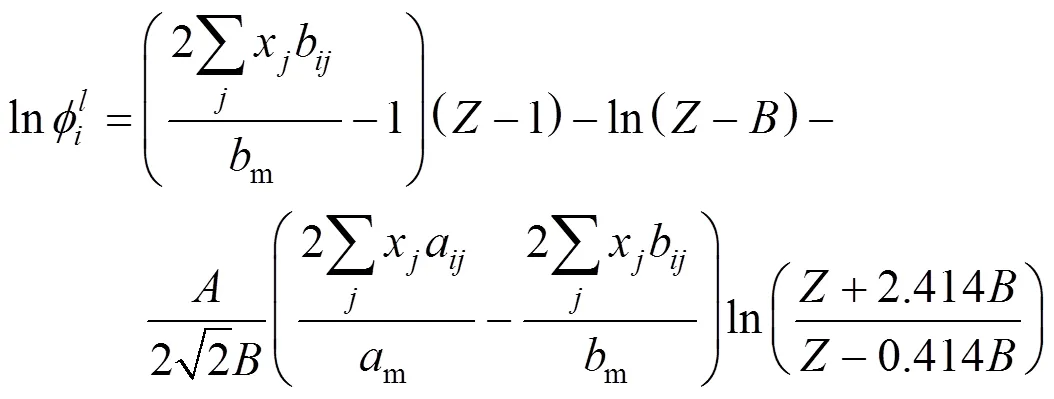
The objective function applied in the work was:

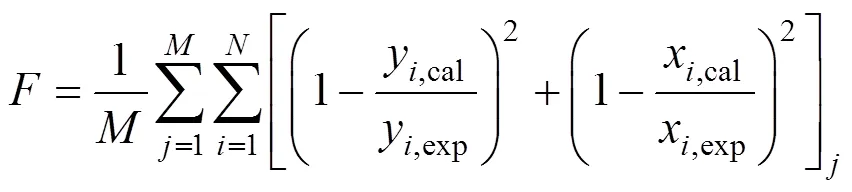
Whereandwere the number of acquired phase equilibrium and the number of components in the system, respectively.was the objective function.

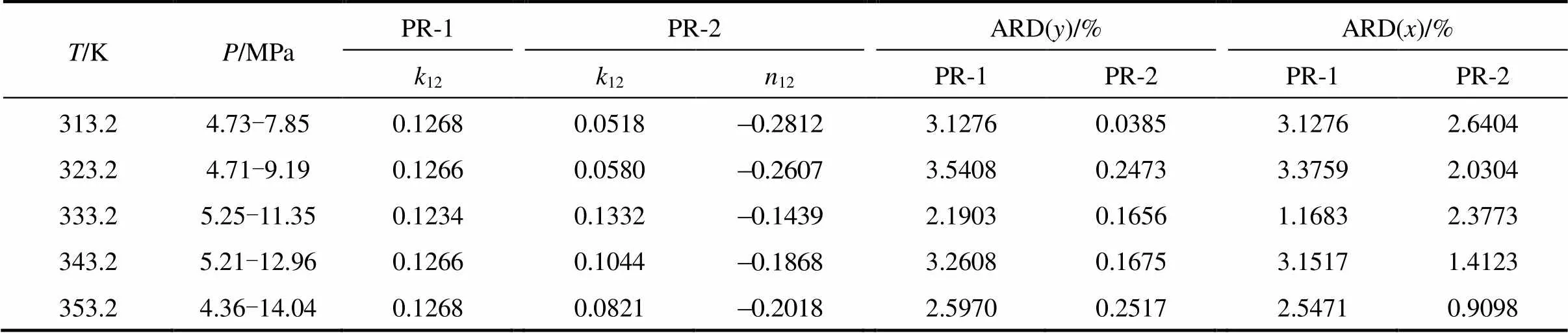
Table 3 Vapor-liquid phase equilibrium calculated results of CO2(1)+isobutanol(2) system

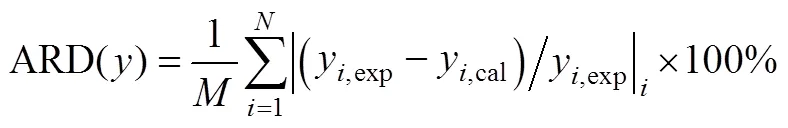
4.2 Calculated results and discussion

The simplex optimization was done with metlab7.0 software according to the above-mentioned equations. The optimized model parameters and deviation analysis were summarized in Table 3.

The results in Table 3 showed that a bigger deviation produced from the value with PR-1 model than from PR-2. Deviation analysis of molar fraction of vapor and liquid in Table 3 also showed that the adaptable model was influenced significantly by mixing rule, and Peng-Robinson equation of state and van der Waals-2 mixing regulation could be applied to better understanding of the phase behavior for CO2+isobutanol dinary system at high pressures and near-critical area. Due to the density of solution increased at high pressure and near-critical area, the short-course repulsive between molecules played a dominant role. It was necessary to revise the parameters representing molecule volume or molecule diameter. Accordingly, van der Waals-2 mixing rule including the two revising parameters was adaptable.

5 CONCLUSIONS

The phase equilibrium composition, density, molar volume and equilibrium constant of isobutanol in CO2were measured in a variable-volume visual cell from 313.2 K to 353.2 K. The phase equilibrium model was established by Peng-Robinson equation of state and van der Waals-2 mixing regulation. Consequently, the prediction model was expected to be a useful tool for the process design and operations of isobutanol from solutions including isobutanol with supercritical CO2.

NOMENCLATURE

ARD average relative deviation

f,φpartial fugacity and partial fugacity coefficient ofcomponent

12,12dinary action parameter

pressure, MPa

temperature, K

mmolar volume, cm3·mol－1

xmolar fraction ofcomponent in liquid phase

ymolar fraction ofcomponent in vapor phase

compressibility factor

density, g·cm－3

Superscripts

liquid phase

v vapor phase

Subscripts

c critical point

cal calculated value

exp experimental data

1 Zhu, Z.Q., “Supercritical fluid extraction”, Supercritical Fluid Technology—The Principle and Application, Chemical Industry Press, Beijing (2001). (in Chinese)

2 Kamel, K., Paolo, A., Ireneo, K., Abdallah, D., “Solubility of diamines in supercritical carbon dioxide experimental determination and correlation”,.., 41, 10-19 (2007). (in Chinese)

3 Zhang, J.C., WU, X.Y., CAO, W.L., “Study on critical properties for CO2+cosolvent binary system and ternary system”,...., 10 (2), 223-227 (2002).

4 Tatsuru, S., Naoki, T., Kunio, N., “Solubilities of ethanol, 1-prjopanol, 2-propanol and 1-butanol in supercritical carbon dioxide at 313 K and 333 K”,, 67, 213-226 (1991).

5 Catinca, S., Viorel, F., Dan, G., “Phase behavior for carbon dioxide+ethanol system: experimental measurements and modeling with a cubic equation of state”,.., 47, 109-116 (2008).

6 Hirotoshi, H., Tanimoto, I.Y., “ Phase equilibrium study for the separation of ethanol-water solution using subcritical and supercritical hydrocarbon solvent extraction”,, 84 (1), 297-320 (1993).

7 Wang, W.L., Zhang, X.D., Liu, X.W., “Phase equilibria calculation for supercritical carbon dioxide and alcohol”,...., 24 (4), 1-3 (2003). (in Chinese)

8 Luo, Z.C., Wei,Y. L, Hu, Y., “Phase equilibria study for isopropanol extraction from aqueous solution by using supercritical carbon dioxide”,...., 41 (4), 395-401 (1990). (in Chinese)

9 Tian, Y.L., Han, M., Chen, L., Feng, J., Qin,Y., “Vapor-liquid equilibrium of CO2-ethanol binary system at high pressure”,..., 17 (2), 155-160 (2001).

10 Yun, Z., Shi, M.R., Shi, J., “High pressure vapor-liquid phase equilibrium for carbon dioxide –-butanol and carbon dioxide--butanol”,.., 24 (1), 87-92 (1996).

11 Chen, L., “High pressure equilibrium and critical curves of binary systems containing supercritical CO2”, Ph.D.Thesis, Tianjin University, Tianjin (2004). (in Chinese)

12 Han, B.X., “Mixing supercritical fluid”, Supercritical Fluid Science and Technology, Chinese Petrol Chemical Engineering Press, Beijing (2005). (in Chinese)

13 Bruce, E.P, John, M.P., John, P.O., The Properties of Gases and Liquids, Chemical Industry Press, Beijing, 260-266 (2006). (in Chinese)

14 Chen, Z.X., Gu, F.Y., Hu, W.Y., “Vapor-liquid equilibrium”, The Thermodynamics of Chemical Engineering, Chemical Industry Press, Beijing, 183-187 (2005). (in Chinese)

15 Fleur, B., Jean, P.P., Thierry, C., Roland, T., Jean, F.B., “Modelling solutions of hydrocarbons in dense CO2gas”,...., 21, 1219-1227 (2001).

16 Wang, L.S., “The theory progress of generalized van der Waals partition function”, High Pressure Phase Equilibrium and Transport Property of Fluid, Science Press, Beijing, 75-85 (2002). (in Chinese)

17 John, M.P., Rüdiger, N.L., Edmundo, G.A., “High pressure vapor-liquid equilibrium calculation”, Molecular Thermodynamics of Fluid-Phase Equilibria, Chemical Industry Press, Beijing, 435-441 (2006). (in Chinese)

18 Abolghasem, J., Chan, H.K., Foster, N.R., “Mathematical representation of solute solubility in supercritical carbon dioxide using empirical expression”,.., 24 (1), 19-35 (2002).

19 Zhu, H.G., Tian,Y.L., Chen, L., Qin, Y., Feng, J.J., “High-pressure phase equilibria for binary ethanol system containing supercritical CO2”,...., 9 (3), 322-325 (2001).

20 Wu, J.L., Pan, Q.M., “Prediction of phase behavior for styrene/CO2/ polystyrene mixtures”,...., 10 (6), 706-710 (2002).

21 Yusuke, S., Toshio, I., “Prediction of vapor-liquid equilibria for supercritical alcohol+fatty acid ester systems by SRK equation of state with Wong-Sandler mixing rule based on COSMO theory”,.., 46, 4-9 (2008).

22 Berna, A., Chafer, A., Monton, J.B., Subirats, S., “High-pressure solubility data of system ethanol(1)+catechin (2)+CO2(3)”,.., 20, 157-162 (2001).

2008-12-23,

2009-04-16.

* To whom correspondence should be addressed. E-mail: kxchen@nwu.edu.cn