Heng Zhu(朱恒), Hongchao Shi(施洪潮), Zhengguo Tang(唐政國), and Bing Tang(唐炳)

Department of Physics,Jishou University,Jishou 416000,China

Keywords: topological magnons, magnon-magnon interactions, topological phase transitions, checkerboard ferromagnets

1.Introduction

Over the past two decades,increasing numbers of studies have been devoted to the topological natures of fermion energy band theory in electronic systems,such as graphene.[1,2]Physically, these topological band structures can be detected via the Hall effect, which is in connection with Berry curvatures all over the first Brillouin zone.[3]Until now,the ideas of topological thoughts have been applied to uncharged bosonic systems,e.g.,phonons,[4]polarons,[5]and magnons.[6]In contrast to the Hall effect of electrons, this is not a result of the Lorentz force since magnons carry no electronic charge.Interestingly, the temperature gradient can derive one thermal version of the Hall effect.[7,8]

The magnonic system is viewed as one ideal platform for realizing bosonic analogs of the fermionic phase.Since magnetic properties are readily controlled via the applied magnetic field, magnonic bands can offer a unique platform to explore the rich and still-evolving fundamentals of the energy band theory.In magnetic systems, the emergence of the Dzyaloshinskii-Moriya interaction (DMI) will break the inversion symmetry of the lattice, which can cause a nonvanishing Berry curvature and thermal magnon Hall effects.[9-13]Because(electrically neutral)magnons are not subjected to the Lorentz force,the DMI shall play the role of the effective magnetic field in momentum space by influencing each magnon motion in magnets, which can cause a thermal magnon Hall effect.Experimentally, such thermal magnon Hall effects were first detected in an insulating ferromagnet Lu2V2O7with a pyrochlore lattice structure.[10]Soon afterwards, the thermal magnon Hall effect was theoretically identified in the 2D kagome magnet Cu(1-3, bdc).[14]Moreover, it has also been studied in ferromagnets with other lattice structures, e.g., the honeycomb lattice,[15,16]the Lieb lattice,[17]and the checkerboard lattice.[18,19]

It is worth noting that, in ferromagnets or antiferromagnets, both the Heisenberg exchange coupling interaction and the DMI are in fact nonlinear.Unfortunately,most theoretical studies on topological magnons have been restricted to the linear spin-wave approximation, where magnon-magnon interaction has been ignored.At the low-temperature limit, interaction effects can be deemed to be frozen out.As the temperature increases,the role of the magnon-magnon interaction will become increasingly significant.Recently,the influence of the magnon-magnon interactions on Dirac magnons in 2D honeycomb ferromagnets was first studied by Pershoguba and his coworkers.[20]They have shown that magnon-magnon interaction can cause the remarkable momentum-dependent renormalization of band structures.However, the DMI has been ignored in their work,though it has been experimentally identified in some materials.Later,Mooket al.[21]found that the orientation of the DMI can influence the topological character and the manner of the magnon-magnon interactions in the two-dimensional Heisenberg honeycomb ferromagnet.Furthermore, Luet al.[22]investigated the topological properties of Dirac magnons in a 2D honeycomb ferromagnet by incorporating a second-nearest-neighbor DMI and magnon-magnon interaction into the Heisenberg Hamiltonian of the honeycomb ferromagnet.They showed that the magnon-magnon interactions can induce a topological phase transition of Dirac magnons,which is depicted via the sign transformation of the thermal Hall conductivity.Very recently, Sunet al.[23]have shown that the honeycomb ferromagnetic spin system with a nontrivial DMI can reveal very interesting physics after considering the effect of magnon-magnon interaction.More importantly, they have realized flat bands with nontrivial topology, which can provide one realistic platform to investigate those strongly correlated bosonic systems.

In this article, we will theoretically investigate topological magnons in the Heisenberg ferromagnet on one 2D checkerboard lattice.Inspired by the idea from Ref.[22],the influence of magnon-magnon interaction on magnon band topology shall be analyzed by using the Green function formalism up to the first order in the perturbation theory.Our aim of this work is to study the topological aspect of the checkerboard ferromagnet in the presence of the magnon-magnon interaction.Our results will show that the topological phase transition in 2D checkerboard ferromagnets can be tuned either via the temperature or an external magnetic field, and these transitions are identified via the sign variation of the magnon thermal Hall conductivity.These topological phase transitions induced by the magnon-magnon interaction are accompanied by the gap-closing phenomenon.More details on this work will be fully displayed in the following text.

2.Model

In this research, let us begin with the Heisenberg ferromagnet on the 2D checkerboard lattice.[19,24]Theoretically, the checkerboard lattice can be regarded as one 2D projection of the 3D pyrochlore lattice.Some compounds(such as Sr2F2Se2and Na2Ti2Sb2O)can be described via the checkerboard lattice,[25]and new ferromagnetic materials with checkerboard lattice structures are expected to be synthesized in the future.The Hamiltonian for the checkerboard ferromagnet reads

whereSicorresponds to the localized spin operators.The first two terms are,respectively,first-nearest-neighbor and secondnearest-neighbor (ferromagnetic) exchange coupling interactions (J ＞0 andJ′＞0).The third term denotes the firstnearest-neighbor DMI,whereDi j=νijDezis the DMI vector between sitesiandj.It is noted thatvi j=±1 corresponds to one orientation-dependent constant in analogy with the Kane-Mele model.The last term signifies the coupling to the applied magnetic fieldH=Hzez.For convenience,we seth=gμBHzin the following text.As displayed in Fig.1, there are two inequivalent lattice sites,A and B,in the present 2D checkerboard spin lattice.One can see the ferromagnetic coupling interactionJand the DMIDbetween first-nearest-neighbor magnetic ions at sites A and B.Furthermore, the ferromagnetic exchange coupling interactionJ′is present between the second-nearest-neighbor lattice sites A and A,and B and B.

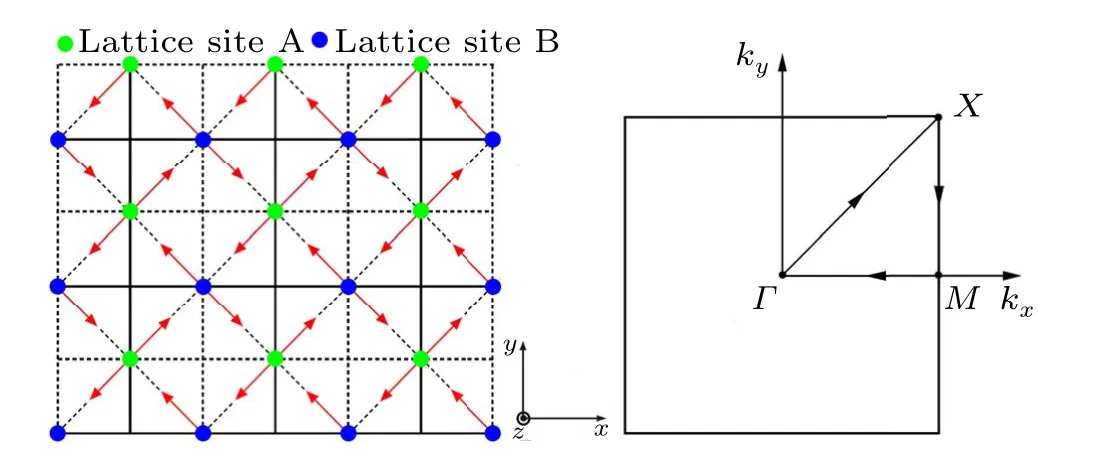
Fig.1.A scheme of the 2D checkerboard lattice(left panel)and its first Brillouin zone (right panel).Both J and D stand for the first-nearestneighbor interactions between localized spins at lattice sites A and B.Here,J′corresponds to the second-nearest-neighbor interactions between lattice sites A and A,and B and B,being along those solid lines.In the right panel,one can see that there is one path connecting the Γ =(0,0),M=(π,0),and X =(π,π)three points.

Here,δnis the vector connection of the nearest neighbors,ζnis the vector connection of the second-nearest neighbors, andvijis absorbed in(-1)n.The matrixH0(k)can also be recast into the following form:

From Eq.(7),we note that the magnon energy spectrums of the present checkerboard ferromagnet contain two different bands, i.e., the optical “up” (upper) and acoustic “down”(lower)bands.In Fig.2(a),we plot the magnon energy dispersion curve of the 2D checkerboard ferromagnet.In the absence of the DMI, i.e.,D=0, the “up” and “down” bands touch at theXpoint.Physically,the DM interaction can destroy the inversion symmetry of the 2D checkerboard ferromagnetic lattice, opening a magnon band gap Δε=8DSat theXpoint.Figure 2(b) displays the density of states per unit cell as one function of energy for two energy bands in Eq.(7).The interesting properties of the present system are manifested near theXpoints.When the magnon band gap opens,the energy band structure is topologically nontrivial and the Chern numbers of two magnon energy bands are nonzero.Until now, both the spin Nernst effect and the magnon thermal Hall effect of the checkerboard ferromagnet have been systematically studied in Refs.[18,19].

Fig.2.(a) Magnonic band structures of the checkerboard ferromagnet along the path Γ-X-M-Γ.(b) The density of states per unit cell of the ferromagnet on the checkerboard lattice.The parameters are chosen as J′=0.1J,h=0.1J,and S=1/2.

3.Interacting topological magnons

3.1.The renormalization of the magnon energy band

By substituting the higher-order expansion of the HP transformation into the original Hamiltonian (1), we can derive the magnon-magnon interacting term?int,which is given by

To properly consider the role of the magnon-magnon interaction,we employ the perturbation technique developed by Sunet al.[23]to obtain the form of the first-order (Hartreetype) self-energy that will yield a renormalized magnon energy spectrum.Using a similar approach,Luet al.[22]obtained the renormalized energy bands of honeycomb ferromagnets.Here,we first write the first-order Dyson equation for interacting magnons,[23]which reads

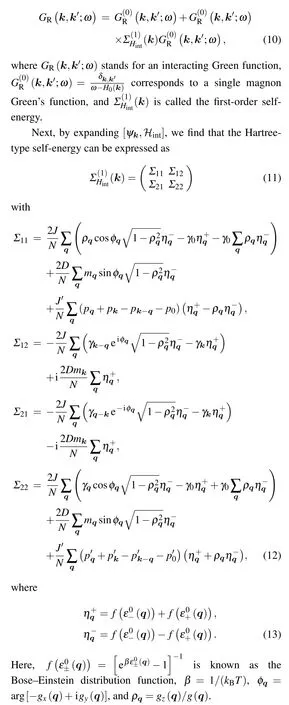
Thus, we can obtain a first-order renormalized Hamiltonian for our system,which has the following form:

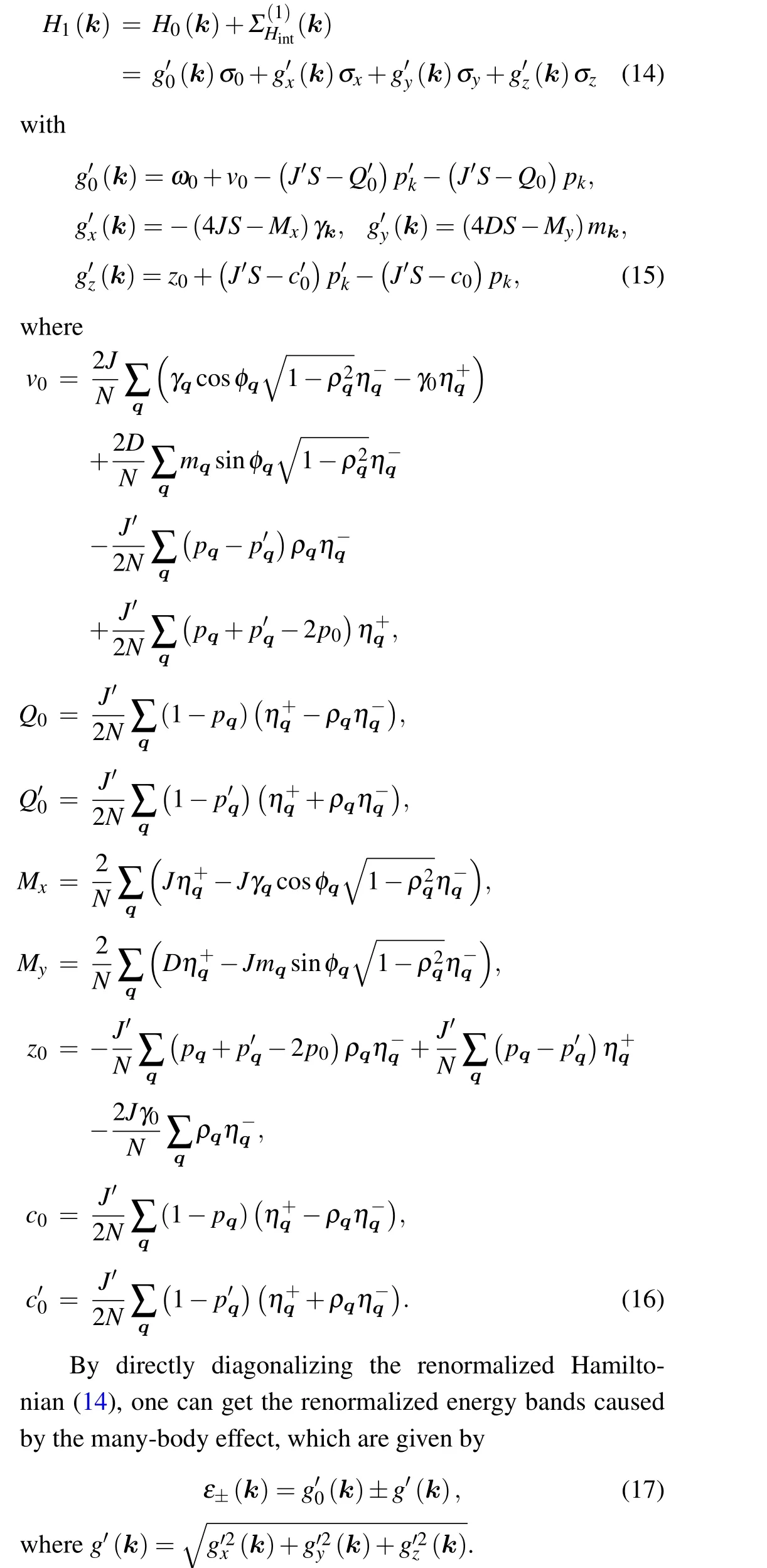
In the low-temperature approximation, the magnonmagnon interaction can be neglected and, at the same time,the self-energy term vanishes.Specifically,the interaction effect is deemed to be frozen out in this approximation.But,as the temperature increases, the effect of the magnon-magnon interaction will become increasingly significant.However,as the temperature increases,the magnon-magnon interaction cannot be abandoned, and then we need to consider the selfenergy.To our knowledge, there are some well-established approaches, such as inelastic neutron scattering,[26,27]inelastic x-ray scattering,[28]and Brillouin light scattering,[29-31]to experimentally detect the renormalized magnon energy band.

Figure 3 displays the renormalized magnon band structures of the checkerboard ferromagnet for different values of the temperatureT.One can clearly see that,with the increase in the temperature, the renormalized magnon band gap decreases,and the spectrum becomes gapless at the pointXdecreases and will close atT ≈2.18Jfor a certain value ofh.Once one further increases the value ofT, the gap will reopen and its width increases with the temperature.Moreover,whenT ≈2.69J,the gap-closing phenomenon also appears at the pointMfor this particularh.To understand the influence of the magnetic field intensity on the width of the band gap,we plot band gaps at the pointsXandMas one function of temperature corresponding to different values ofh,which are shown in Fig.4.One can clearly see that the critical temperature(TX,cfor the pointX,andTM,cfor the pointM)for the gap closing increases as the value ofhincreases.For the sameh,TM,cis greater thanTX,c.

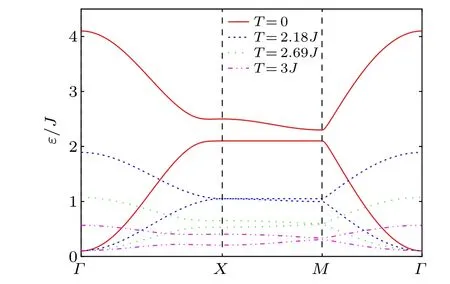
Fig.3.The renormalized magnon band structures for four different temperatures along the path Γ-X-M-Γ.The parameters are set to J′=0.1J,D=0.1J,h=0.1J,and S=1/2.

Fig.4.The gaps as a function of temperature(a)at the point X;(b)at the point M.The parameters are chosen as J′=0.1J,D=0.1J,and S=1/2.

3.2.Topological properties of interacting magnons

In magnetic systems, the existence of the DMI breaks the inversion symmetry of the lattice, which can give rise to the nontrivial band topology.Physically, this nontrivial band topology is described via a nonvanishing Berry curvature.In the present 2D magnon systems, the Berry curvature has the following form:

It is not hard to findC+=-C-.Here, we will achieve the topological phase transition in the upper band fromC+=1 toC+=-1(orC+=-1 toC+=-1).

Figure 5 displays the Chern number of the renormalized magnon band as one function of temperatureT.It is clearly seen that the system can reveal two topological phases,namely,(C+,C-)=(-1,1)and(C+,C-)=(1,-1).Based on the previous results,we realize that the renormalized magnon gap can close and reopen at the critical temperaturesTX,candTM,c, which signifies that two topological phase transitions may exist atTX,candTM,c,respectively.

Fig.5.The Chern number for the renormalized magnon band versus the temperature T: (a)the upper band, (b)the lower band.The relevant parameters are fixed as J′=0.1J,D=0.1J,h=0.1J,and S=1/2.

In these two-dimensional ferromagnets, the longitudinal temperature gradient can cause one transverse heat current via the Berry curvature.Theoretically, such formation of the transverse heat current is called the magnon thermal Hall effect.[7,32]The magnon thermal Hall conductivity can be defined via

In the linear limit, namely, ignoring magnon-magnon interactions,κxyis always greater than zero, as shown in Ref.[19].When the magnon-magnon interaction is considered,the topological phase transition will occur.In Fig.6,we show the dependence ofκxyon the temperatureT.We can clearly see thatκxychanges continuously as the temperature increases, and is positive forT ∈[0,TX,c)∪(TM,c,∞)while it is negative forT ∈(TX,c,TM,c).Evidently,the magnon thermal hall conductivity and Chern number of the upper band possess the same signs as the increasing temperature.In principle,the sign reversal of the thermal Hall conductivity is one vital indicator of the topological phase transition.In Fig.6, one can clearly see that the topological phase transition occurs twice as the temperature increases.This result is very interesting.Moreover, it is clearly seen that the critical temperature for the occurrence of one topological phase transition rises as the magnetic field strength increases.

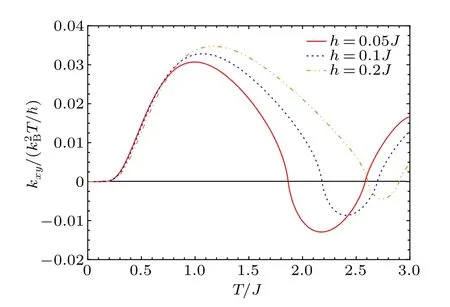
Fig.6.The thermal Hall conductivity versus temperature for various values of h.The other parameters are set to J′=0.1J,D=0.1J,and S=1/2.

4.Conclusion

To conclude, after adding the first-order (Hartree-type)self-energy linked to the magnon-magnon interaction into the single-magnon Hamiltonian, the system will have two different topological phases: (C+,C-)=(1,-1) and (C+,C-)=(-1,1).It has been shown that the topological phase can be controlled either via the temperature or the applied magnetic field due to magnon-magnon interactions.In particular,we have found that the topological phase transition can occur twice with the increase in the temperature,which is a new finding.In addition,our results have shown that the magnon thermal hall conductivity and the Chern number of the upper band possess the same signs as the increasing temperature.Thus the sign reversal of the magnon thermal Hall conductivity can be viewed as a vital indicator of a topological phase transition of the checkerboard ferromagnet.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No.12064011), the Natural Science Fund Project of Hunan Province(Grant No.2020JJ4498),and the Graduate Research Innovation Foundation of Jishou University(Grant No.Jdy21030).We would like to thank Dr.Hao Sun for many useful suggestions.