Mengwei Sun , Jian Liu ,,, Lu Ren , and Changyin Sun , Senior,

Dear Editor,

This letter examines the fixed-time stability of the Nash equilibrium (NE) in non-cooperative games.We propose a consensus-based NE seeking algorithm for situations where players do not have perfect information and communicate via a topology graph.The proposed algorithm can achieve NE in a fixed time that does not depend on initial conditions and can be adjusted in advance.In this strategy,players use their estimates of other players’ actions to update their own actions.We present sufficient conditions that ensure the fixedtime stability of the NE through rigorous Lyapunov stability analysis.Finally, we provide an example to verify the feasibility of the theoretical result.

Game theoretic methods have become prevalent in engineering applications, such as power allocation [1], cooperative control [2],[3], energy consumption control [4], and self-driving [5].Once a specific problem has been modeled as a game, the question becomes how to find the NE.In a game, each player aims to find a strategy that minimizes its own cost function.The NE of a game is a set of actions for which players can no longer decrease their cost functions by solely changing their own actions.In [1], the zero-sum game of two networks of agents was investigated.The potential game and aggregate game were considered in [2] and [4], respectively.For more generalized non-cooperative games, an extreme seeking based method was developed in [6], but it required global information,which may not be applicable to practical problems.To tackle this issue, researchers have paid attention to studying NE seeking strategies under imperfect information.In [7], a gossip-based algorithm was designed for discrete-time NE seeking.In [8], the authors proposed a continuous-time NE seeking algorithm that incorporates a consensus protocol [9]-[14].A passivity-based approach was developed in [15] for nonlinear and heterogeneous players.The papers[16]-[18] studied NE seeking under disturbance, control input saturation, and switching topologies, respectively.

The convergence rate is an important index for evaluating system performance.While the aforementioned results all achieved NE with an asymptotic convergence rate, where the fastest rate is exponential,the infinite convergence time usually does not meet the requirement of practical systems.To acquire NE more quickly, Fanget al.[19]proposed two finite-time NE seeking algorithms that employ signum and saturation functions.However, the convergence time of the finite-time result is related to the initial conditions, which are not always available in practice.To overcome this disadvantage, the authors of [20] proposed a fixed-time NE seeking algorithm based on extreme seeking.The prescribed-time algorithms were developed based on the motion-planning method in [21] and the time base generator in [22].

Inspired by the fixed-time leader-following consensus protocol in[13], a new algorithm for fixed-time NE seeking under a communication graph is proposed by integrating leader-following consensus and gradient play in this letter.It is not a trivial extension, and difficulties arise from two aspects.Firstly, in the fixed-time leader-following consensus problem, the leader’s input is commonly assumed to be bounded.In the consensus-based NE seeking algorithm, the action update law is considered the leader’s input.However, to achieve fixed-time NE seeking, the action update law cannot be bounded.Secondly, the traditional quadratic form of the Lyapunov function is not applicable.The nonlinearity of the gradient play exists in the action update law, making the stability analysis more difficult.

The contributions of this letter are summarized as follows.First,the proposed method extends the asymptotic consensus-based NE seeking strategies [8], [16], [18] to achieve a fixed-time convergence result.A new Lyapunov function is designed to prove fixed-time convergence.Moreover, it is a distinct method from that presented in[20].The explicit form of the settling time is given, which is independent of the initial conditions and only relies on the design parameters, allowing it to be predetermined prior to system operation.Second, in contrast to the NE seeking strategy studied in [22], which steers actions to a neighborhood of the NE with size dependent on the initial conditions, the proposed algorithm in this letter attains the exact NE.

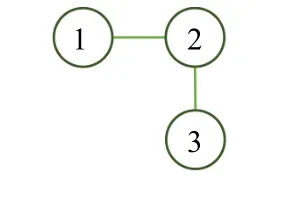
Fig.1.Communication topology between the three players.

Fig.2 displays the evolution of the players’ actions under the proposed fixed-time NE seeking algorithm, which obtains the NE in 7 s.Fig.3 illustrates the players’ estimates of the actions, with the estimated values rapidly converging to the actual actions.

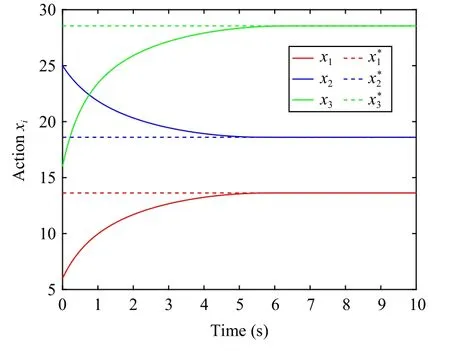
Fig.2.Plot of the actions of players.

Fig.3.Plot of the players’ estimates on actions.

Conclusion: This letter investigates the fixed-time stability of the NE in networked games and provides an upper bound for the settling time.Future work can extend the proposed NE seeking algorithm to achieve prescribed-time convergence, realize fully distributed control, incorporate an event-triggered mechanism, or tackle practical situations such as switching topologies, external disturbances, and players with higher-order dynamics.It can also be adapted to solve different types of games, such as aggregative games and multi-cluster games.

Acknowledgments: This work was supported by the National Natural Science Foundation of China (62373107, 61921004, 62303009),the Natural Science Foundation of Jiangsu Province of China(BK20202006), and the “Zhishan” Scholars Programs of Southeast University.