Zhiqiang Sun(孫志強(qiáng)), Guolin Hou(侯國(guó)林), Yanfen Qiao(喬艷芬), and Jincun Liu(劉金存)

School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China

Keywords: Hamiltonian system,symplectic elasticity,quasicrystals,analytic solution,state function

1.Introduction

Quasicrystals (QCs) are a kind of solid intermediate between crystal and amorphous materials, which were first discovered by Shechtmanet al.[1]The unique quasi-periodic structure makes QCs become a new kind of functional materials and structural materials.[2,3]

QCs have many excellent properties, such as high strength, abrasion resistance, hardness, thermal conductivity,and low adhesion.[4,5]It should be noted that the properties of QCs are affected by defects such as dislocations,cracks,holes,and inclusions.[6–12]Many methods and techniques have been developed to address the problems of elasticity and defects in QCs.Among them, symplectic elasticity approach,[13–15]the pseudo-Stroh formalism method,[16,17]the state-space method,[18,19]the integral transformation method,[20]the differential quadrature method,[21,22]the complex variable function method,[23–26]and the state-space based differential quadrature method[27]are practical to construct the analytical or numerical solutions of QCs.The integral transformation and differential quadrature methods are numerical and have been approved to be highly efficient for the rapid solution.The state-space-based differential quadrature method[27]inherits the advantages of the state-space method and the differential quadrature method.Its convergence speed is fast and can apply to different boundary conditions.However,the state-space method must be revised to solve the clamped-supported and mixed boundary conditions.The complex variable function method often leads to high-order partial differential equations,which puts forward higher requirements for the smoothness of solutions and may be difficultly solved further by separating variables.[23]The symplectic elasticity approach is the method of separating variables based on the Hamiltonian system.It can construct the general solution of the considered problem without any assumptions about the solution forms.According to the Vainberg theorem[28]in variational theory,a symmetric differential system can continually be transformed into a suitable Hamiltonian system, which provides the possibility for applications of the symplectic elasticity approach in elasticity mechanical problems because the considered mechanical equations are primarily symmetric.Recently, the symplectic elasticity approach has been applied to establish the final governing equation of Laue class 15,[14]which provides a feasible idea for solving some complex quasicrystal problems.

This paper aims to extend the symplectic elasticity approach to solve the inhomogeneous dodecagonal QC plates.In the geometry of symplectic space, the phonon stress, phason stress, and displacements are set as unknown functions and included in the state vector, and then the formed first-order differential system,a Hamiltonian system,is introduced.Additionally, using the symplectic orthogonality relations of the eigenvectors,the general solutions of phonon and phason displacement under the given boundary conditions are obtained.Finally, the accuracy of the symplectic elasticity approach is verified by numerical examples of QC plates under uniform and concentrated loads, and the effects of different phason elastic constants on displacements and stresses are analyzed.The numerical results show that the symplectic elasticity approach is an effective tool for analyzing the mechanical behavior of QC plates.The presented method in the current paper can also be used to solve other boundary conditions.

2.Hamiltonian system of dodecagonal QCs

According to the linear elastic theory of QCs, the basic equations for the inhomogeneous plane elasticity problem of dodecagonal QCs are described in the following.[29]The equilibrium equations are

and generalized Hooke’s laws have the following form:

whereux,uyandwx,wydenote the phonon displacements and phason displacements;σxx,σxy,σyx, andσyyare the phonon stresses;Hxx,Hxy,Hyx,andHyyare the phason stresses;q1,q2,q3, andq4are the body forces;L,M,K1,K2, andK3are the elastic constants.For simplicity,K1+K2+K3is abbreviated toK4.

To establish the Hamiltonian system,define the displacement vector as

where the superscript T represents the transpose.The strain energy densityU(q, ˙q)can be expressed as

where ˙()≡?/?y.Moreover,we introduce the Lagrange density function as

Consider a dodecagonal QC rectangular domain with lengthl(0≤y ≤l)and widthh(0≤x ≤h).To build the variational operation,the equilibrium Eqs.(1a)–(1d) can be obtained by taking the variation with respect toux,uy,wx,andwy,respectively.Applying the Legendre transformation, the corresponding dual vector is given as follows:

According to Eqs.(3)and(6),defining a state vector

the Hamiltonian system can be expressed as

where the Hamiltonian operator reads

f(x,y)=?(q3,q4,q1,q2,0,0,0,0)Tis an inhomogeneous term related to body forces.Moreover, we consider Eq.(8)to satisfy the following boundary conditions shown in Fig.1,

Remark 1 The Hamiltonian system (8) derived here is also applicable to other complex boundary conditions,such as clamped or free.The solution to those problems may require the use of the symplectic superposition methods,[30,31]which are not covered in this study.

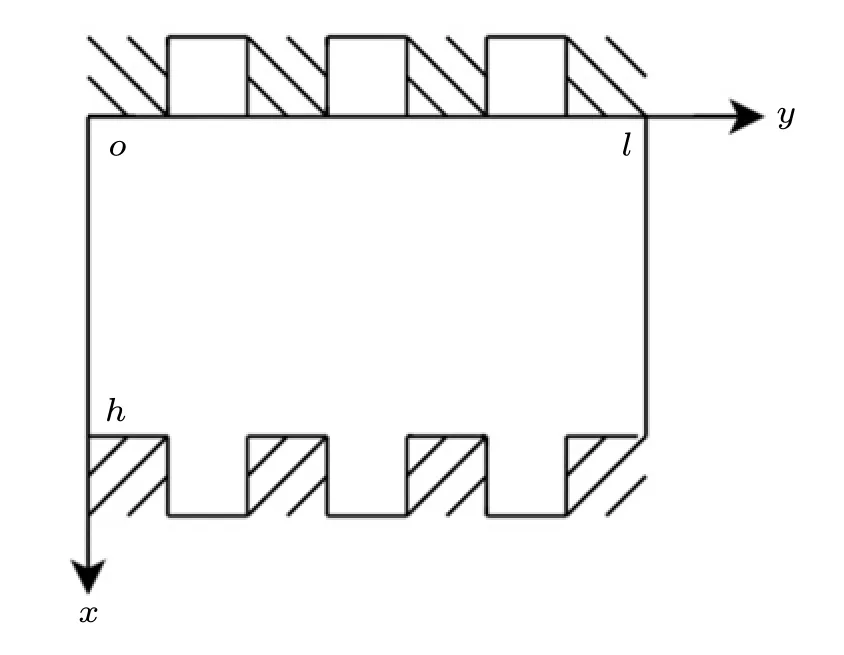
Fig.1.Geometry of boundary conditions(10).

3.Eigenvalues and eigenvectors of H

According to the theory of linear differential equations,we should first solve the following homogeneous form of Eq.(8):

Equation (11) can be solved by the method of separating variables.[32]Assuming

and substituting it into Eq.(11),we arrive at

whereψ(y)is easy to get,andΦ(x)is an unknown eignvector corresponding to the unknown eigenvalueμ.The eigenvalue problem

with the boundary condition (10) is needed to take a lot of effort to solve.According to Eq.(10),we find that the eigenvector has the following form:

whereαandAi(i=1,2,...,8)are unknown constants which depend onμand can be calculated from Eq.(14).

Combining Eqs.(10)and(14),the characteristic polynomial is derived as follows:

From Eq.(15),we obtain the eigenvaluesμn=αn=±nπ/h,μ?n=?μn(n= 1,2,...), and corresponding eigenvectors with respect toμnare given by

Similarly,the basic eigenvectors ofμ?n=?μn(n=1,2,...)are

and first-order Jordan form eigenvectors ofμ?n=?μn(n=1,2,...)are

Additionally,μ=0 is also a multiple eigenvalue ofH.The eigenvectors ofHwith respect to eigenvalueμ=0 include basic eigenvectors

and first-order Jordan form eigenvectors

4.Symplectic orthogonality and completeness

The symplectic orthogonality of the generalized eigenvectors of the Hamiltonian operatorHis analyzed first since it plays an important role in representing the solution of the Hamiltonian system.[32]

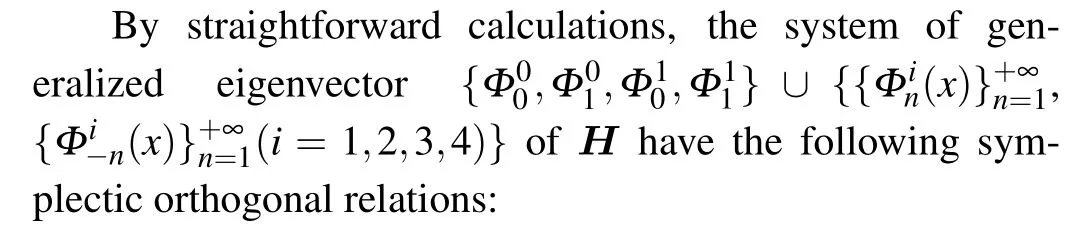
In addition,we have

The following theorem is one of the main results in this paper, which characterizes the completeness of the generalized eigenvector system ofHand also ensures the feasibility of separating variables in the Hamiltonian system.It is worth noting that all of the calculations in this section can be easily achieved by symbolic software like Mathematica.

Proof According to the symplectic orthogonal relationship(16)and(17),we take

Thus,we have

where the eight components in the above expression are the Fourier series expansions of functionsfi(x) (i= 1,2,...,8)under the orthogonal systemorin Hilbert spaceL2(0,h).Accordingly,

is valid,and the proof is completed.

5.Analytic solution of the original problem

According to Theorem 1 and the principle of superposition of solutions, the general solution of Eq.(8)can be given in the form

Let the Fourier expansion of the inhomogeneous termf(x,y)=(q4,q3,q1,q2,0,0,0,0)Tin Eq.(8)be

where

The details of(i= 1,2,3,4) are expressed in Appendix A.

Substituting Eqs.(18)and(19)into Eq.(8),and by simple calculations,we obtain

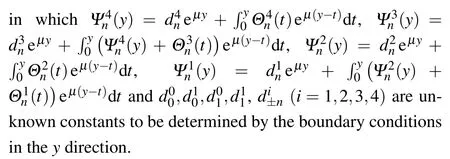
According to the form of the state vectorU(x,y),the analytic solutions ofHxy,Hyy,σxy,σyy,wx,wy,ux, anduycan be obtained by taking the first component through the eighth component of Eq.(20).For the sake of brevity,we do not write out their specific expressions.

6.Numerical examples

This section presents the behavior of solutions of the QC plates under the concentrated load,uniform load,and mechanical load based on the symplectic analytical solution obtained in Section 5.To this end,we consider the following boundary conditions in they-direction:

For convenience of numerical simulation,we assume that the body forcesq1=q2=q3=q4.Due to the lack of comparative data, we introduce the FITM for the displacementsux,uy,wx,andwyto show the validity of the symplectic elasticity approach.The expressions of phonon and phason displacements given by the FITM can be found in Appendix B.The material constantsL=0.5741 GPa,M=0.88445 GPa,K1=1.22 GPa,K2=0.24 GPa, andK3=0.6 GPa are taken as those in Ref.[13].

6.1.Concentrated load and uniformly distributed load

The central concentrated loadq1=q2=q3=q4=Pδ(x ?x0,y ?y0) is examined at the (x0,y0)=(h/2,l/2)of plate,wherePis the intensity,andδ(·,·)denotes the wellknown Dirac function.As the ratio of length and width varies,the results of numerical tests under central concentrated load are shown in Tables 1 and 2 for the displacement responses at fixed horizontal coordinates (x,y)=(h/4,l/4) and (x,y)=(h/4,h/4),respectively.The uniformly distributed load of intensityqis examined, and the numerical results are given in Table 3.

Table 1 shows that the symplectic elasticity approach performs better than the FITM since it gets a reasonable convergence rate with only 20 terms.Also,we use the first 20 terms of Eq.(20)to show the phonon and phason displacements with different length–width ratios(1≤l/h ≤2)in Fig.2.

As shown in Fig.2, the tendency of change in displacements with a change in aspect length–width ratios of the QCs plate is different for the responses at two fixed horizontal coordinates.For the fixed valueh,the changes ofuxandwx(uyandwy)at(h/4,l/4)are increasing(decreasing)aslgoes up.This trend depends on the influences of boundary conditions (10)and (21), and the variations of distance between (h/4,l/4)and (h/2,l/2).However, the responsesux,wx,uyandwyat the fixed point (h/4,h/4) are decreasing aslbecomes larger because of the influence of boundary conditions is unchanged,and the effect of the load is gradually weakening.

In addition,whenh=l,we have the phason displacementux=uyand the phonon displacementwx=wyfor the centralized load, which is in agreement with the case for uniformly distributed load.

Fig.2.The phonon and phason displacements of the QC plate under a centrally concentrated load: (a) the response at (x,y)=(h/4,l/4),(b)the response at(x,y)=(h/4,h/4).

Table 1.The calculation results under central concentrated load(x,y)=(h/4,l/4).

Table 2.Calculation results under central concentrated load(x,y)=(h/4,h/4).

6.2.Mechanical load

In this subsection we analyze the effect of the phason elastic constants on the displacements and stresses.In the absence of body forces,we assume that the right side of the QC plate is subjected to the phonon and phason mechanical loads,i.e.,

whereH0andσ0are the amplitude of the loading.Meanwhile,all other components on the left and right sides of the plate are zero.Consequently, the boundary conditions along theydirection are

wherepandqare expressed in Eqs.(3)and(6),respectively.

Following the previous work,[33]we takeH0=σ0=1 N/m2,α=π/h, the dimensions of the plate areh×l=0.3 m×0.3 m,and consider the responses wheny=0.75l.

Based on the above loads, we analyze the effect of the phase elastic constantsKi(i=1,2,3)on some physical components in the QC plates.We let the phason elastic constants beKi,0.5Ki,0.1Ki(i=1,2,3),and the results of the calculations are shown in Fig.3.It can be seen that the magnitudes of the phason displacementswxandwydecrease with decreasing value of phason elastic constantsKi(i=1,2,3)[see Figs.3(c)and 3(d)], while there is no effect on the trends of the phason and phonon stresses components[see Figs.3(a)and 3(b)].Specifically, the phason displacements are more sensitive to the phason elastic constants than the phason and phonon stress.

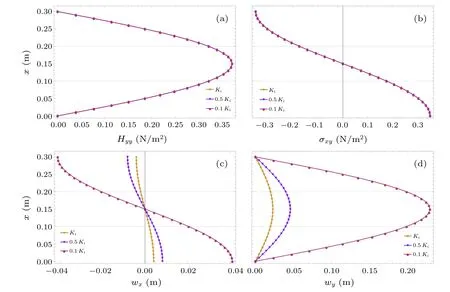
Fig.3.Displacements and stresses with different phason elastic constants: (a) phason stress Hyy, (b) phonon stress σxy, (c) phason displacement wx,and(d)phason displacement wy.

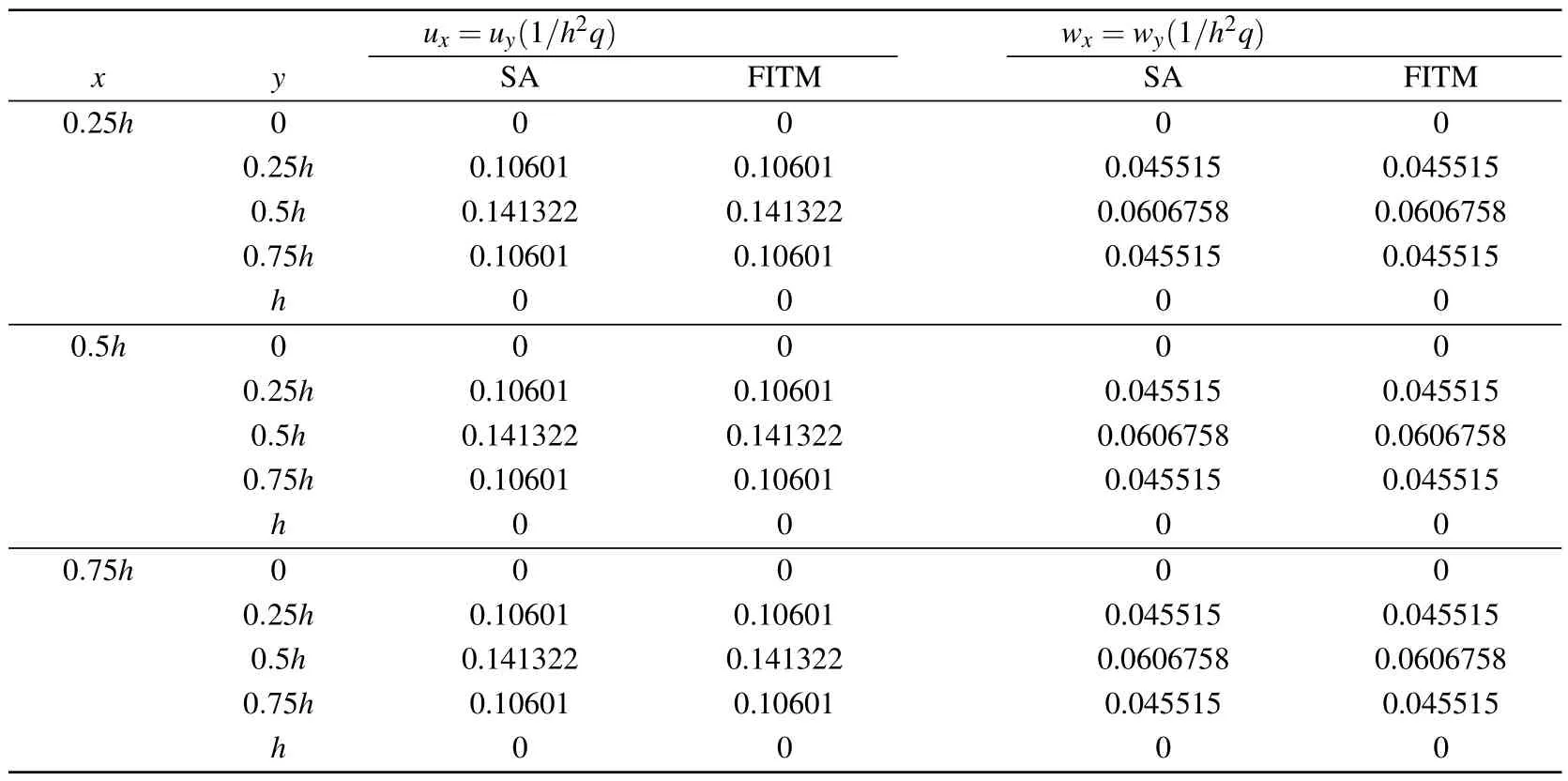
Table 3.Calculation results under uniform load.

7.Conclusions

In summary, we have solved QC equations by employing the symplectic elasticity approach.By introducing a generalized displacement vector, the Hamiltonian system of dodecagonal QCs is derived from the strain energy density and Legendre transformation.Then, the symplectic elasticity approach is adopted to get the general solutions of the Hamiltonian system.It is worth noting that the 1st, 2nd, 3rd, and 4th components of the general solution (20) are the phonon and phason stresses,and the 5th,6th,7th,and 8th components of (20) are the phonon and phason displacements.The displacements and stresses responses of QC plates under the concentrated,uniformly distributed,and mechanical loads are discussed in detail.For the case of concentrated load,the trends of responses at the fixed point and moving point are different from the changes in length–width ratios.The numerical examples of the mechanical load show that the magnitude of the phason displacements decreases with decreasing value of phason elastic constants.The comparison data are constructed by FITM,which justifies calculating of the symplectic elasticity approach.The approach is direct and rational,providing a systematic step to solve the related problems of QCs.

Appendix A

Appendix B

Substituting Eqs.(2a)–(2g)into Eqs.(1a)–(1d),we obtain

where ?2=?2/?x2+?2/?y2.

Based on boundary conditions(10)and(21),we can define eight double finite integral transforms with respect towx,wy,ux,uy,q1,q2,q3,andq4as follows:

whereαm=mπ/handβn=nπ/l(m,n=1,2,3,...).

The inverse transforms are given by

By simple calculations, Eq.(B1) is transformed into the following form:

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.12261064 and 11861048), the Natural Science Foundation of Inner Mongolia,China(Grant Nos.2021MS01004 and 2022QN01008), and the High-level Talents Scientific Research Start-up Foundation of Inner Mongolia University(Grant No.10000-21311201/165).