戴韞卓 ,吳瀟然 ,葉榮兵 ,趙子楠 ,胡日成 ,張榮茂

(1.浙江省自然資源網(wǎng)上交易中心,浙江杭州 310007;2.浙江大學(xué)數(shù)學(xué)科學(xué)學(xué)院,浙江杭州 310058)

§1 引言

土地價格在國民經(jīng)濟體系中扮演著重要作用,它不僅是土地要素參與宏觀調(diào)控的經(jīng)濟杠桿[1],同時也是評估宏觀經(jīng)濟的重要指標[2].如何有效地分析地價的變動規(guī)律,對于我國土地市場健康有序的發(fā)展將具有十分重要的意義.

地價指數(shù)是衡量土地價格隨時間變化的趨勢與幅度的指標,反映一個城市各類土地價格變化及其總體綜合平均變化趨勢.有效構(gòu)建地價指數(shù)的統(tǒng)計模型與實時動態(tài)預(yù)測,是推進自然資源要素配置,優(yōu)化市場環(huán)境,降低交易成本,加強內(nèi)部監(jiān)管,強化社會監(jiān)督,促進廉政建設(shè)的有效保證.

然而,由于地價自身的特性:(a) 數(shù)據(jù)不可重復(fù)性(同一塊地往往只一個交易價格);(b) 非平穩(wěn)特性(價格與地理位置緊密相關(guān)),導(dǎo)致數(shù)據(jù)之間的結(jié)構(gòu)往往具有較大的差異,而具有相近結(jié)構(gòu)的數(shù)據(jù)量往往很少,使得價格指數(shù)的統(tǒng)計建模特別困難,見[3-4].目前,國內(nèi)對地價指數(shù)統(tǒng)計建模的理論研究較少.業(yè)界大多使用加權(quán)平均的簡單方法進行計算,見[5-9],這樣的指數(shù)往往無法有效地反映地價的非平穩(wěn)特性和動態(tài)變化,難以被用于預(yù)測.

地價往往隨著時間的變化,所處的區(qū)域不同,外界環(huán)境因素影響呈現(xiàn)空間和時間上的動態(tài)變化.在時域上,同一時間拍賣的土地受相同的市場大環(huán)境,政策影響,其成交價格相關(guān)性也更強.在空間上,相鄰地塊共同的周邊環(huán)境與配套決定了他們的價格也有所相關(guān).至于外界因素,影響地價的外部因素不勝枚舉,很大一部分因素與地塊空間位置相關(guān),如路網(wǎng)稠密程度,公共交通站點個數(shù),自然景觀數(shù)量,與商務(wù)生活中心的距離等.此外,地價還受到用地類型,容積率等與空間位置無關(guān)的外生變量的影響.

為了捕捉地價在時空上的動態(tài)信息,同時考慮外生變量對其影響,本文提出一類帶外生變量空間自回歸的地價建模方法,該方法通過提取同一時期內(nèi)地價指數(shù)的共同趨勢來刻畫地價指數(shù),并基于自回歸時間序列實現(xiàn)了地價指數(shù)的趨勢預(yù)測.筆者也將所提的空間自回歸模型和自回歸時間序列應(yīng)用于浙江省土地招拍掛數(shù)據(jù),并通過該數(shù)據(jù)來說明具體實施過程及預(yù)測效果.從實驗的結(jié)果可以看出,所提出的模型符合過往的經(jīng)驗及市場判斷,具有較好的擬合度.

§2介紹地價指數(shù)的空間自回歸建模;§3節(jié)介紹空間自回歸模型在浙江省地價指數(shù)上的應(yīng)用;§4總結(jié)本文所做的工作及今后的展望.

§2 模型

2.1 空間自回歸模型及其參數(shù)估計

同一時期的土地招拍掛成交數(shù)據(jù),其畝均成交單價很大程度上依賴于地塊所處地理位置,在空間中產(chǎn)生聚集效應(yīng).例如,相比于郊區(qū)土地,市中心附近的出讓地塊將具有更高的價格水平.為了捕捉土地成交價格在空間上的相依性,本文使用空間自回歸模型(Spatial Autoregressive Model,即SAR)見[10],對同一時期內(nèi)土地交易數(shù)據(jù)進行建模.SAR模型被廣泛應(yīng)用于空間數(shù)據(jù)的統(tǒng)計建模,其表達形式為

其中y為所研究區(qū)域的因變量,W為權(quán)重矩陣,X為外生變量構(gòu)成的設(shè)計矩陣,?為噪聲項,ρ和β為模型的待估參數(shù).對于擬合SAR模型,一個關(guān)鍵的步驟便是參數(shù)估計,本文采用極大似然估計方法,首先令A(yù)=I-ρW,可以將模型簡化為

其中?是獨立標準正態(tài)噪聲項.該模型可以看作關(guān)于參數(shù)的非線性模型f(y,X,θ)=?,其中θ=(ρ,β′)′是未知參數(shù)向量,f是廣義非線性泛函.盡管噪聲項?有著良好的聯(lián)合分布,但其不可觀測的性質(zhì)導(dǎo)致必須通過y構(gòu)造似然函數(shù),進而需要引入將?轉(zhuǎn)化為y的Jacob行列式

接下來便可基于噪聲項的聯(lián)合正態(tài)性加之Jacob行列式得到觀測值y的對數(shù)似然函數(shù)

從上式可以看出,最大化似然函數(shù)L相當(dāng)于最小化Jacob修正后的偏差平方和,Jacob行列式|A|中的空間項使其不同于普通最小二乘估計,所以需要保證|A|>0,即|I-ρW|>0.進一步,進行極大似然估計需要對待估參數(shù)求解一階偏導(dǎo)數(shù)并令其等于0得到參數(shù)估計值

使用數(shù)值方法求解上述非線性方程組,即可得到參數(shù)ρ與β的極大似然估計.

2.2 地價指數(shù)建模

為保證同一時期內(nèi)數(shù)據(jù)量充足,本文按季度劃分土地交易數(shù)據(jù).對于土地成交價格數(shù)據(jù),其空間聚集效應(yīng)體現(xiàn)在權(quán)重矩陣W上.此外,地塊價格受用地類型影響較大,如住宅用地單價往往高于工業(yè)用地與商服用地,也受土地規(guī)劃的容積率影響,容積率決定地價成本與土地開發(fā)商最終回報的比例.因此建模中將容積率上限與用地類型作為外生變量加入設(shè)計矩陣X,得到按季度劃分的空間自回歸模型

其中yt為pt×1維向量,代表第t期內(nèi)的pt個出讓地塊的畝均成交單價.Ut=(μt,μt,···,μt)為模型的共同截距項,FAR為政府規(guī)劃的該地塊容積率上限,D為以用地類型分類標準的啞變量.

權(quán)重矩陣W的選取使用KNN (k-最近鄰) 原則,確定每個數(shù)據(jù)點固圍非零權(quán)重的個數(shù).選取

其中#Yt表示第t個季度樣本的數(shù)量.接著,計算每個點i和周圍最近k個點的距離dij,j ∈KNN(i),取權(quán)重為

然后使用上一節(jié)所述方法估計待估參數(shù).

由于權(quán)重矩陣W的估計需要用到地塊的地理位置信息,對于少量無坐標數(shù)據(jù)和坐標錯誤的數(shù)據(jù),使用普通最小二乘法建立線性回歸模型

對于上述空間自回歸模型,空間自回歸項與外生變量為每個樣本的異質(zhì)部分,而Ut=(μt,μt,···,μt)為同一季度內(nèi)所有樣本的共同趨勢項,因此獲得每個季度內(nèi)的模型及其參數(shù)值后,選取共同截距項μt衡量地價指數(shù),反映市場行情的變化情況.以第一季度數(shù)據(jù)(t=1)為基準期,并對地價指數(shù)進行位置與尺度放縮,此操作不改變序列的趨勢,但使其落入通常市場認可的指數(shù)區(qū)間.由此可以得到第t季度的地價指數(shù)indext為

由上述步驟得到的指數(shù)序列indext是一個季度時間序列,其ACF圖呈現(xiàn)短記記憶性.因此本文考慮使用自回歸模型(Autoregressive Model,即AR)進行預(yù)測,AR模型的定階可使用AIC,BIC等信息準則,當(dāng)樣本量較小時,信息準則定階效果較差.本文基于土地市場的經(jīng)驗數(shù)據(jù),用之前四個季度的數(shù)據(jù)預(yù)測本期,對指數(shù)建立AR(4)模型并進行點預(yù)測和區(qū)間預(yù)測.

§3 浙江省地價指數(shù)建模與分析

本文使用的數(shù)據(jù)為浙江省自然資源廳提供的時間跨度為2017年10月至2022年11月的浙江省各地市土拍數(shù)據(jù),共計兩萬余條,每條數(shù)據(jù)包含一塊出讓土地的成交單價,成交時間,用地類型,容積率范圍,土地所屬行政區(qū)域與地塊中心經(jīng)緯度等指標.2018年10月以前數(shù)據(jù)大部分缺失經(jīng)緯度信息,另有少量數(shù)據(jù)存在經(jīng)緯度錄入錯誤,對于該部分數(shù)據(jù)在提取截距趨勢項時采用普通最小二乘法估計.

以寧波市數(shù)據(jù)為例,土地的畝均單價在空間上與隨時間分布的圖像如圖1所示,可以看出土地價格在空間與時間上都呈現(xiàn)出非平穩(wěn)的特性.

圖1 寧波市土地拍賣價格的時空分布圖

2.3 地價指數(shù)趨勢擬合

根據(jù)§2的建模步驟,按季度劃分土地成交數(shù)據(jù),在每個季度內(nèi)對帶土地坐標的數(shù)據(jù)進行SAR模型建模,可以得到各季度內(nèi)參數(shù)估計結(jié)果.以杭州市商品房數(shù)據(jù)為例,由于前四季度數(shù)據(jù)坐標信息缺失,僅使用普通最小二乘回歸,從第五季度開始(即2018年第四季度起),各季度SAR模型參數(shù)估計結(jié)果見表1.

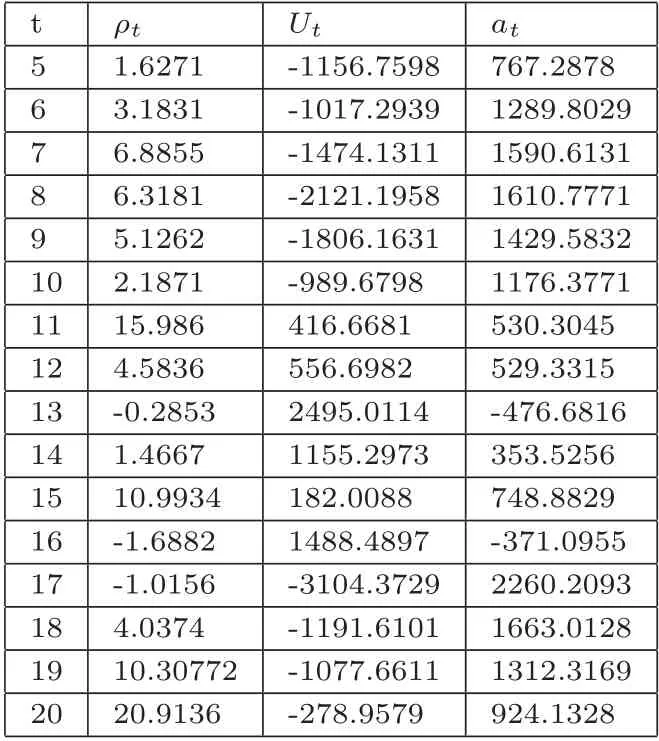
表1 杭州市商品房地價指數(shù)模型參數(shù)估計

得到SAR模型參數(shù)估計后,提取季度內(nèi)共同趨勢項Ut,進行量綱處理后得到地價指數(shù)的擬合曲線,本文分別處理了浙江全省數(shù)據(jù),杭州市與寧波市兩個副省級城市數(shù)據(jù).全省數(shù)據(jù)共有67種用地類型,其中商品房,工業(yè)用地與商務(wù)金融用地三種類型的成交土地最多,關(guān)注度也最高.不同用地類型的地價指數(shù)趨勢不盡相同,以寧波市數(shù)據(jù)為例,如圖2所示,商品房的平均成交單價高于其他用地類型,由于市場也最為關(guān)注商品房土地的價格走勢,接下來的數(shù)據(jù)分析中本文將重點關(guān)注此種用地類型.

圖2 寧波市季度地價指數(shù)擬合

圖2為浙江全省地價指數(shù)擬合曲線,該曲線各拐點與過往重要政策頒布,市場變化有較好的對應(yīng)關(guān)系,見表2,證明本文方法得到的地價指數(shù)符合過往經(jīng)驗與市場預(yù)期.

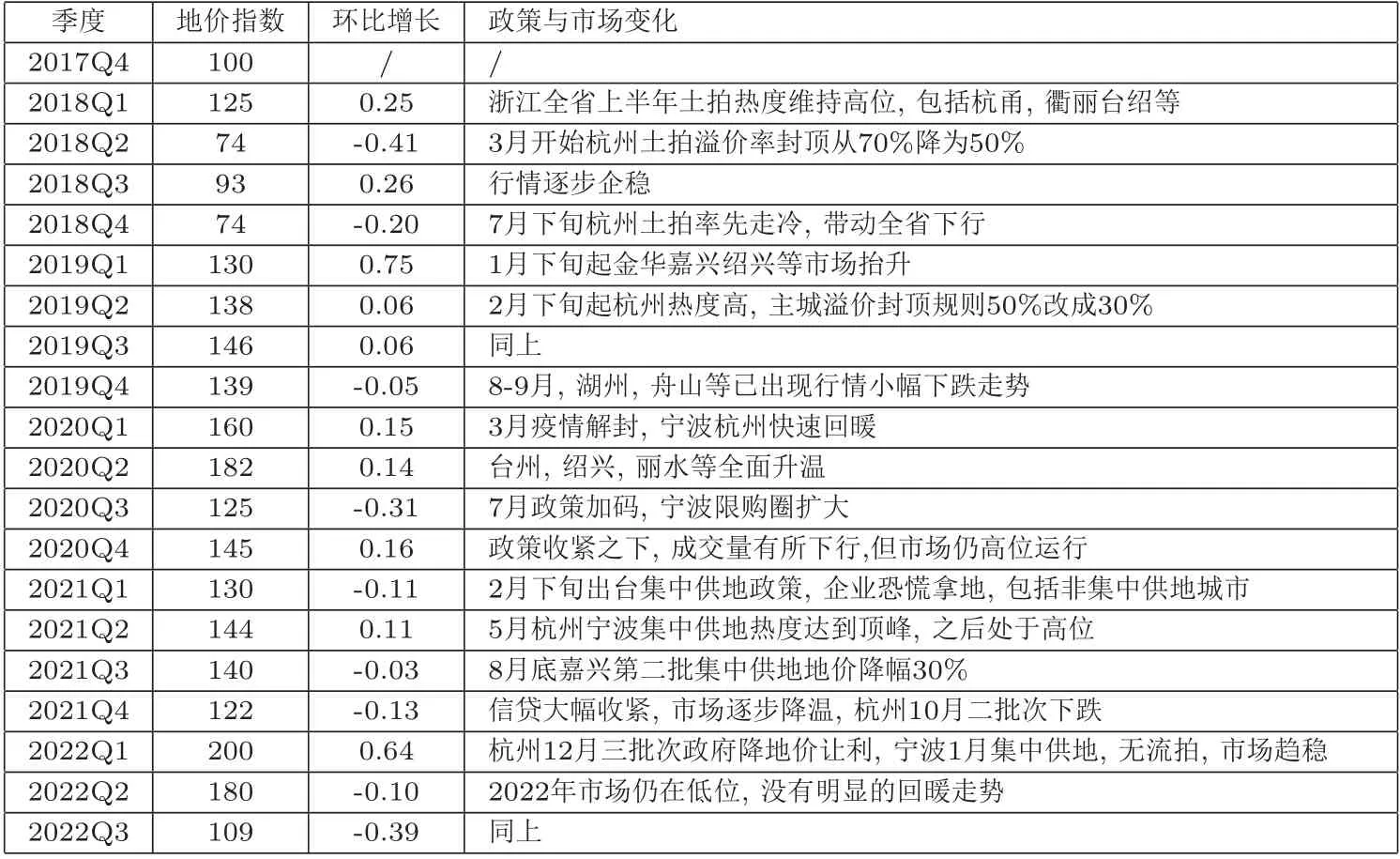
表2 浙江省地價指數(shù)走勢與實際市場情況對比

求得SAR模型的各項參數(shù)后,還可對各季度內(nèi)土地平均價格進行樣本內(nèi)預(yù)測,得到的預(yù)測曲線與真實價格曲線如圖4至圖6所示.圖4至圖6顯示,部分區(qū)域預(yù)測值與實際值高度重合,證明該模型有較好的擬合效果.

由于不同地塊價格的數(shù)量級差距很大,本文使用均方相對誤差作為模型誤差的衡量標準,其定義為

其中yt為地價在第t季度的平均價格.圖4至圖6所述模型均方相對誤差如表3所示.

表3 均方相對誤差

對比地價指數(shù)趨勢圖(圖2與圖3)與平均價格趨勢圖(圖4至圖6),可以看出指數(shù)與地價的變化趨勢并不完全一致,指數(shù)的變動通常比地價滯后一個季度左右,而地價指數(shù)比平均價格更能反應(yīng)一定程度的宏觀經(jīng)濟總體變化.以寧波數(shù)據(jù)為例,2020年第一季度至第二季度,平均價格仍在攀升(見圖6),但地價指數(shù)已經(jīng)下降(見圖2).此時受疫情影響,市場低迷,地價指數(shù)較好捕捉到了這一市場變化.

圖3 浙江省季度地價指數(shù)擬合

圖4 浙江省季度平均地價預(yù)測

圖5 杭州市季度平均地價預(yù)測

圖6 寧波季度平均地價預(yù)測

3.2 指數(shù)動態(tài)預(yù)測

浙江省分用地類型的地價指數(shù)未來四季度預(yù)測如圖7所示,三個類型用地的指數(shù)變化不盡相同,但大體趨勢一致.預(yù)測結(jié)果表明2022年第四季度及2023第一季度地價指數(shù)有上升趨勢,而在2023 年第二季度有下降趨勢.預(yù)測的置信區(qū)間如表4所示.

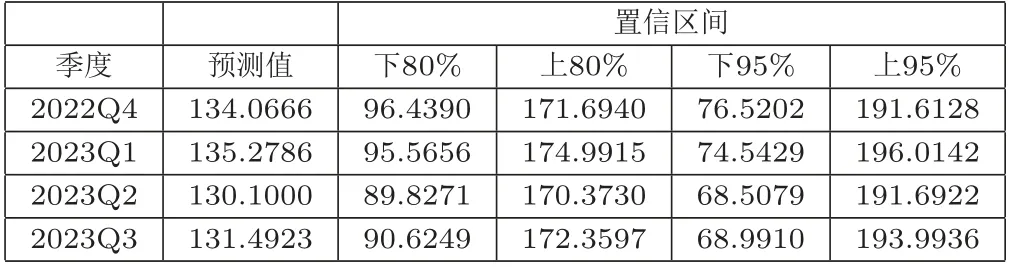
表4 浙江省地價指數(shù)未來四季度區(qū)間估計

圖7 浙江省地價指數(shù)未來四季度點預(yù)測

2.4 地價樣本外預(yù)測

本文提出的空間自回歸模型還可用于地價的樣本外預(yù)測.使用第t期的SAR模型預(yù)測第t+1期的地價,以寧波市t=18(即用2022年第一季度的模型對第二季度地價進行預(yù)測)為例,如圖8所示,平均上看預(yù)測準確度較高,分每個地塊看,預(yù)測值比真實值更加平滑,真實值的波動大,并且有統(tǒng)計意義上的離群點,異常點.圖9為第18期地價預(yù)測值與真實值的箱線圖,可以看出預(yù)測值的中位數(shù)大于真實值,但平均值小于真實值.

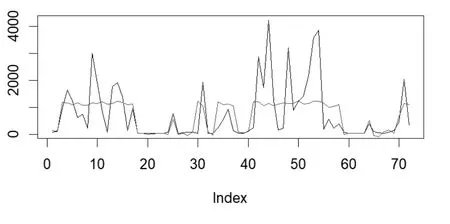
圖8 寧波地價樣本外預(yù)測(橫坐標為第18期各出讓土地地塊,縱坐標為土地價格,紅線為預(yù)測值)

圖9 寧波地價樣本外預(yù)測箱線圖

§3 結(jié)論

本文提出了一個基于空間自回歸的地價指數(shù)擬合預(yù)測模型,能夠較為準確并客觀地刻畫地價指數(shù)在過往的走勢,符合市場經(jīng)驗認知.該模型首先利用空間自回歸模型,刻畫同一時期內(nèi)不同拍賣地塊在地理位置上的相依關(guān)系,再提取出共同趨勢項,利用時間序列模型進行建模.本文所提出的方法均從數(shù)據(jù)本身出發(fā)進行數(shù)學(xué)建模,有別于傳統(tǒng)方法只是對于歷史價格的簡單平均.實證分析結(jié)果表明本文提出的模型對浙江省地價指數(shù)有較好的建模效果.由于缺乏數(shù)據(jù)在時間上的重復(fù)觀測,本文沒有直接通過非平穩(wěn)時空模型(見[11])來進行地價指數(shù)的建模,今后將嘗試這方面的探討.