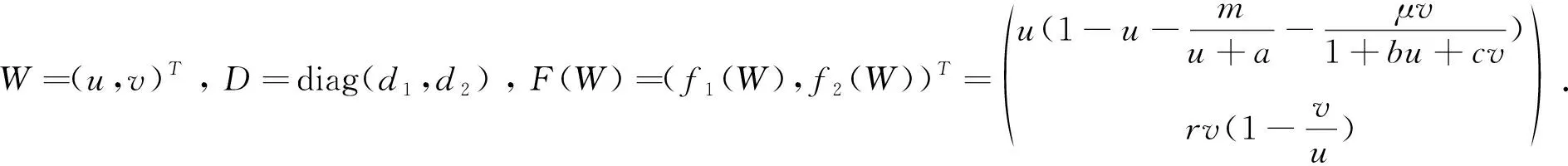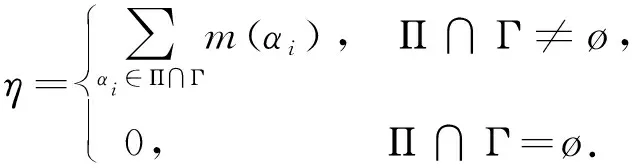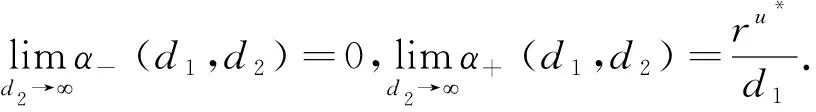一類擴(kuò)散捕食食餌模型的非常數(shù)正穩(wěn)態(tài)解*
高建平,張江洪,練文燕
(贛南師范大學(xué) 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,江西 贛州 341000)
0 引言
種群生態(tài)學(xué)中,兩種群間的相互作用關(guān)系存在多種形式,其中,捕食關(guān)系是一種常見而又基本的種群關(guān)系.繼Lotka和Volterra的兩個(gè)開創(chuàng)性工作[1-2]之后,越來越多的生物數(shù)學(xué)家通過建立微分方程模型來研究捕食關(guān)系[3-5].基于假設(shè)捕食者以logistic形式增長并且其環(huán)境容納量與食餌的種群數(shù)量成正比,給出如下捕食模型的一般形式:

(1)
其中,u和v分別代表食餌,捕食者的種群密度;r表示捕食者的增長率;1/l表示捕食者捕食食餌的轉(zhuǎn)化率;p(u,v)是功能型反應(yīng)函數(shù),它刻畫了捕食者捕食食餌的能力.方程(1)中的捕食者方程是第一次由Leslie和Gower在1960年提出的[6].因此,捕食系統(tǒng)(1)也被稱為Leslie-Gower型捕食食餌模型.針對(duì)不同形式下的功能型反應(yīng)函數(shù)p(u,v),有不少研究者給出了模型(1)的動(dòng)力學(xué)行為研究[7-10].
在模型(1)中考慮捕食者和食餌在空間區(qū)域內(nèi)隨機(jī)游走,便可得到如下反應(yīng)擴(kuò)散的捕食食餌系統(tǒng)
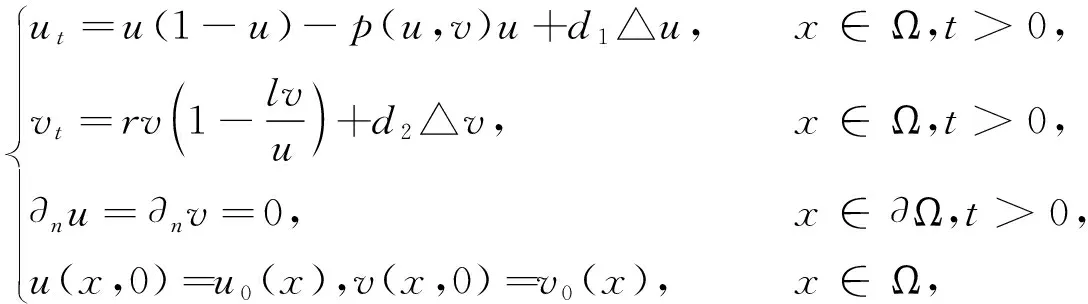
(2)
其中,d1和d2分別代表食餌和捕食者的自擴(kuò)散系數(shù);Ω是有界光滑區(qū)域;n表示邊界?Ω的單位外法向量.在這里,采用了齊次Neumann邊界條件,即在區(qū)域邊界?Ω上沒有種群的進(jìn)出.Shi[11-12]等給出了帶有Ratio-Depenent功能反應(yīng)和Crowley-Martin功能反應(yīng)函數(shù)的擴(kuò)散捕食模型(2)的時(shí)空斑圖動(dòng)力學(xué)研究.Sun[13]等在(2)中考慮Beddington-DeAngelis功能反應(yīng)函數(shù),給出(2)穩(wěn)定性及Turing不穩(wěn)定性研究.對(duì)(2)還存在更多的研究工作[14-16].
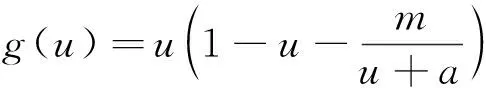
基于此,令l=1,本文在(2)加入組分Allee效應(yīng)并且考慮Beddington-DeAngelis功能反應(yīng)函數(shù),得到

(3)
這里本文假設(shè)0 a0u3+a1u2+a2u+a3=0, (4) 其中,a3=m-a,a2=a+mb+mc+aμ-ab-ac-1,a1=b(a-1)+c(a-1)+μ+1,a0=b+c.注意到a0>0和a3<0,于是,當(dāng)下述條件成立時(shí),方程(4)具有唯一的正根: (5) 因此,當(dāng)條件(5)滿足時(shí),模型(3)具有唯一的內(nèi)部正常數(shù)平衡點(diǎn)E1=(u*,u*). (6) 定理1E0總是不穩(wěn)定的; 證明這里只給出的證明.注意到由條件ru* 與模型(3)對(duì)應(yīng)的穩(wěn)態(tài)解方程為 (7) 要研究模型(3)的非常數(shù)穩(wěn)態(tài)解等價(jià)于研究橢圓系統(tǒng)(7)的非常數(shù)正解. 給出(7)的任意正解的上下界估計(jì).首先,運(yùn)用極值原理[26],得到下面這個(gè)上界估計(jì)結(jié)果. 于是 (8) (9) 下面給出大擴(kuò)散系數(shù)下系統(tǒng)(7)非常數(shù)正解的不存在性結(jié)果. 定理2存在一個(gè)正常數(shù)d*=d*(m,a,b,c,r),使得當(dāng)min{d1,d2}>d*時(shí),(7)不存在非常數(shù)穩(wěn)態(tài)解. (10) (11) 在條件(5)成立的情形下,本小節(jié)將利用Leray-Schauder度理論討論擴(kuò)散系數(shù)變動(dòng)時(shí)模型(3)的非常數(shù)正穩(wěn)態(tài)解的存在性,即研究系統(tǒng)(7)的非常數(shù)正解的存在性.記 將(7)寫成 (12) (d1r-d2ru*)2>-4d1d2r(ru*+σ), (13) 成立時(shí),g(d1,d2;α)=0具有兩個(gè)不同的實(shí)根α-(d1,d2),α+(d1,d2)且滿足α-(d1,d2)<α+(d1,d2),其中 記Π=Π(d1,d2)={α∶α≥0,α∈(α-(d1,d2),α+(d1,d2))},Γ={α0,α1,α2,…}.令m(αi)是特征值αi的重?cái)?shù),根據(jù)文獻(xiàn)[28],可以得到以下引理: α+(d1,d2)∈(αj,αj+1),α- (14) α-(d1,d2)<α+(d1,d2)<α1. (15) (16) 一方面,對(duì)W∈?Λ,有H(W;t)≠0對(duì)所有t∈[0,1]都成立.于是根據(jù)Leray-Schauder度的同倫不變性[28]可知, deg(H(W;0),Λ,0)=deg(H(W;1),Λ,0). (17) 證明這里證明與定理3類似,這里略去.1 常數(shù)平衡點(diǎn)的穩(wěn)定性
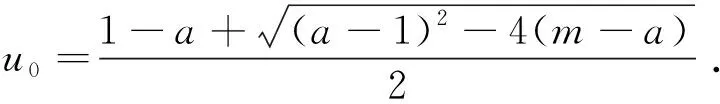
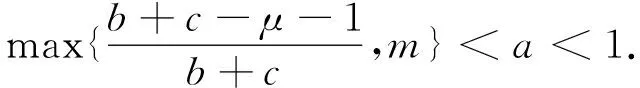




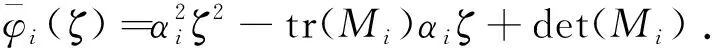
2 非常數(shù)正穩(wěn)態(tài)解的存在性與不存在性
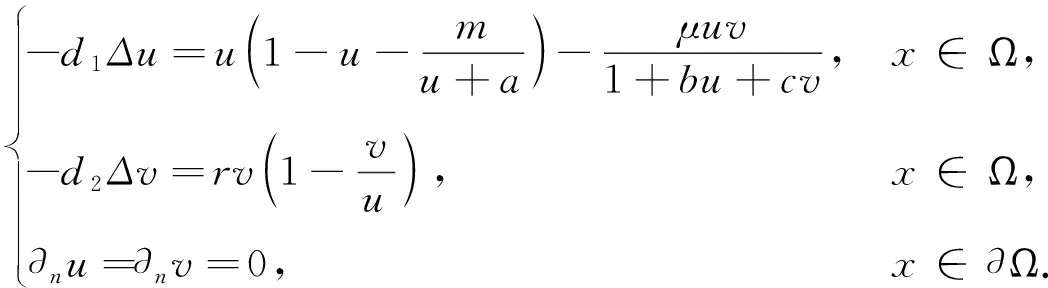
2.1 先驗(yàn)估計(jì)
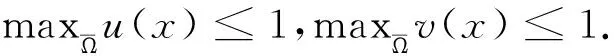


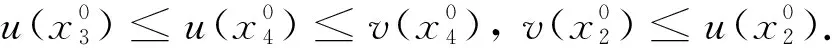

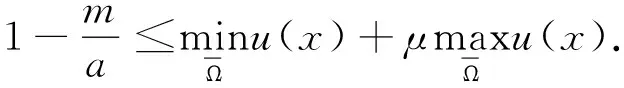
2.2 非常數(shù)穩(wěn)態(tài)解的不存在性

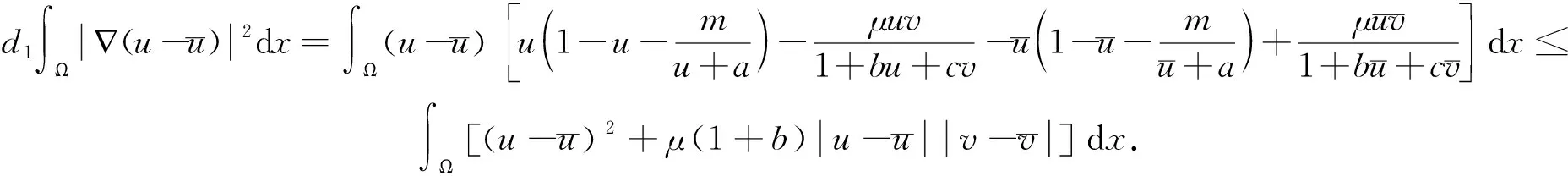



2.3 非常數(shù)穩(wěn)態(tài)解的存在性