江蘇省淮陰中學(xué)教育集團淮安市新淮高級中學(xué)(223001)王恩普

在復(fù)習(xí)基本不等式求最值這類題型時,有部分學(xué)生在解決問題的過程中出現(xiàn)了一些錯誤的解法,但是卻不認為有問題,亦或是感覺有問題又不知錯在哪里,很是困擾,筆者對此進行了深入的探究.

1 錯解呈現(xiàn)

例1已知a>0,b>0,a+b=1,求的最小值.

錯解過程由a> 0,b> 0 知:,當(dāng)且僅當(dāng)時取等號,由可得:此時,則所求最小值為6.

我們知道答案顯然是錯的,那么錯在哪里呢?

2 類比示錯

為了解決這樣的問題,先從一個最基本的求最值問題開始研究:

例2已知x>0,求的最小值.

分析由基本不等式易知: 當(dāng)x>0 時,,當(dāng)且即當(dāng)即x=2 時取等號,即的最小值為4.

但若類比本文開頭的解題邏輯, 也可以這樣處理: 當(dāng)x>0 時,,當(dāng)且僅當(dāng)時即時取等號,此時可得,即的最小值為.

還可以再換一種方案來處理: 當(dāng)x> 0 時,,當(dāng)且僅當(dāng)時即x= 1 時取等號,此時可得,即的最小值為5.

如果繼續(xù)按照類似的方案來處理,將得到更多不同的結(jié)果,此時學(xué)生也意識到根據(jù)基本不等式建立不等關(guān)系,得到取等條件,再根據(jù)取等條件求出的x值回代求最值的思路是存在問題的,文首的雙變量求最值問題亦是如此,但是到底錯在哪里呢?

3 理性釋疑

參考上述錯解過程的做法, 當(dāng)x> 0 時,, 僅僅表示這個不等式是恒成立的, 此時,記,x> 0,則不等式表示的幾何意義是: 在y軸的右側(cè),f(x)的圖象恒在g(x)圖象的上方(可以有交點),如圖1,而取等號的條件對應(yīng)的x則表示f(x)的圖象與g(x)圖象相切時的切點的橫坐標,換言之,若按照這樣的方法求出的最值,其結(jié)果是由左邊配湊后的式子決定的,而將每改變一種配湊形式,將得到不同的函數(shù)g(x),同時切點的位置也隨之變化,而其橫坐標可以取像前文中的1,,亦或是大于0 的每一個數(shù).

結(jié)合開頭展示的正確過程: 由x> 0,根據(jù)基本不等式知:,當(dāng)且僅當(dāng)即x= 2 時取等號,由此可知只有當(dāng)x=2 的時候f(x)取得最小值,那么此時的過程為何正確呢? 繼續(xù)來看圖象,如圖2,此時,g(x) = 4,由于g(x)的圖象是一條與y軸垂直的直線,同時f(x)的圖象恒在g(x)圖象的上方,取等號的條件則對應(yīng)著f(x)的圖象與g(x)圖象的切點處,即x= 2 時f(x)有最小值,此時,也就說明了使用基本不等式求最值時不等號的右側(cè)應(yīng)該是個定值,至此,我們不僅找到了錯誤的根源,也明白了應(yīng)該如何去處理.

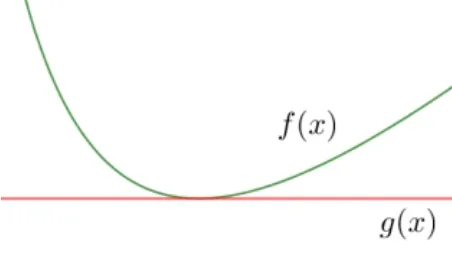
圖2

文章開頭給出借助基本不等式求雙變量類型最值問題,其錯解原因也是一樣的,其實這也是平時提煉出的利用基本不等式求最值時,要注意“一正二定三相等”的原則,“一正”保證了基本不等式可用, 而“二定”則是指使用基本不等式時,不等式的一側(cè)應(yīng)為常數(shù)(不含變量),得到了可能產(chǎn)生的最值,“三相等”則是驗證了最值的存在性,而文首出現(xiàn)的錯誤則是沒有真正理解“二定”的原則.

4 鞏固提升

當(dāng)從根本上理解了錯誤的原因之后,接下來通過一組題來看下此類問題應(yīng)如何處理.

例3已知a>b>0,a+b=1,求的最小值.

解由a>b>0 知a-b>0,且有(a-b)+2b=1,則

評注過程中在上乘以(a-b)+2b,目的是為了配湊出與這兩個積為定值的代數(shù)式,進而求出最值.

例4已知a>b>0,a+b=1,求的最小值.

解由a>0,b>0,a+b=1 知:,當(dāng)且僅當(dāng)時取等號,此時由a+b=1 可得,則的最小值為3.

評注過程中的1 用a+b來代換,其目的也是為了配湊出和這一對積為定值的代數(shù)式,從而使得問題得到解決.

例5已知a>b>0,且,求ab的最小值.

解由a>b> 0 知,當(dāng)且僅當(dāng)時取等號,而,則有,化簡可得ab≥8,由與ab=8 可得a=2,b=4,則ab的最小值為8.

評注本題中雖然開頭運用基本不等式建立的不等關(guān)系的右邊不是定值,但是此時結(jié)合題中的條件可以得到ab≥8,也是符合前文研究的基本不等式求最值的情況,只是稍微間接了一點,此時得到了兩個不等關(guān)系,需要驗證兩個不等式成立的公共條件是否成立.

例6已知a>b>0,求的最小值.

解由題知,當(dāng)且僅當(dāng)a4=1即a=1 時取等號,由a>b>0 知.當(dāng)且僅當(dāng)時取等號, 由a= 1,可得,a=1,,則的最小值為

評注同例5,過程中運用了兩次基本不等式才使得不等式的一側(cè)為常數(shù),則需要去進一步驗證兩次使用基本不等式取等的條件能否同時成立.

5 思想升華

除了利用基本不等式可以直接解決一些最值問題,還可以借助于這種求最值的思想來幫助我們解決一些較為復(fù)雜的問題,而且有著事半功倍的效果.

例7函數(shù)f(x)=xex-ax+b的圖象在x=0 處的切線方程為:y=-x+1.

(1)求a和b的值;

(2)若f(x)滿足: 當(dāng)x> 0 時,f(x) ≥lnx-x+m,求實數(shù)m的取值范圍.

解(1)a=2,b=1.(過程略)

(2)分析 常規(guī)的做法是構(gòu)造函數(shù)直接求最值,但是此時求最值的過程會涉及到隱零點代換等方法, 過程相對復(fù)雜,對學(xué)生的推理能力要求比較高,而下面的解法則較為簡潔.

由f(x) ≥lnx-x+m知,m≤xex-x-lnx+1,由ex≥x+1(當(dāng)且僅當(dāng)x=0 時取等號)知

當(dāng)且僅當(dāng)x+lnx=0 時取等號,令g(x)=x+lnx(x>0),則, 則g(x) =x+ lnx在定義域上單調(diào)遞增, 又,g(e) = e + 1 > 0,則存在x0使得g(x0) = 0, 即x+ lnx= 0 有解, 即有(xex-x-lnx+1)min=2,則m≤2.

評注題中的求最值過程采用了放縮法,正是基本不等式法求最值思想的本質(zhì)體現(xiàn),而放縮法之所以可行,正是因為建構(gòu)的不等式的一側(cè)是定值,而后面的過程則體現(xiàn)了取等這個另一重要的環(huán)節(jié),完美的展現(xiàn)了方法與思想的遷移.

往往一個錯誤的解法都是有其原因的,有時只是根據(jù)提供的解答進行糾正,強行入駐大腦,也許只是過眼云煙,因此,我們有必要去探究這樣的解答錯了沒有,錯在哪里,為什么錯, 對此進行充分研究之后, 才真正的走進深度學(xué)習(xí), 當(dāng)然,在此基礎(chǔ)之上,能將掌握的知識,方法,思想進行發(fā)展,遷移,會將更好的提升自身的創(chuàng)新能力.