Shang Gao(高尚) and Yu-Guang Yang(楊宇光)

Faculty of Information Technology,Beijing University of Technology,Beijing 100124,China

Keywords: quantum algorithm,Toeplitz matrix-vector multiplication,circulant matrix

1.Introduction

Quantum computing has demonstrated its superior performance in solving certain computing problems,such as factoring large numbers[1]and unstructured database searching.[2]In the era of big data,machine learning methods have become increasingly important,but their computational complexity remains high.Due to the high efficiency of quantum computing, increasing numbers of researchers have devoted themselves to the new research field of quantum machine learning(QML)in recent years,hoping to accelerate classical machine learning algorithms with the help of the superposition and entanglement in quantum systems.Representative QML algorithms include positive semidefinite programming,[3]solving linear equations,[4]clustering,[5,6]topology analysis,[7]principal component analysis,[8,9]support vector machines,[10]association rule mining,[11]dimensionality reduction,[12,13]recommendation systems,[14,39]visual tracking,[15,16]the advanced encryption standard,[17]etc.

Toeplitz matrix-vector multiplication is widely used in the fields of optimal control,[18]systolic finite field multipliers,[19]and multidimensional convolution,[20]and thus it has become a hot topic.[18-29]Generally speaking, the Toeplitz matrix is obtained by discretizing a continuous function,and its dimension is connected to the discretization grid parameter.In other words, the Toeplitz matrix can be generated where its diagonal elements are the Fourier transform coefficients of the generating function.Moreover,in practice,the dimensionality of Toeplitz matrices is usually very large; thus,processing them is computationally expensive.Therefore, it is necessary to explore more efficient algorithms to compute matrix-vector products.Wanet al.[30,31]proposed an asymptotic quantum algorithm and a block-encoding-based algorithm,respectively.Although their tasks are to solve the Toeplitz system,they can also be naturally applied to the multiplication of the Toeplitz matrix and vector.However, these algorithms are either inaccurate or depend on theL1-normρof the displacement of the structured matrices(this parameter may be a large value).To solve this problem, in this paper, we will present a nonasymptotic and efficient (independent ofρ) quantum algorithm for Toeplitz matrix-vector multiplication.

The rest of this paper is organized as follows.In Section 2,we review the classical Toeplitz matrix-vector multiplication.Then,we describe the details of the proposed quantum algorithm in Sections 3 and 4.In Section 5,the error and runtime analyses of the proposed quantum algorithm are given.In Section 6,we make a comparison between the proposed quantum algorithm and other existing algorithms.The conclusion is given in Section 7.

2.Classical Toeplitz matrix-vector multiplication

A Toeplitz matrix is ann×nmatrixT= [tk,j;k,j=0,1,...,n-1],wheretk,j=tk-j.

More clearly,a Toeplitz matrix is of the form

namely, all elements along each diagonal direction in a Toeplitz matrix are constants.In practice, the Toeplitz matrices are usually obtained by discretizing continuous functions;[32]namely, the diagonal elementsofTare the Fourier transform coefficients of a functioni.e.,

wheredenotes the set of all 2π-periodic strictly positive continuous real-valued functions defined on [0,2π].[33]The functionfis called the generating function of the sequence of the Toeplitz matrixT.[34]The Toeplitz matrixTwill be Hermitian iffis a real-valued function.And whenTis Hermitian,its eigenvalues are represented asσk,satisfying

wherefminandfmaxrepresent the minimum and maximum values off, respectively.Note that the generating functionfis strictly positive and thus the Toeplitz matrixTis nonsingular.[35]For a further description of Toeplitz matrices,see Ref.[36].

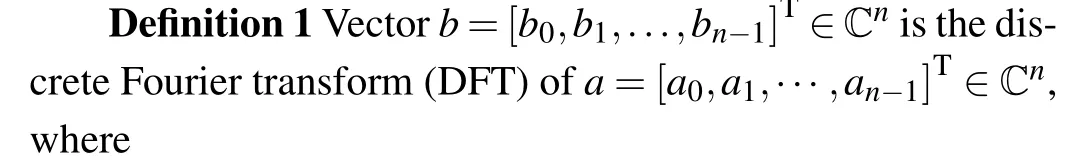
andω=.

To be specific,

The circulant matrix is a special kind of Toeplitz matrix with the form

wherec=[c0,c1,...,cn-1]T.Specifically,each column of the circulant matrix is a downward circular shift of the column preceding it, which means that the circulant matrixC(c) can be determined by its first columnc.

Obviously,any circulant is a matrix polynomial(namely,the associated polynomial)in the cyclic permutation matrixL,i.e.,

whereLis given by

From this we can get

where

So,

where

Obviously,Eq.(12)is an eigen-decomposition of the circulant matrix, and it is also a unitary decomposition.Here,λjare the eigenvalues of the matrixC(c), and can be calculated by Eq.(14),i.e.,by performing a fast Fourier transform(FFT)on the vectorc.

Therefore, for any vectorx, the product of the circulant matrixC(c)andxcan be calculated as follows:

where⊙denotes element-wise multiplication.

To compute the Toeplitz matrix-vector productTx=y,Tis first embedded into a large circulant matrix of size 2n:

where

In fact,we have exactly[36]

Specifically, the eigenvalues ofC(c) are simply the values off(ι) withιuniformly spaced between 0 and 2π.Defining 2πk/n=ιk,for any powers,we have[36]

where the continuity off(ι) guarantees the existence of the limit of Eq.(20)as a Riemann integral.

Finally, the product ofTand any vectorxcan be calculated by multiplying the circulant matrixC(c) with the extended vector

3.Quantum Toeplitz matrix-vector multiplication

In this section, we design a quantum algorithm for Toeplitz matrix-vector multiplication.Specifically,we bypass the phase estimation operation commonly used in other quantum algorithms by taking full advantage of the special properties of Toeplitz matrices.

The proposed quantum algorithm is formally introduced below.

(1)Generate the initial quantum state

(2) Apply an inverse quantum Fourier transform(QFT)[37]on|χ〉,and yield

(3) Similar to Ref.[30], suppose there is an Oracle that accesses the values (eigenvalues ofC(c)) of the generating functionf:

The cost of invoking the Oracle isO(1).It can be known from Eq.(19)that the eigenvalues of the circulant matrixC(c)can be directly calculated by the generating function.From Eqs.(14)and(15),it can be seen that the element-by-element multiplication of the eigenvalues with the vector after the discrete Fourier transform will be used in the calculation of the product of the circulant matrix and the vectorx0.In this quantum version of the operation, the implementation steps are as follows.

(4)Add an ancillary qubit and perform a controlled rotation on it to get the state

(7)Discard the last qubit in the quantum register and yield|y〉after performing the“incomplete”QFT.

4.Special case

In the previous section we gave a quantum algorithm for Toeplitz matrix-vector multiplication with a known generating functionf.However,in some special cases only the Toeplitz matrices are given while the generating function is unknown.In view of these situations, in this section we will design another quantum algorithm.

Similarly, in the quantum random access memory(QRAM)[38,39]data structured model,one can also prepare the quantum stateOc|0〉→|c〉=∑i ci|i〉/‖c‖with time complexityO(polylogn).

A formal description of the quantum algorithm is given below.

(1)Prepare the initial quantum state

(2)Apply an inverse QFT on|χ〉and perform a Hadamard gate on the qubit|0〉in the second register,resulting in

(3)Perform a controlled quantum gate to the third register of log2nqubits,and obtain

(4) Perform a controlled QFT operation on the qubits in the third register,and the quantum state becomes

(5) Repeat a Hadamard gate operation on the auxiliary qubit in the second register,get

where

And

(6) According to the quantum amplitude estimation(QAE)[37,40]algorithm,get

(7)Append an extra register and perform a quantum arithmetic operation on it to obtain

(8)Add an ancillary qubit and perform a controlled rotation on it,and obtain

(9)Uncompute quantum registers,except for the first and last registers, and then measure the last ancillary qubit to see|0〉,and transform the system to

In this special case, when the generating function is unknown, to calculate the eigenvalues of the circulant matrix,it is necessary to calculate the discrete Fourier transform of a specific vectorc.And this is exactly what the previous series of steps have done.

(10)Discard the last qubit in the quantum register and obtain|y〉 after performing the “incomplete” QFT on the quantum state in Eq.(37).

5.Complexity analysis

In this section,we will give the complexity analysis of the proposed quantum algorithms for Toeplitz matrix-vector multiplication.We first analyze the complexity of the first quantum algorithm with the generating function.The complexity of preparing the initial quantum state and that of performing the(inverse)QFT are bothO(polylogn).In the measurement operation, the success probability of obtaining the measurement|0〉is

In step (9), the probability of getting the measurement outcome|0〉is

Similarly,according to the error analysis in Ref.[4],introducing an error ofO() when calculatingλjwill result in an error of ?0in the final resulty.In conclusion, the time complexity of the second quantum algorithm with the unknown generating functionfis

6.Discussion

In this paper,we have proposed a quantum algorithm for Toeplitz matrix-vector multiplication by taking full advantage of the properties of Toeplitz matrices.The table below shows a comparison between our proposed quantum algorithms and other quantum algorithms.

Table 1.A comparison of existing quantum algorithms. κ＇ is the condition number of the Toeplitz matrix.

In Ref.[41], Zhouet al.also presented a quantum algorithm for Toeplitz matrix-vector multiplication,for the case where the generating function is not known,and its time complexity is,which greatly depends on||C|x〉||and||T|x〉||.In addition, in Ref.[30], Wanet al.gave two asymptotic quantum algorithm frameworks works that focused on resolving the Toeplitz system, corresponding to the cases with and without the generating function, respectively.But it can also be used to calculate the multiplication of the Toeplitz matrix and vector.Later, they proposed a blockencoding-based quantum algorithm,[31]whose time complexity has a linear dependence onρ.As a conclusion, for the well-conditioned matrices, i.e.,κ=κ＇=O(polylogn), the proposed quantum algorithms are two exact algorithms with the time complexity independent ofρ(this number may be very large).

In addition,it is worth mentioning that the proposed quantum algorithms can be extended to the case with Hankel matrices.To be more specific, ann×nHankel matrix is of the form

It can be observed that if the columns are permuted left-toright,thenHwill become a Toeplitz matrixT.Therefore,the following relation holds:

Thus,it becomes a Toeplitz matrix-vector multiplication.

7.Conclusion

In this article, we present two accurate and efficient quantum algorithms for Toeplitz matrix-vector multiplication.Specifically,we first present a non-asymptotic quantum algorithm for Toeplitz matrix-vector multiplication with time complexityO(κpolylogn).For the case with an unknown generating function, we also give a corresponding non-asymptotic quantum version that eliminates the dependency on theL1-normρof the displacement of the structured matrices.Actually, the proposed quantum algorithms benefit from taking full advantage of the special properties of Toeplitz matrices.Here,we hope that the proposed quantum algorithms can provide some inspiration to researchers in related fields.

Acknowledgements

We thank S.-J.Pan and L.-C.Wan for fruitful discussions.This work was supported by the National Natural Science Foundation of China(Grant Nos.62071015 and 62171264).