宋 偉, 韓佳虎, 李 峰*, 曹晴峰

(1.江蘇理工學(xué)院 電氣信息工程學(xué)院, 江蘇 常州 213001; 2.揚(yáng)州大學(xué) 電氣與能源動(dòng)力工程學(xué)院, 江蘇 揚(yáng)州 225127)

0 引言

Hammerstein非線性模型同時(shí)結(jié)合了動(dòng)態(tài)線性特征和無(wú)記憶非線性特征,可以描述一大類實(shí)際非線性過程,被廣泛應(yīng)用于實(shí)際工業(yè)過程的辨識(shí)建模與控制.圍繞Hammerstein模型的參數(shù)辨識(shí)問題,領(lǐng)域內(nèi)的專家研究出了一些重要的方法,主要分為同步辨識(shí)和分步辨識(shí)兩大類.同步辨識(shí)包括過參數(shù)化法[1,2],子空間法[3,4],直接辨識(shí)法[5,6]等,這類辨識(shí)方法通過構(gòu)造系統(tǒng)的混合參數(shù)模型,直接辨識(shí)原模型混合參數(shù),然后進(jìn)行各子系統(tǒng)參數(shù)分離.分步辨識(shí)包括迭代法[7,8],頻域法[9],多信號(hào)源法[10-13]等,這類辨識(shí)方法通過重構(gòu)中間變量,實(shí)現(xiàn)模型子系統(tǒng)之間的參數(shù)分離辨識(shí).

在Hammerstein非線性模型的參數(shù)辨識(shí)中,最小二乘方法因其概念簡(jiǎn)單、易于實(shí)現(xiàn)而成為非線性模型辨識(shí)的主流算法[14].考慮SISO(Single Input Single Output)Hammerstein模型的辨識(shí)問題,文獻(xiàn)[15]在遞推最小二乘算法中引入變遺忘因子,解決了由于參數(shù)映射帶來(lái)的收斂速度下降問題.基于關(guān)鍵項(xiàng)分離技術(shù),Ding等[16]將Hammerstein受控自回歸系統(tǒng)分解為若干個(gè)變量較少的子系統(tǒng),利用遞階最小二乘算法辨識(shí)子系統(tǒng)參數(shù).文獻(xiàn)[17]針對(duì)Hammerstein非線性輸出誤差系統(tǒng),利用輔助模型的輸出代替未知變量,提出了一種基于輔助模型的最小二乘辨識(shí)算法.考慮一類輸入非線性誤差系統(tǒng),文獻(xiàn)[18]將關(guān)鍵項(xiàng)分離技術(shù)結(jié)合輔助模型方法,研究了基于關(guān)鍵項(xiàng)分離的輔助模型最小二乘辨識(shí)方法.上述方法中研究了Hammerstein模型的外部噪聲為白噪聲的參數(shù)辨識(shí)問題,得到一致的參數(shù)估計(jì).

系統(tǒng)的外部噪聲有兩種形式,即白噪聲和有色噪聲.與白噪聲相比,有色噪聲具有一般性和代表性[19].當(dāng)外部噪聲為有色噪聲時(shí),上述各類最小二乘辨識(shí)方法無(wú)法得到系統(tǒng)參數(shù)的一致估計(jì)[14],其原因是遞推辨識(shí)算法沒有對(duì)噪聲模型的參數(shù)進(jìn)行估計(jì),因此對(duì)有色噪聲干擾下Hammerstein模型辨識(shí)的關(guān)鍵在于能夠有效估計(jì)有色噪聲模型.根據(jù)有色噪聲的產(chǎn)生機(jī)理,有色噪聲可由白噪聲生成[20],可以利用自回歸模型[21],滑動(dòng)平均模型[22,23],或者自回歸滑動(dòng)平均模型[24]進(jìn)行擬合.針對(duì)帶有色噪聲的狀態(tài)空間模型的辨識(shí)問題,文獻(xiàn)[25]基于遞階辨識(shí)原理,推導(dǎo)了狀態(tài)觀測(cè)器的遞階隨機(jī)梯度算法,對(duì)參數(shù)向量和狀態(tài)進(jìn)行聯(lián)合估計(jì).考慮一類Hammerstein FIR-MA-like系統(tǒng),文獻(xiàn)[26]基于數(shù)據(jù)濾波技術(shù),探究了一種基于數(shù)據(jù)濾波隨機(jī)梯度辨識(shí)方法.針對(duì)Hammerstein非線性受控自回歸滑動(dòng)平均系統(tǒng),文獻(xiàn)[24]研究了一種基于牛頓迭代的最大似然估計(jì)方法.上述文獻(xiàn)研究了不同類型有色噪聲干擾的Hammerstein模型辨識(shí)方法,并取得相應(yīng)的辨識(shí)結(jié)果.值得強(qiáng)調(diào)的是上述辨識(shí)方法在辨識(shí)過程中出現(xiàn)Hammerstein模型參數(shù)乘積項(xiàng),在設(shè)置非線性子系統(tǒng)或者線性子系統(tǒng)的首項(xiàng)參數(shù)為1的條件下分離出線性和非線性子系統(tǒng)的參數(shù)值.因此這類方法降低了模型辨識(shí)精度,且具有一定的局限性.

針對(duì)上述問題,本文考慮一類滑動(dòng)平均噪聲的干擾,研究了有色噪聲干擾下Hammerstein模型參數(shù)分離辨識(shí).研究中設(shè)計(jì)了由二進(jìn)制信號(hào)和隨機(jī)信號(hào)構(gòu)成的組合信號(hào),并利用二進(jìn)制信號(hào)不激發(fā)靜態(tài)非線性子系統(tǒng)的特性實(shí)現(xiàn)Hammerstein模型各串聯(lián)子系統(tǒng)分離辨識(shí),解決了Hammerstein模型中間變量信息不可測(cè)量問題.首先,基于二進(jìn)制信號(hào)的輸入/輸出數(shù)據(jù),采用AV-RELS(Auxiliary Variables Recursive Extended Least Squares)方法辨識(shí)線性子系統(tǒng)和滑動(dòng)平均噪聲模型的參數(shù),實(shí)現(xiàn)參數(shù)一致估計(jì).其次,基于隨機(jī)輸入信號(hào)及其輸出,通過本文提出的FF-ESG(Forgetting Factor based Extended Stochastic Gradient)方法,可以有效的改善非線性子系統(tǒng)的辨識(shí)效果.

1 滑動(dòng)平均噪聲干擾下Hammerstein非線性模型

考慮如圖1所示的一類滑動(dòng)平均噪聲干擾下Hammerstein非線性模型.

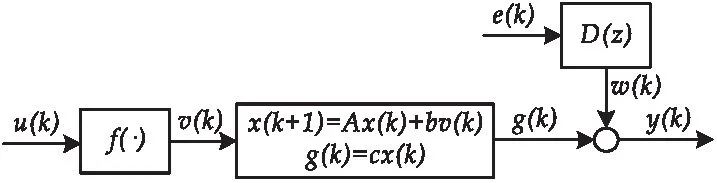
圖1 滑動(dòng)平均噪聲干擾下Hammerstein非線性模型結(jié)構(gòu)圖

根據(jù)圖1所示,滑動(dòng)平均噪聲干擾下Hammerstein模型的數(shù)學(xué)描述如下所示:

v(k)=f(u(k))

(1)

x(k+1)=Ax(k)+bv(k)

(2)

g(k)=cx(k)

(3)

w(k)=D(z)e(k)

(4)

y(k)=g(k)+w(k)

(5)

式(1)～(5)中:f(·)表示靜態(tài)非線性子系統(tǒng),u(k)和v(k)分別是非線性子系統(tǒng)的輸入和輸出,g(k)是線性子系統(tǒng)的輸出,y(k)是Hammerstein模型的輸出.e(k)和w(k)分別是有色噪聲模型的輸入和輸出,D(z)=1+d1z-1+…+dndz-nd是單位后移算子的多項(xiàng)式,dj是噪聲參數(shù),nd是噪聲模型的階次.x(k)是狀態(tài)空間變量的矩陣x(k)=[x1(k),x2(k),…,xn(k)]T,A是狀態(tài)空間的參數(shù)矩陣,b和c是狀態(tài)空間的參數(shù)向量,b=[b1,b2,…,bn]T,c=[1,0,…,0],

采用多項(xiàng)式模型擬合Hammerstein模型的非線性子系統(tǒng),非線性子系統(tǒng)的表達(dá)式如下:

v(k)=f(u(k))=
p1h1(u(k))+p2h2(u(k))+…+
prhr(u(k))=hT(u(k))P

(6)

式(6)中:P=[p1,p2,…,pr]T∈Rr×1是多項(xiàng)式模型的參數(shù)向量,hT(u(k))是關(guān)于輸入u(k)的基函數(shù)向量,h(u(k))=[h1(u(k)),h2(u(k)),…,hr(u(k))]T.

對(duì)于滑動(dòng)平均噪聲干擾下的Hammerstein非線性模型辨識(shí)問題,我們的目標(biāo)是對(duì)于任意給定的閾值ε,求解滿足下列約束條件的參數(shù):

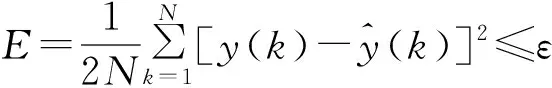
(7)

式(7)中:“∧”表示估計(jì),N表示模型的數(shù)據(jù)長(zhǎng)度.

2 滑動(dòng)平均噪聲干擾下的Hammerstein模型參數(shù)辨識(shí)

為了解決中間變量v(k)不可測(cè)的問題,設(shè)計(jì)特殊的組合式信號(hào)實(shí)現(xiàn)Hammerstein模型參數(shù)的分離辨識(shí).所設(shè)計(jì)的組合式信號(hào)包括幅值為0或λ的二進(jìn)制信號(hào)和隨機(jī)信號(hào).前期的研究結(jié)果表明[27,28]:當(dāng)二進(jìn)制信號(hào)作為輸入信號(hào)u(k)時(shí),非線性子系統(tǒng)的輸出信號(hào)v(k)也是二進(jìn)制信號(hào),即v(k)與u(k)是同頻率不同幅值的二進(jìn)制信號(hào),如圖2(a)所示.使用常數(shù)增益β對(duì)u(k)的幅值進(jìn)行補(bǔ)償,中間變量v(k)就可以用輸入信號(hào)u(k)代替,如圖2(b)所示.因此,可以實(shí)現(xiàn)靜態(tài)非線性子系統(tǒng)和動(dòng)態(tài)線性子系統(tǒng)的參數(shù)分離辨識(shí).

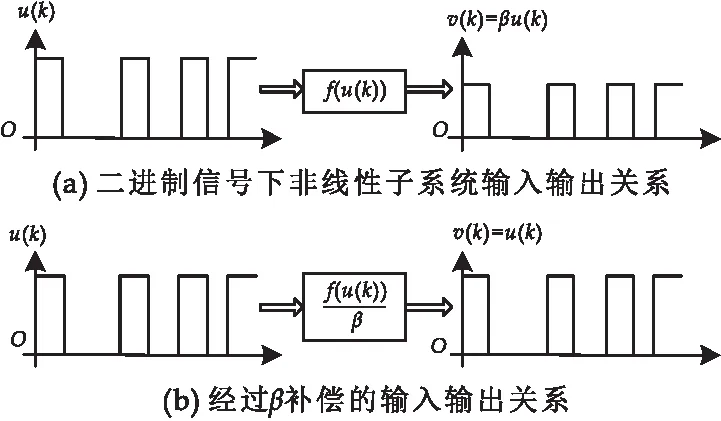
圖2 二進(jìn)制信號(hào)在非線性系統(tǒng)下的特性

2.1 動(dòng)態(tài)線性子系統(tǒng)和滑動(dòng)平均噪聲模型的參數(shù)辨識(shí)

當(dāng)Hammerstein模型的輸入為二進(jìn)制信號(hào)u1(k)時(shí),根據(jù)公式(2)可以得到:

xi(k+1)=xi+1(k)+biv(k)(i=1,2,…,n-1)

(8)

xn(k+1)=-anx(k)-an-1x(k)-…-
a1x(k)+bnv(k)

(9)

利用單位后移算子z-1的性質(zhì),分別在公式(8)的兩邊同時(shí)乘以z-1,公式(9)的兩邊同時(shí)乘以z-n,然后可以得到:

(10)

公式(10)可以簡(jiǎn)化為:

(11)

根據(jù)公式(3)～(5)和公式(11),Hammerstein系統(tǒng)的輸出表達(dá)式為:

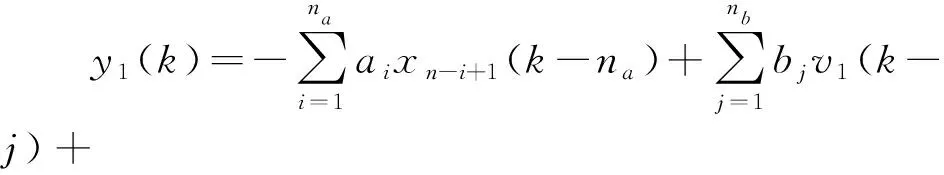
(12)

利用二進(jìn)制信號(hào)的特殊性質(zhì),公式(12)中的v1(k)可以用b0u1(k)代替:

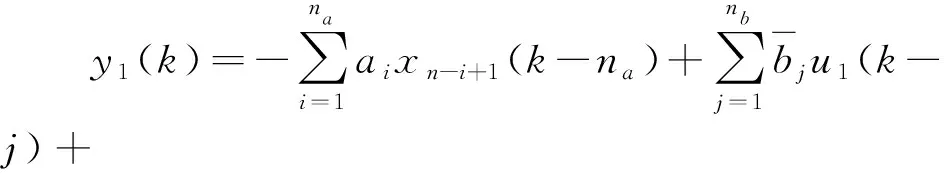
(13)

將公式(13)寫成線性回歸形式:

(14)

式(14)中:θ1=[a1,…,ana,b1,…,bnb,d1,…,dnd]T,φ1(k)=[-xna(k-na),…,-x1(k-na),u1(k-1),…,u1(k-nb),e(k-1),…,e(k-nd)]T.

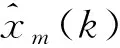
定義準(zhǔn)則函數(shù)如下:

(15)

可以推導(dǎo)基于輔助變量的遞推增廣最小二乘算法,辨識(shí)出線性子系統(tǒng)和滑動(dòng)平均噪聲模型的參數(shù).

(16)

(17)

(18)

(19)

(20)

2.2 靜態(tài)非線性子系統(tǒng)的參數(shù)辨識(shí)

為了辨識(shí)靜態(tài)非線性子系統(tǒng)的參數(shù),采用隨機(jī)信號(hào)u2(k)作為Hammerstein模型的輸入,根據(jù)公式(6)和公式(12),可以得到輸入輸出表達(dá)式:

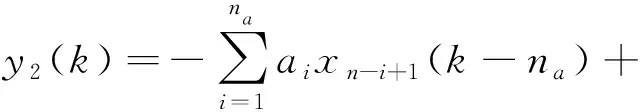
(21)

轉(zhuǎn)化為線性回歸形式:

(22)

定義準(zhǔn)則函數(shù)如下:

(23)

針對(duì)定義的準(zhǔn)則函數(shù),將增廣隨機(jī)梯度算法用于參數(shù)辨識(shí).為了提高辨識(shí)精度,在增廣隨機(jī)梯度算法的基礎(chǔ)上引入遺忘因子[15,29],推導(dǎo)了如下遺忘因子增廣隨機(jī)梯度算法:

(24)

(25)

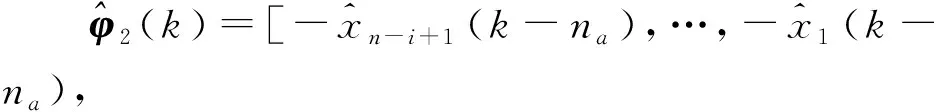
(26)

(27)

(28)

3 仿真研究

為了證明提出的算法的有效性,采用本文提出的算法對(duì)滑動(dòng)平均噪聲干擾下的Hammerstein非線性模型進(jìn)行參數(shù)辨識(shí).考慮如下Hammerstein非線性模型

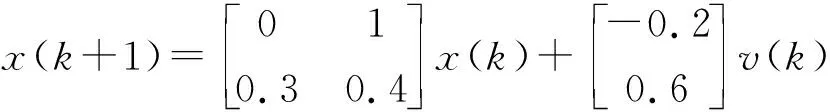
(29)

定義噪信比為

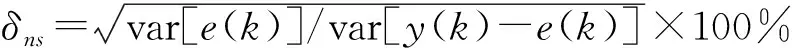
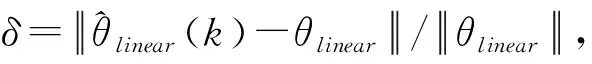
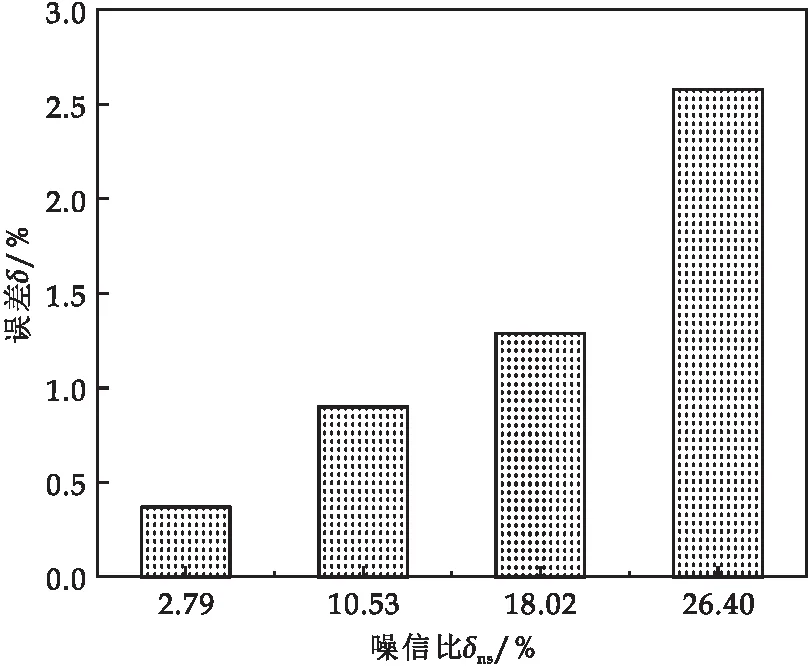
圖3 不同噪信比下的參數(shù)辨識(shí)誤差

噪信比是指模型中噪聲與信號(hào)的比例,噪信比δns越大,表示噪聲對(duì)模型的影響越大,反之則越小.為了說(shuō)明提出的方法能夠有效處理有色噪聲的干擾,圖3選取了四類不同噪信比,且逐漸增加.從圖3中容易看出,隨著噪信比δns的增加,線性子系統(tǒng)參數(shù)辨識(shí)的誤差百分比雖然有所增加,但總體相對(duì)穩(wěn)定,且不超過30%.因此,本文提出的方法能夠有效辨識(shí)有色噪聲干擾下的Hammerstein模型.

為了說(shuō)明提出的方法和加權(quán)增廣隨機(jī)梯度方法[30]對(duì)有色噪聲模型參數(shù)的辨識(shí)效果,圖4和圖5選取了兩類不同噪信比,且逐漸增加.

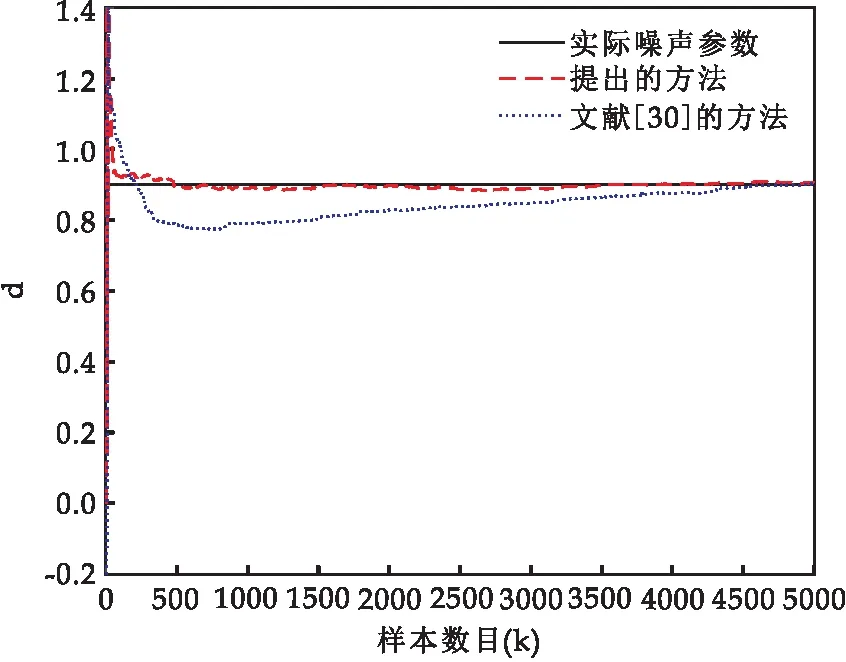
圖4 δns=6.61%時(shí)噪聲參數(shù)辨識(shí)結(jié)果

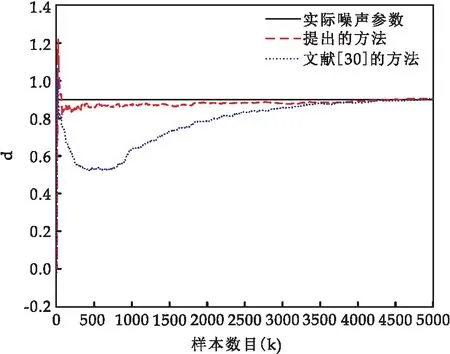
圖5 δns=15.67%時(shí)噪聲模型參數(shù)辨識(shí)結(jié)果

從圖4和圖5中可看出,與加權(quán)增廣隨機(jī)梯度方法相比,本文提出方法的噪聲模型參數(shù)的估計(jì)值更接近真實(shí)值.隨著噪信比δns的增加,本文提出方法的效果更加明顯.

第二階段：根據(jù)隨機(jī)信號(hào)及其對(duì)應(yīng)的輸出信號(hào),采用2.2節(jié)推導(dǎo)的遺忘因子增廣隨機(jī)梯度算法對(duì)非線性子系統(tǒng)進(jìn)行辨識(shí).仿真中,遺忘因子λ=0.877.為了更好的證明所提出算法的優(yōu)越性,將推導(dǎo)的算法與RELS算法[31],GI算法(Gradient-based Iterative)[32]和AM-RELS算法(Auxiliary model based Recursive Extended Least Squares algorithm)[33]進(jìn)行對(duì)比,四種算法對(duì)非線性子系統(tǒng)的擬合結(jié)果如圖6和表1所示.

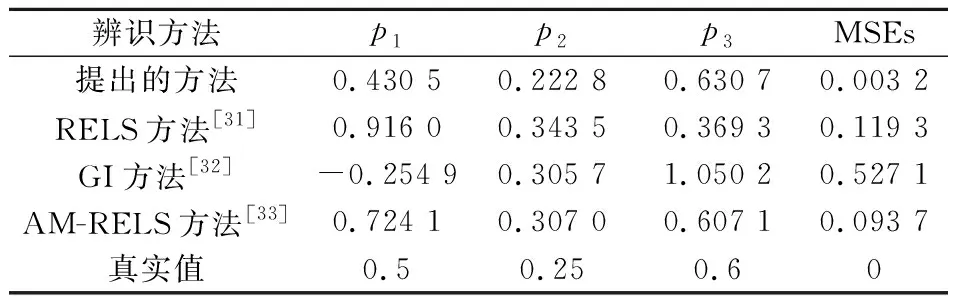
表1 非線性子系統(tǒng)的辨識(shí)誤差

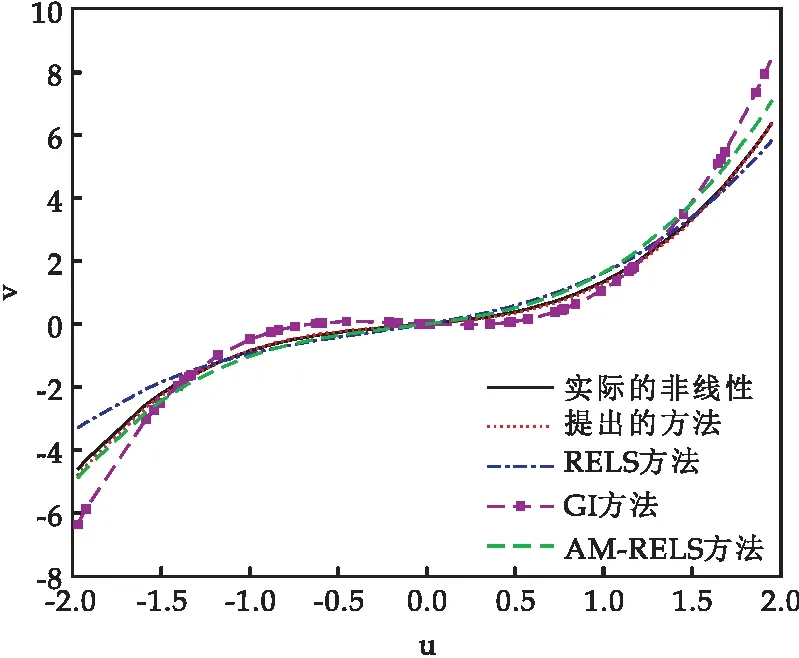
圖6 四種辨識(shí)算法對(duì)非線性擬合結(jié)果比較

從圖6和表1可看出,相較于RELS方法,GI方法以及AM-RELS方法,本文推導(dǎo)的方法在對(duì)Hammerstein模型的非線性子系統(tǒng)辨識(shí)時(shí),具有更高的辨識(shí)精度.本文提出的遺忘因子增廣隨機(jī)梯度方法,由于在算法中引入遺忘因子,增加記憶長(zhǎng)度,使辨識(shí)精度提高.迭代梯度方法遍歷整個(gè)數(shù)據(jù)集時(shí),每次更新并不是向著最優(yōu)的方向進(jìn)行,往往出現(xiàn)局部最優(yōu),導(dǎo)致無(wú)法得到整體最優(yōu)解.遞推增廣最小二乘非線性辨識(shí)方法雖然收斂速度較快,但在有色噪聲干擾下效果不理想.輔助模型遞推增廣最小二乘方法在辨識(shí)過程中因輔助模型階次的選擇不同,導(dǎo)致辨識(shí)結(jié)果存在一定的偏差.

增廣隨機(jī)梯度(ESG)方法計(jì)算量小,但收斂速度慢.為了提高增廣隨機(jī)梯度方法的收斂速度和辨識(shí)精度,在增廣隨機(jī)梯度方法中引入遺忘因子.遺忘因子是誤差準(zhǔn)則函數(shù)中的加權(quán)因子,不同的遺忘因子代表對(duì)舊數(shù)據(jù)不同的遺忘速度.隨著遺忘因子增大,模型的收斂速度加快,但誤差變大;隨著遺忘因子減小,模型的誤差變小,但收斂速度變慢.因此,選擇合適的遺忘因子可以平衡收斂速度和誤差.從圖7可以看出,當(dāng)遺忘因子λ=0.877時(shí),非線性子系統(tǒng)擬合效果最好.

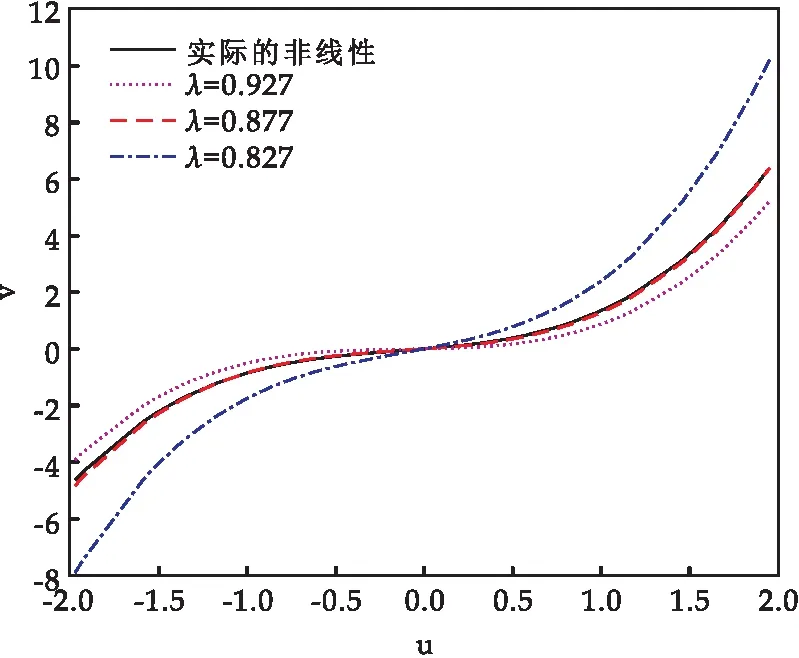
圖7 不同遺忘因子的非線性擬合結(jié)果比較

4 結(jié)論

本文針對(duì)有色噪聲干擾的Hammerstein模型的參數(shù)辨識(shí)問題,提出了一種智能分離辨識(shí)方法.通過設(shè)計(jì)特殊的組合式信號(hào),分別對(duì)靜態(tài)非線性子系統(tǒng)和動(dòng)態(tài)線性子系統(tǒng)進(jìn)行參數(shù)辨識(shí).首先,采用二進(jìn)制信號(hào)作為Hammerstein模型的輸入,分析其不激發(fā)非線性子系統(tǒng)的性質(zhì),通過AV-RELS方法辨識(shí)出線性子系統(tǒng)和有色噪聲模型的參數(shù).其次,將系統(tǒng)的不可測(cè)狀態(tài)變量用估計(jì)值代替,利用隨機(jī)信號(hào)的輸入輸出數(shù)據(jù),采用FF-ESG方法得到非線性子系統(tǒng)的參數(shù).仿真結(jié)果驗(yàn)證了所推導(dǎo)的智能分離算法Hammerstein模型的參數(shù)具有較高的辨識(shí)精度.