Jian-Zheng Li(李建政), Guan-Ling Li(李觀玲), and Wen-Lei Zhao(趙文壘)

School of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China

Keywords: super-ballistic diffusion,Bose–Einstein condensate,nonlinear interaction,non-Hermiticity

1.Introduction

Quantum diffusion of Floquet-driven systems[1–6]has garnered significant attention across various fields of physics,including quantum chaos and condensed matter physics.[7–15]The quantum kicked rotor (QKR), a paradigmatic model of quantum chaos, exhibits a well-known phenomenon of dynamical localization (DL),[16,17]which is analogous to Anderson localization of electrons in disordered lattices.[18,19]The quasi-periodic quantum kicked rotor (QPQKR) withNincommensurable frequencies, a variant of the QKR model induced by modulating the kicking potential, can emulate theN-dimensional Anderson model in coordinate representation,[16,20,21]offering an ideal platform for verifying the scaling law of Anderson transitions.Theoretical investigations on quantum diffusion of the QPQKR have been observed in state-of-the-art experiments involving Bose–Einstein condensates(BEC)of ultra-cold atoms.[22–28]Previous investigations have shown that the nonlinear interaction of BEC atoms,a mean-field approximation of many-body interaction,induces sub-diffusion in the QPQKR model governed by the Gross–Pitaevskii(GP)equation.[29–35]

It is widely recognized that an open system interacting with its environment can be described by a non-Hermitian Hamiltonian.[36–40]The non-Hermitian extension to Floquetdriven systems has stimulated numerous studies on quantum diffusion behaviors.[41–44]For instance, when a general non-Hermitian driving potential is introduced to coupled QKRs,the phenomenon of DL is effectively protected due to novel quantum coherence.[45]Interestingly, when aPT-symmetric non-Hermitian driving potential is applied to a QKR system with nonlinear interaction, super-exponential diffusion emerges as a result of the non-Hermitian modulation of the nonlinear interaction.[46]In this context, the diffusion behaviors arising from the interplay between nonlinearity and non-Hermiticity in the QPQKR model deserve urgent investigation.

In this work,we investigate the quantum diffusion of BEC by utilizing a nonlinear and non-Hermitian extension of the QPQKR model.When the strength of the non-Hermitian driving potential is weak, the system displays two classes of energy diffusion, namely the DL and subdiffusion (SD) corresponding to weak and strong nonlinear interactions, respectively.As the non-Hermitian parameter is sufficiently large,we can find a transition from SBD to AD and then to CD with the increase of nonlinearity.We numerically ascertain the diffusion exponent and the diffusion coefficient of mean energy across a broad range of system parameters,which can is useful for the Floquet engineering of energy diffusion.Notably, we identify a prethermalization stage preceding the emergence of SBD.Through the analysis of the norm(N),we further unveil that the interplay between the non-Hermitian driving potential and the nonlinear interaction underlies the SBD phenomenon.

The paper is structured as follows: In Section 2, we present the QPQKR model of BEC, incorporating nonlinearity and non-Hermiticity.In Section 3,we explore the diffusion behavior within this system,focusing particularly on the SBD behavior, and discuss its underlying mechanism.A summary is presented in Section 4.

2.Theoretical model

We consider a system of ultra-cold atoms confined in a ring trap with radius ofRand subjected to quasi-periodicδkicks of optical standing wave with complex dielectric constants.[47–49]The Hamiltonian of the QPQKR model reads

with the quasi-periodic kicking potential

whereθis the angle coordinate.We take ?p=-iˉheff?/?θas the corresponding angular momentum operator, with ˉheffbeing the effective Planck constant and satisfying the commutation relation [θ, ?p]=iˉheff.The nonlinear interaction strength is denoted byg, whileKandλcontrol the strength of the real and imaginary parts of the kicking, respectively.Additionally,εis the quasi-periodic modulation strength for the kicking potential.When the modulation frequency is incommensurable with the kicking frequency,ensured byω=2πr/swithrandsbeing coprime numbers, the QPQKR model can mimic the 2D Anderson model.[20,21]Here,ω=2πe.All variables are scaled to dimensionless units.It is worth noting that the QPQKR model in the Hermitian case(i.e.,λ=0)has been utilized to demonstrate the nonlinearity induced sub-diffusion of energy.[20,21]

where the free evolution operator is defined as

the evolution operator of the kicking term is defined as

and the nonlinear interaction reads

whereβis the diffusion coefficient.Interestingly, the system displays a wide spectrum of energy diffusion from the SBD withα ＞2,to AD with 1＜α ＜2 and CD withα=1,with the increase of the nonlinearity parameterg.Our finding provides new insights into the chaotic dynamics of quantum many-body systems and opens up avenues for further research on the fundamental problems,e.g.,quantum thermalization in this field.

Fig.1.Schematic phase diagram of quantum diffusion (〈p2〉∝tα) in the parameter space(λ,g).The solid curve of λc denotes the crossover from diffusion phase with interplay between nonlinear interaction and non-Hermitian driving to diffusion phase without interplay.The three dashed lines indicate nonsingular crossover between different diffusion phases with variation of nonlinear interaction.Here gc denotes the threshold of nonlinear interaction strength for the crossover from phase I to phase II.It is slightly dependent on λ.

3.Super-ballistic quantum diffusion induced by nonlinear interaction

3.1.Time dependence of mean energy and inverse participation ratio

We numerically investigate the time-dependent mean energy〈p2〉 for various values ofg, specifically in cases where the non-Hermitian driving potential is sufficiently large.We initialize the system in the ground state, represented asAs depicted in Fig.2(a), wheng= 0,the energy diffusion〈p2〉 exhibits DL, which is induced by non-Hermiticity.[45]The corresponding momentum distribution has an exponentially localized shape,|ψ(p)|2∝e-|p|/μ[see Fig.2(d)], which is a typical characteristic of DL.For weak nonlinearity (e.g.,g=10-3), the mean energy follows the DL ofg=0 for time smaller than a threshold valueκc,representing the occurrence of prethermalization.Interestingly,fort ＞κc, quantum diffusion displays the way of SBD, i.e.,〈p2〉=βtαwithα ≈3.3.

We observe that the exponentαdecreases asgincreases,following the relationα∝-lng, as illustrated in Fig.2(c).This relationship suggests a transition in the diffusion from SBD to AD and then to CD, as demonstrated in Fig.1.Furthermore, we numerically explore the growth rateβacross a wide range ofgvalues.Our findings indicate thatβincreases according to a power law withg, i.e.,β∝gγ, as shown in Fig.2(c).This result reveals an enhancement of diffusion due to nonlinear interaction.In this situation,the probability density distribution in momentum space can be expressed as

This distribution displays a plateau for|p|＜pcand exponentially decaying tails for|p|＞pc[see Fig.2(d)].The width of the plateau,represented byL(t)=2pc(t),increases with time,signifying the emergence of delocalization.[50,51]

Fig.2.Time evolution of〈p2〉(a),and ξ (b)with g=0(black),10-3(cyan), 10(blue), and 50(green).Red lines in panels(a)and(b)indicate〈p2〉=βtα and ξ ∝tα/2,respectively;κc in panel(a)is the critical time of the pre-thermalization.(c)Dependence of α (triangles) and β(circles)on g.The red solid(dashed)line indicates the fitting function with the form α ∝-lng (β ∝gγ with γ =2.3).(d) Angular momentum distributions |ψ(p)|2 at time t =2×104 for g=0 (circles) and g=10 (triangles).The green (red) line indicates the fitting function|ψ(p)|2 ∝e-|p|/μ for g=0[Eq.(8)for g=10].Other parameters are K=5, ˉheff=5,ε =0.1,and λ =10-2.

The inverse participation ratio (IPR) has been widely used to assess the spread of a quantum state and is represented by the equationξ=(∑m|ψm|2)2/∑m|ψm|4, withm=...,-2,-1,0,1,2,....[45,52,53]We further investigate the IPR(ξ) for various values ofg.Figure 2(b) shows that the IPR rapidly increases and reaches saturation wheng=0.It can be readily deduced that the IPR is proportional to the localization lengthμfor an exponentially localized quantum state given by|ψ(p)|2∝e-|p|/μ.Notably, the IPR follows a power-law growth with time, i.e.,ξ∝tα/2for nonzerog.Here,αrepresents the exponent of diffusion for the〈p2〉.The relationship betweenξand〈p2〉 can be determined using the probability density distribution provided in Eq.(8).By disregarding the exponentially decaying tails, a rough estimation ofρcorresponding to the plateau of the momentum distribution in Eq.(8) givesρ∝1/pc, resulting from normalization.Consequently, we establish the relation〈p2〉～ξ2, which unveils the correlation between the spread of the quantum state and energy diffusion.

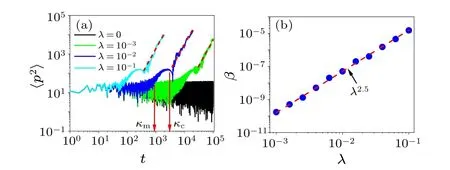
Fig.3.(a) Time evolution of 〈p2〉 for different λ.Red dashed lines indicate the fitting function with the form〈p2〉=βt2.7; κm and κc are critical times of pre-thermalization.(b) Dependence of β on λ.The red dashed line indicates the fitting function of the form β ∝λν with ν =2.5.Other parameters are K=5, ˉheff=5,ε =0.1,and g=0.1.

We further investigate the time evolution of〈p2〉for various values of the parameterλ.In the Hermitian case (i.e.,whenλ= 0), the energy diffusion exhibits DL, as shown in Fig.3(a).For a sufficiently strong non-Hermiticity (e.g.,λ=10-3), the〈p2〉follows the DL ofλ=0 fort ＜κm, exhibits a type of prethermalization in the time intervalκm＜t ＜κc,[54,55]and ultimately increases with an SBD of timet,that is,〈p2〉=βtα,where the exponentαremains constant asλvaries.The diffusive coefficientβincreases according to a power function,specifically,β∝λνwithν=2.5,as depicted in Fig.3(b).This demonstrates the enhancement of diffusion by the non-Hermitian driving potential.

3.2.Mechanism of super-ballistic diffusion

To reveal the mechanism of super-ballistic diffusion, we examine the normNof the quantum state in time evolution for various values ofλandg.The norm can be used to quantify phase transitions in non-Hermitian systems.[43,56]In the Hermitian system [i.e.,λ=0 andg=0.1 in Fig.4(a)], theNremains at unity throughout the time evolution, demonstrating the conservation of the norm.Correspondingly, the mean energy exhibits DL, as depicted in Fig.3(a).In the non-Hermitian system without nonlinear interaction[e.g.,λ=10-2andg=0 in Fig.4(a)], the norm decreases slightly for time smaller a threshold valuetm, beyond which it increases sharply in an exponential function,i.e.,N∝eηt.We numerically investigate thetmfor differentλ.Figure 4(c) demonstrates thattm, in perfect consistency with the threshold timeκmfor the DL of energy diffusion, decays inversely withλ.This demonstrates that the DL exists prior to the manifestation of non-Hermitian effects.

For nonzerogvalues (e.g.,g=0.1 in Fig.4(b)),Nfollows the behavior ofg=0 for times smaller than a threshold valuetc.Beyond this point,it also increases unboundedly,but at a significantly lower rate compared to the case ofg=0.We further investigate thetcfor differentg.Figure 4(d) reveals thattcdecays logarithmically withg, i.e.,tc∝-lng, which is in good agreement with the behavior of threshold timeκcfor the appearance of the SBD.This demonstrates that the effects of nonlinear interaction becomes predominant fort ＞tc,leading to the occurrence of the SBD.

Fig.4.(a)Norm(N)versus time for g=0.1 with different λ and g=0 with different λ.Red dashed lines indicate the fitting function of the form N ∝eηt.(b) Norm (N) versus time for λ =10-2 with g=0(black),10-5 (gray),10-3 (cyan),0.1(olive),1(green),10(magenta),and 50(blue).Here tm and tc in panels(a)and(b)are critical points of N.(c)Dependence of κm and tm on λ for g=0.1.(d)Dependence of κc and tc on g for λ =10-2.Red dashed lines in panels (b), (c), and(d)indicate the fitting function of the form N ∝eηt with η =0.0027,tm(κm)∝1/λ, and tc(κc)∝-lng, respectively.Other parameters are K=5, ˉheff=5,and ε =0.1.

4.Summary

We numerically identify several energy diffusion behaviors in the parameter space (λ,g) using the QPQKR model forλ ＞λc, specifically, SBD, AD, and CD.The mean energy adheres to a power-law function of time, represented by〈p2〉=βtα,α ≥1.The diffusion exponentαdecreases logarithmically withg,while the diffusion coefficientβincreases with a power law regardingg.Interestingly, the system experiences a prethermalization stage before transition to SBD.The time evolution of the normNdisplays two critical times,tmandtc, which are consistent with the threshold time ofκmof DL andκcof SBD, respectively.We find that thetm(κm)decays inversely withλ, whiletc(κc) decays logarithmically withg.Our analysis ofNdemonstrates that the interplay between the non-Hermitian driving potential and the nonlinear interaction results in the emergence of SBD.

Appendix A: Experimental design and nondimensionalization for the BEC system

We introduce a nonlinear interaction in momentum space,i.e.,VNL= ˉg|ψ(P)|2.[32]The Hamiltonian of the BEC system considered in this work is given by

with

Acknowledgments

Jian-Zheng Li is supported by the Science and Technology Research Program of Jiangxi Education Department (Grant No.GJJ190463) and the Doctoral Startup Fund of Jiangxi University of Science and Technology (Grant No.205200100067).Wen-Lei Zhao is supported by the National Natural Science Foundation of China (Grant No.12065009), the Natural Science Foundation of Jiangxi Province (Grant Nos.20224ACB201006 and 20224BAB201023),and the Science and Technology Planning Project of Ganzhou City(Grant No.202101095077).