Breather,lump,and interaction solutions to a nonlocal KP system
Quanyong Zhu,Lijun Xu,Jinxi Fei,Huiling Wu and Zhengyi Ma,4
1 Institute of Nonlinear Analysis and Department of Mathematics,Lishui University,Lishui 323000,China
2 Faculty of Preschool Teacher Education,Lishui University,Songyang 323400,China
3 Institute of Optoelectronic Technology and Department of Photoelectric Engineering,Lishui University,Lishui 323000,China
4 Department of Mathematics,Zhejiang Sci-Tech University,Hangzhou 310038,China
Abstract
A new high-dimensional two-place Alice-Bob-Kadomtsev-Petviashvili (AB-KP) equation is proposed by applying the Alice-Bob-Bob-Alice principle and shifted-parity,delayed time reversal,charge conjugationprinciple to the usual KP equation.Based on the dependent variable transformation,the bilinear form of the AB-KP system is constructed.Explicit trigonometric-hyperbolic,rational and rational-hyperbolic solutions are presented by taking advantage of the Hirota bilinear method.The obtained breather,lump,and interaction solutions enrich the solution structure of nonlocal nonlinear systems.The three-dimensional graphs of these nonlinear wave solutions are demonstrated by choosing the specific parameters.
Keywords: AB-KP equation,bilinear method,breather solution,lump solution,interaction solution
1.Introduction
The pioneering application of the Korteweg-de Vries (KdV)formula for the propagation velocity of a soliton to two problems by John Scott and Russell,the discovery by Boussinesq,Korteweg,and de Vries of the first formulation of model equations to describe a soliton stand as two of the most important developments in modern nonlinear science.As a prototypical completely integrable system,the KdV equation has had a tremendous impact on many active fields of pure mathematics,physical sciences,and the fields in between [1,2].The KdV equation also has important applications in other famous integrable equations,including the nonlinear Schr?dinger equation (NLS) and the sine-Gordon equation (SG) [3,4].
Applications for these celebrated integrable systems include nonlinear optics in Kerr media,condensed matter physics,fluid mechanics,semiconductor physics,electromagnetics,laser physics,hydrodynamics,lattice dynamics and plasma physics [5-11].There are also many continuous and discrete integrable evolution partial differential equations (PDEs) that are physically significant and apply to a plethora of situations.Recently,a novel integrable nonlinear evolution PDE,namely,the nonlocal NLS equation,was discovered from the reduction of the Ablowitz-Kaup-Newell-Segue(AKNS)hierarchy[12].Soon afterwards,other types of integrable nonlocal evolution PDEs have been constructed,such as integrable nonlocal KdV type equations,nonlocal Sine/Sinh-Gordon equations,and couple nonlocal NLS equations [13-15].Enlightened by these findings,there is great interest in the field of integrable nonlocal parity-time (PT) symmetric systems in mathematical physics societies.A profusion of other unusual properties has also been reported in integrable nonlocal PT-symmetric systems.Meanwhile,there are other intrinsic properties in physics,such as charge conjugation,shifted parityand delayed time reversaland their cross combinations,such as,,,and,that can be employed to model two or more place physical problems.These systems are called Alice-Bob (AB) systems submitted to the AB-BA (Alice-Bob-Bob-Alice) principle and theprinciple [16,17].To obtain concrete results,various systematic machineries have been proposed to construct explicit solutions for nonlocal nonlinear PDEs.For example,the inverse scattering transform method,the Hirota bilinear method,the Riemann-Hilbert approach,the variable separation method,the B?cklund transformation method,and the symmetry reduction method.These methods have been widely sharpened in the last few years,e.g.,see [18-30] and the references therein.Since most of the nonlinear PDEs of physically significant are written in high dimensions,whether these equations can be integrated is a question of fundamental importance.Shi et al obtained mixed lump-soliton solutions for the extended highdimensional Nizhnik-Novikov-Veselov equation using the Hirota bilinear method [31].Wei et al derived soliton molecules and multi-breather solutions for the high-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation [32].
In this work,the construction problem of coherent structures to a high-dimensional,nonlocal,and nonlinear system,i.e.,the high-dimensional Alice-Bob-Kadomtsev-Petviashvili (AB-KP) equation,is treated.The considered system is given by
where
At=etc,α,β,σ and γ are arbitrary constants.Historically,the KP equation has received intensive interest and is one of the best-known integrable multi-dimensional systems.As a universal model,a wide variety of physically significant problems arising in very different areas(e.g.,plasma physics,water waves,and internal waves) are described by the KP equation.Many methods have been proposed for search analytical solutions of the KP equation,such as the Darboux transformation method [33],the long wave limit approach[34],and the Hirota bilinear method [35].
This paper is arranged as follows.In section 2,we first construct the high-dimensional AB-KP system via AB-BA and theprinciple.The bilinear form of the AB-KP system is then deduced according to the Hirota method.A breather solution is obtained with the help of a variable transformation technique.In section 3,the rational lump solution to the AB-KP system is obtained by taking the auxiliary function as a quadratic function.Furthermore,the interaction between a lump and a pair of solitons of the ABKP system is illustrated in section 4.Finally,we give our conclusions in section 5.
2.Breather solution to the AB-KP equation
The high-dimensional AB-KP equation (1) is established according toprinciples.By substituting the symmetricu=into the classical high-dimensional KP equation
we have
equation (3) can be split into the following two equations
where G(A,B)is an arbitrary function of A and B.B is related to A under theprinciple,i.e.,B==A(?x+x0,?y+y0,?z+z0,?t+t0),where P and T are parity transformation and time reversal operators,respectively.It is easy to find that if B is far from A,then the AB-KP equation is nonlocal.Without loss of generality,G(A,B) is fixed to zero,then equation (4) can be reduced to the following system
It is clear that equations 5(a) and (b) are equivalent to the following equation
Inspired by Bell polynomial theories,we introduce the dependent variable transformation as follows
where a is an arbitrary constant.Transformation (7) is an ordinary B?cklund transformation with a=0.By substituting transformation (7) into equation (5),the bilinear form of the AB-KP system can be derived as follows
whereDxDt,Dx4and D2yare the Hirota bilinear derivative operators defined by
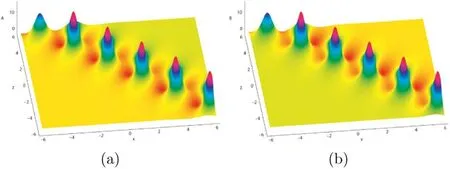
Figure 1.The exhibition of the breather solution with t=0,y=1: (a) solution (15); (b) solution (16).
The bilinear form of the AB-KP system (8) can be rewritten as follows
It is well-known that a class of breather solutions to the classical KP equation can be obtained via the general technique.In order to search for breather solutions to the highdimensional AB-KP equation,the auxiliary function f can be written as
Then noticing the variable transformation (7),a breather solution of the AB-KP system (6) may be expressed as

3.Lump solution
In this section,we will inquire into rational solutions of the AB-KP system in detail and show that equation(6)has a lump solution,decaying in all directions.By applying the Taylor expansion technique to equation (11) at ?=0 with b1=1+a9?2,b2=?2,(b3,b4)=(?,?),one obtains the quadratic auxiliary function f,which can be expressed as
where
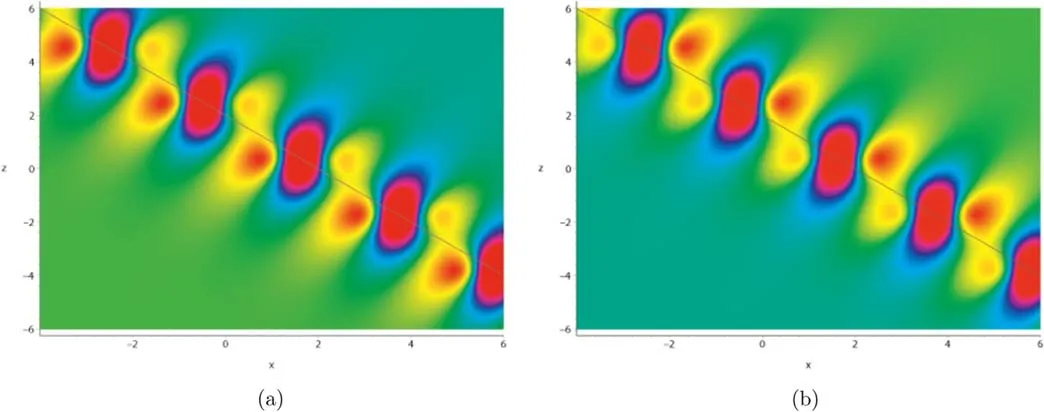
Figure 2.The density plots of the breather solution with t=0,y=1: (a) solution (15); (b) solution (16).
By inserting (17) into (10) directly,one can deduce the following constraint conditions
By virtue of the variable transformation (7),a lump solution of the system (5) can be obtained as follows:
where
Analyzing the local properties of (21) where the first derivatives equal to zero yields the maximum amplitude
Further calculation shows that the lump solution moving with the velocities
and along the path
which is derived from
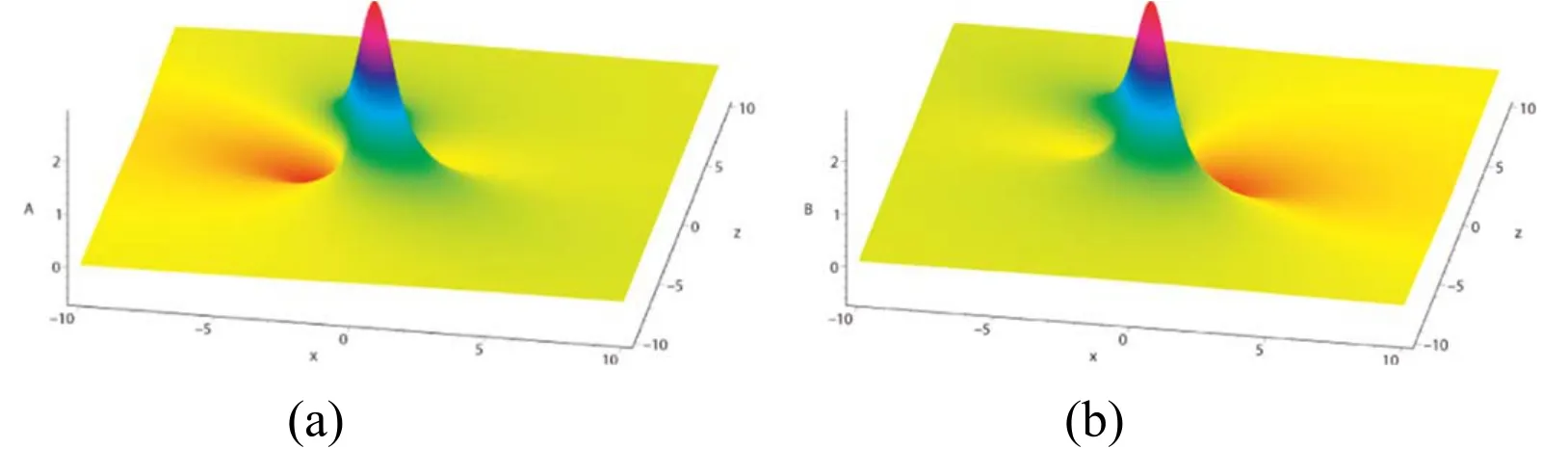
Figure 3.The exhibition of the lump solution (21) with (20) when t=0,y=1: (a) the profile of the lump (21a); (b) the profile of the lump (21b).
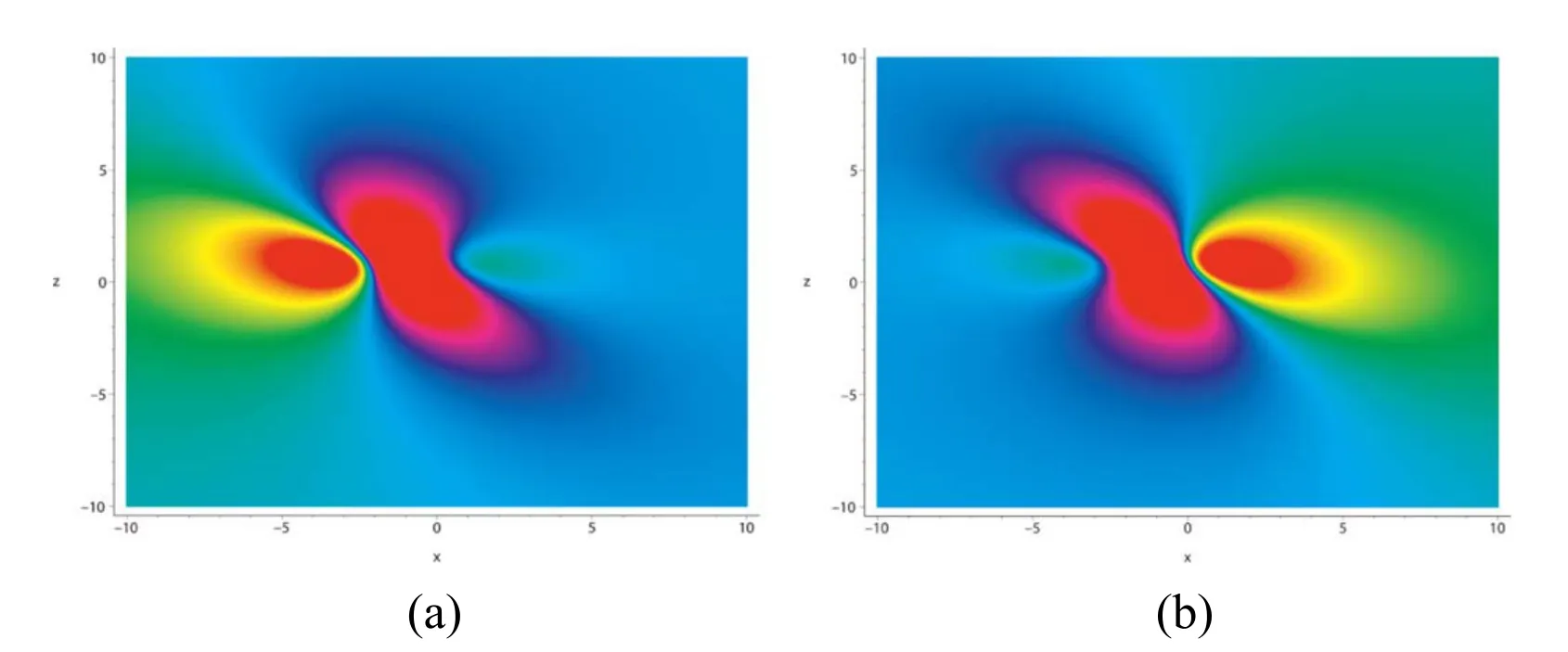
Figure 4.The density plots of the lump solution (21) with (20) when t=0,y=1: (a) the lump (21a); (b) the lump (21b).
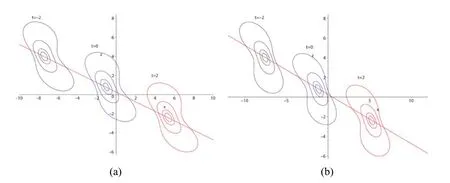
Figure 5.The contour curves of the lump solution (21) with (20) when t=?2,0,2,y=1:(a) the lump (21a); (b) the lump (21b).
In figures 3,4,and 5,the lump solution (21) is drawn for a particular choice of parameters a1=?1/2,a2=a3=a5=a6=a7=x0=y0=z0=t0=α=1,β=2,and σ=γ=I(I2=?1).Figures 3(a)and 3(b)show the three-dimensional profiles of the lump (21a) and (21b) when t=0,y=1,respectively.Figures 4(a)and 4(b)depict the density plots of the lump(21a)and(21b)when t=0,y=1,respectively.The contour curves with different values of variable t when y=1 are drawn in figures 5(a) and (b).One can observe that these lumps evolve along the line z=?x/2+1/4.
4.Interaction of one lump with a pair of solitons
In this section,we will study the interaction solution consisting of one lump and a pair of solitons for the AB-KP system(6).To this end,the auxiliary function f is assumed as a combination of rational function and hyperbolic function,from which we will obtain the hybrid lump-soliton solution.More precisely,f can be concisely written in terms of rationalhyperbolic form

Figure 6.The exhibition of interaction between a lump and a pair of solitons by(34a)with(32).(a)t=?20;(b)t=?5;(c)t=0;(d)t=5;and (e) t=20.
with
where ai(i=1,2,…,8),c0,and c1are real undetermined parameters.We can use(28)and(10)to solve for these undetermined parameters.Upon doing some symbolic computation,the constraints on the undetermined parameters can be written as
with
Since the real parameters are given by(32),we have deduced the following interaction solution between one lump and a pair of solitons of the AB-KP system (5)
The propagation process of the interaction solution between one lump and a pair of solitons(34a)is depicted in figure 6 with the specific parameters a=0.5,a1=?0.5,b1=0.1,a2=a3=a5=a6=a7=x0=y0=z0=t0=1,and α=1,β=2,γ=σ=I,y=1.It can be seen that there only exists a pair of solitons at first,a lump and two solitons coexist later,and as time goes on the lump is induced by the soliton on the righthand hand side gradually,it then splits into a lump and a soliton.The lump is induced by the soliton on the left-hand side when the value of t keeps varying,it then splits into a lump and a soliton again.
5.Conclusions
In summary,we derived explicit trigonometric-hyperbolic,rational,and rational-hyperbolic solutions of the highdimensional AB-KP system.The bilinear form of the AB-KP system is derived by introducing a suitable dependent variable transformation.Mixed trigonometric-hyperbolic,purely rational,and mixed rational-hyperbolic solutions are obtained by setting the auxiliary function as the combination of trigonometric and hyperbolic functions,quadratic function,and the combination of quadratic and hyperbolic functions.The mixed trigonometric-hyperbolic solution corresponds to a breather soliton that oscillates periodically in duration and amplitude.The rational function solution represents one lump that is a local wave with a uniform state in all directions in space.The mixed rational-hyperbolic solution depicts the interaction of one lump with two solitons.The local feature and interactive nature of these nonlinear wave solutions are presented analytically in detail.Furthermore,the threedimensional graphs of these nonlinear wave solutions are demonstrated.The obtained nonlinear wave solutions enrich the solution structure of two-place nonlocal systems.The established direct method is simple and it can be expected to explore more novel physically meaningful solutions of nonlocal nonlinear systems.
Acknowledgments
We would like to express our sincere thanks to Dr Junchao Chen for his valuable comments.This work was supported by the National Natural Science Foundation of China under grant number 11 447 017.
ORCID iDs
 Communications in Theoretical Physics2023年7期
Communications in Theoretical Physics2023年7期
- Communications in Theoretical Physics的其它文章
- Dynamic magnetic behaviors and magnetocaloric effect of the Kagome lattice:Monte Carlo simulations
- Electrical properties of a generalized 2 × n resistor network
- Unsteady detonation with thermodynamic nonequilibrium effect based on the kinetic theory
- The performance of a dissipative electrooptomechanical system using the Caldirola-Kanai Hamiltonian approach
- LitePIG: a lite parameter inference system for the gravitational wave in the millihertz band
- Cosmic acceleration with bulk viscosity in an anisotropic f(R,Lm) background
