Searching For (2+1)-dimensional nonlinear Boussinesq equation from (1+1)-dimensional nonlinear Boussinesq equation
Man Jia and S Y Lou
School of Physical Science and Technology,Ningbo University,Ningbo,315211,China
Abstract
A novel(2+1)-dimensional nonlinear Boussinesq equation is derived from a(1+1)-dimensional Boussinesq equation in nonlinear Schr?dinger type based on a deformation algorithm.The integrability of the obtained (2+1)-dimensional Boussinesq equation is guaranteed by its Lax pair obtained directly from the Lax pair of the(1+1)-dimensional Boussinesq equation.Because of the effects of the deformation,the (2+1)-dimensional Boussinesq equation admits a special travelling wave solution with a shape that can be deformed to be asymmetric and/or multivalued.
Keywords: (2+1)-dimensional Boussinesq equation,deformation algorithm,lax integrable,an implicit travelling wave solution
Searching for higher-dimensional physical models is important and challenging in all branches of physics.In order to precisely describe the real(3+1)-dimensional physical space,many higher dimensional systems have been explored by various physicists and mathematicians.However,due to the complexity and difficulty,higher models are traditionally reduced to lower-dimensional ones to simplify the calculations and illustrate the general rules.For example,using the classical and nonclassical Lie approaches [1] to reduce a nonlinear partial differential equation(PDE)to some ordinary differential equation is one of the most effective ways of solving a nonlinear PDE.
Since the simplification of higher dimensional models to lower dimensional ones is popular and successful,it is interesting to consider the problem if it were possible to search for the higher dimensional systems from lower ones.This process is naturally more difficult.Fortunately,it is possible that some higher dimensional systems can be constructed from the lowers ones.For instance,some nontrivial(3+1)-dimensional integrable models can be constructed from the (2+1)-dimensional Kadomtsev-Petviashvili (KP),nonlinear Schr?dinger (NLS),and Schwarz Korteweg-de Vries(KdV) equations [2] via Painlevé analysis.The famous(1+1)-and (2+1)-dimensional sine-Gordon equations and Tzitzeca equations can be obtained from the (0+1)-dimensional Riccati equation [3].
Recently,in order to obtain more high-dimensional integrable systems in some traditional integrable meanings,a deformation algorithm [4] is proposed,which enables arbitrary lower-dimensional integrable systems to be deformed into high-dimensional ones.
Deformation algorithm 1.For a general (1+1)-dimensional integrable local evolution system
if there exist some conservation laws
where the conserved densitiesρiare dependent only on the field u while the flows Jican be field derivative dependent,then the deformedD+1-dimensional system
may be integrable with the deformation operators
and the deformed flows
The correctness of the deformation algorithm (or the deformation conjecture) has been checked by the authors of[4] for almost all the known local integrable evolution systems.It is found that the new high dimensional integrable systems obtained from the deformation algorithm possess completely different structures and properties from the traditional integrable systems.Although the new models possess elegant properties,such as the existence of the Lax pair and the infinitely many symmetries,the traditional research methods of integrable systems can no longer be successfully applied because the original models and their several reciprocal systems are included in the same models.
The(1+1)-dimensional Boussinesq equation,considered as the first model for nonlinear dispersive wave propagation,was obtained by Boussinesq in his study of long water waves[5].Later,the Boussinesq equation was independently considered by Zakharov [6] in studying one-dimensional chains of nonlinear oscillators,Kruskal and Zabusky in their study of one Fermi-Pasta-Ulam problem [7],and Ablowitz and Haberman in higher order matrix eigenvalue problem[8].The well-known KdV equation can be derived from the Boussinesq equation with the wave motion being restricted to be unidirectional.The Boussinesq equation is proved to be Lax integrable and solvable via the inverse scattering method,possessing the bilinear form and N-soliton solutions [9].Recently,the Boussinesq equation is extended to the different types of nonlocal Boussinesq systems by[10]via the parity or time-reversal symmetry reduction,[11,12].It is interesting that the nonlocal Boussinesq systems exhibit different properties for the prohibitions [10],symmetry-breaking solutions and bright and dark soliton solutions [11] caused by nonlocalities.Furthermore,the Boussinesq equation in fractional type is also derived in [13] and exact solutions are found to describe fractal domains.
Though many higher dimensional Boussinesq equations have been constructed by various authors,such as the(2+1)-dimensional Boussinesq equations describing the propagation of gravity waves on the surface of water [14-16] and the(3+1)-dimensional Boussinesq equations in [17,18],the obtained higher dimensional Boussinesq equation is generally related to the known KP equation up to the scaling and exchange of y and t [19].Some of the (2+1)-dimensional Boussinesq equations are not in the classes of completely integrable equations [14,18,20].
Because the Boussinesq equation is widely used in fluid dynamics and possesses properties different from other integrable systems in nonlinear science,it is necessary to extend the lower dimensional Boussinesq equation to the higher dimensional models different from the known integrable systems.In this manuscript,we devote our search to finding various higher dimensional Boussinesq equations using the deformation algorithm.
We start from the (1+1)-dimensional Boussinesq equation written in NLS type [19],say
It is easy to check the (1+1)-dimensional Boussinesq equation (6) is Lax integrable with the Lax pair
From equation (6),it is not difficult to find the Boussinesq equation possesses a type of conservation law
with the conserved density ρ=α+β and conserved flow J=αx?βx.Thus,by applying the deformation algorithm to the Boussinesq equation (6) with the deformation operators
where the deformed flow is defined as
a particular (2+1)-dimensional Boussinesq equation is successfully derived
i.e.,
The integrability of the (2+1)-dimensional Boussinesq equation (12) is guaranteed by the Lax pair,say,
which can be directly obtained from the Lax pair of the(1+1)-dimensional Boussinesq equation by applying the deformation algorithm.The compatibility condition of equation (13) for
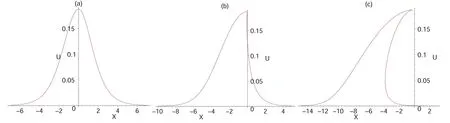
Figure 1.The implicit solution U given by equation (19),with k=1/2,ω=1/4,and p=1/5 in (a),p=3 in (b) and p=10 in (c),respectively.
yields the (2+1)-dimensional Boussinesq equation (12).
To investigate the properties of the obtained integrable system equation (12),we seek the travelling wave solution structures for this model.One can easily check the (2+1)-dimensional Boussinesq equation (12) has the following travelling wave solution
where the constants k,p and ω are arbitrary constants.
It is known the solution of equation (17) can be expressed by the following elliptic integral
where c2and X0are two arbitrary integral constants.With suitable parameters selections,the travelling wave solution for equation (18) is implicitly obtained by
Thus,the exact travelling wave solution for the new(2+1)-dimensional Boussinesq equation (12) is
where A and U are constrained by equation (16) and U is implicitly given by equation (19).
Though the travelling wave solution equation (20) can not be expressed analytically and explicitly,we can really find the solution is different from the traditional integrable systems before.The special solution U is displayed in figure 1 with the same parameters selections for k and ω and various values for p.It is discovered as p increases,the soliton shape will deform to an asymmetric soliton and a foldon or folded solitary wave(multi-valued soliton or solitary wave [21]).
In conclusion,we establish a (2+1)-dimensional Boussinesq equation from the (1+1)-dimensional Boussinesq equation in NLS type via a deformation algorithm.This type of Boussinesq equation is discussed here because it has the special conservation law with the conserved density ρ dependent on α and β and the flow J dependent on αxand βx.By applying the algorithm to the Lax pair of the (1+1)-dimensional Boussinesq equation,the Lax pair of the newly obtained (2+1)-dimensional Boussinesq equation is constructed.The travelling wave solutions of the (2+1)-dimensional Boussinesq equation are expressed by a complicated elliptic integral equation (18) and a constraint ordinary differential equation (16).Because of the effects of the deformation,it is very difficult to find analytical explicit solutions of the obtained (2+1)-dimensional Boussinesq equation.
Though the deformation algorithm has been applied to many known integrable systems and has been successfully used to find higher-dimensional ones,it is still difficult to search for higherdimensional discrete integrable systems.New methods and progresses should be explored for the discrete integrable systems.
Acknowledgments
The authors acknowledge the support of the National Natural Science Foundation of China (Nos.12275144,12235007 and 11975131)and the K C Wong Magna Fund at Ningbo University.
ORCID iDs
 Communications in Theoretical Physics2023年7期
Communications in Theoretical Physics2023年7期
- Communications in Theoretical Physics的其它文章
- Dynamic magnetic behaviors and magnetocaloric effect of the Kagome lattice:Monte Carlo simulations
- Electrical properties of a generalized 2 × n resistor network
- Unsteady detonation with thermodynamic nonequilibrium effect based on the kinetic theory
- The performance of a dissipative electrooptomechanical system using the Caldirola-Kanai Hamiltonian approach
- LitePIG: a lite parameter inference system for the gravitational wave in the millihertz band
- Cosmic acceleration with bulk viscosity in an anisotropic f(R,Lm) background
