Tong Liu(劉通) and Shujie Cheng(成書杰)

1School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Department of Physics,Zhejiang Normal University,Jinhua 321004,China

Keywords: non-Hermitian,quasiperiodic,mobility edge

1.Introduction

The unavoidable exchange of the particles, energy and quantum information with surrounding environment results in the open quantum systems.[1]From some insightful considerations, the quantum phenomena of these systems can be well described by the effective non-Hermitian Hamiltonians.[2]Due to the non-Hermiticity, the eigenvalues of systems generally become complex, which leads to the non-conservation of possibility.Nevertheless, if systems possess the paritytime (PT) symmetry, they may still have purely real energy spectra, and the presence of the real spectra implies that the gain and loss of systems are balanced.[3-5]The study of thePT-symmetry has been much active in the fields of quantum field theories,mathematical physics,[6]condensed matter physics,[7]and optical systems.[8]Thanks to the progress of the experimental technology, the gain and loss can be engineered controllably, which is beneficial to the observation of thePT-symmetry transition.[9]

On the other hand, the study of Anderson localization is quite an active field.Anderson localization refers to the breakdown of the diffusion of wave packets due to the disordered impurity.[10]One-dimensional lattice system is a customary platform to study the localization transition.A representative example is the Aubry-Andr′e (AA) model with quasiperiodic on-site potential, which represents the feature of the correlated disorder.[11]The AA model undergoes a delocalizationlocalization transition with the increasing strength of the quasiperiodic potential, and the phase transition point can be extracted by the self-dual condition.This localization transition has been observed in the bichromatic optical lattice of ultracold-atom experiments.[12]Since then,the AA model has drawn many theoretical and experimental researches.[13]

Recently, the interplay of the non-Hermiticity and the localization attracts a lot of research enthusiasm, such as the non-Hermitian Hatano-Nelson model with asymmetric hoppings[14]and the generalized non-Hermitian AA models.Gonget al.presented an intriguing topological explanation about the presence of the localization transition in the non-Hermitian Hatnano-Nelson model.[15]And Schifferet al.investigated a generalized AA model withPT-symmetry and uncovered thePT-symmetry protected localization phase.[16]

Nowadays, the combination of non-Hermiticity and the quasiperiodic potential has concentrated in the aspect of the non-Hermitian effect on the mobility edge.The physical concept of mobility edges was firstly proposed by Mott, based on the 3D Anderson model.The mobility edge refers to a critical energy separating localized from the extended states.Various AA-like models hosting mobility edges have been discussed, such as slow-varying potentials,[17]off-diagonal disorder,[18,19]long-range hoppings,[20]and other generalized quasiperiodic potentials.[21]Liuet al.[22]numerically found the simultaneous occurrence of the localization transition and thePT-symmetry breaking.Zenget al.[23]demonstrated the correspondence between the winding number and the localization transition, and numerically uncovered mobility edges in the spectrum with or without thePT-symmetry.And Liuet al.[24]uncovered the existence of the generalized Aubry-Andr′e self-dual symmetry and obtained the exactly analytical mobility edges in non-Hermitian quasicrystals.

However, to our best knowledge, the influence of non-Hermitian perturbations on the flatband lattice has not been studied.Flatband lattices[25]are translationally invariant tightbinding lattices which support at least one dispersionless band in the energy spectrum.Flatband systems have usually been considered as an ideal playground to explore the strong correlation phenomena as a result of the complete quenching of the kinetic energy of electrons.For example, a nearly flat band with non-trivial topology was proposed to simulate fractional Chern insulators.[26]The classification[25]through compact localized states (CLS) gives a good framework of the properties of flat bands, i.e., the numberUof unit cells occupied by a CLS.For theU=1 class, the CLSs form a set of orthogonal and complete bases,[25]indicating that a single CLS is disentangled from the rest of unit cells, such as the crossstitch network.However,for genericU＆gt;1 classes,the CLSs are not orthogonal to each other in one dimension,such as the sawtooth network.Taking into consideration of the exact solvability, not just limited to numerical simulation, in this work we focus on the study of the cross-stitch flatband lattice subjected to the non-Hermitian quasiperiodic perturbations.

2.Model and mobility edges

We consider a non-Hermitian cross-stitch lattice with the complex on-site potential

then we introduce two new physical quantities

and substitute them into Eq.(6),and eventually we obtain

It is known that a localization-delocalization transition[29]arises at the critical point ?V=±2 in Eq.(8).Thus the analytic expression is found for mobility edges of the non-Hermitian cross-stitch lattice

To support the analytical result given above, we now present detailed numerical analysis of Eq.(1).In the disordered system,the localization property of wave functions can be measured by the inverse participation ratio (IPR).[30]For any given normalized wave function, the corresponding IPR is defined as IPR=∑Ln=1|ψn|4,which measures the inverse of the number of sites being occupied by particles.It is well known that the IPR of an extended state scales likeL-1approaches to zero in the thermodynamic limit.However, for a localized state,since only finite number of sites are occupied,the IPR is finite even in the thermodynamic limit.In Fig.1,we show the IPR diagram in the[Re(E),V]plane, where different colors indicate different magnitudes of the IPR.The black eigenvalue curves denote the extended states, and the bright yellow eigenvalue curves denote the localized states.It is clearly demonstrating two mobility edges separating localized from extended states along the blue curves defined by Eq.(9).And the numerical results are in exact agreement with our theoretical predictions.

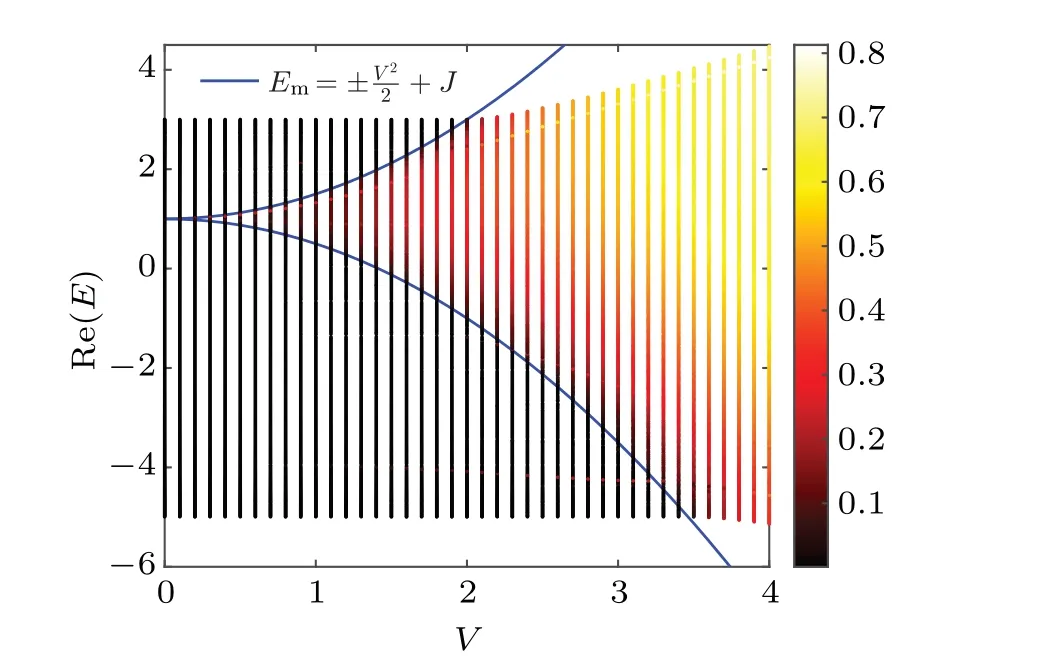
Fig.1.The real part of eigenvalues of Eq.(1) and IPR as a function of V with the parameter J =1.The total number of sites is set to be L=500.Different colors of the eigenvalue curves indicate different magnitudes of the IPR.The blue solid lines represent the boundary between spatially localized and extended states, i.e., the mobility edges Em=± +J.

3.Real-complex spectrum transition

Analyzing the energy spectrum, we find that there exists the real-complex transition of spectra, and mobility edges in this non-Hermitian model not only separate localized from extended states but also separate complex and real spectra.In Fig.2, we fix the size of the systemL= 500 and plot the eigenvalues of Eq.(1) with variousV.As Fig.2(a) shows,whenV=1,the eigenvalues outside the interval[0.5,1.5]are real and the system is in the extended phase, whereas those inside the interval [0.5,1.5] are complex and the system is in the localized phase.The critical energiesEmin=0.5 andEmax=1.5 are exactly corresponding to the mobility edgesThe results ofV= 1.5,V= 2 andV= 3 are also as expected, as shown in Figs.2(b), 2(c) and 2(d).Therefore, for each potential strengthV, we always find the separation of real and complex eigenvalues consistent with the exact solution to Eq.(9).The complex energy is accompanied with the localized state, whereas the real energy is accompanied with the extended state.We have also checked other combinations of parameters and get the same results as expected.Consequently, we find a perfect correspondence between the real-complex transition and the analytical mobility edge energy.

Fig.2.Real and imaginary part of eigenvalues for Eq.(1) with the parameter J=1 under open boundary conditions.(a)V =1,the imaginary part inside the interval[0.5, 1.5]is nonzero and eigenvalues form a closed curve,whereas the imaginary part outside the interval[0.5, 1.5]is zero and eigenvalues form a line.For other V’s,V =1.5(b),V =2(c) and V =3 (d), the same real-complex transitions of the spectrum occur.The blue solid lines represent the boundaries between the real and complex energy spectrum, which are in good agreement with the mobility edges Em =±+1.The total number of sites is set to be L=500.

This type of real-complex spectrum transition has nothing to do with thePTsymmetry, and it is a general phenomenon in disordered/quasiperiodic non-Hermitian systems.However, the underlying physical mechanism of this phenomenon remains unclear.In this paper,we try to give a qualitative explanation.

From Eq.(8), we can obtain all the information of the energy spectrum of this model.Reference [31] has demonstrated that the real-complex spectrum transition in this type of Hamiltonian equation is driven by the non-Hermitian disorder,rather than thePTsymmetry.Mathematically,according to Sarnak’s method,[32]the spectrum of Eq.(8)is governed by the Lyapunov exponentG(E).WhenG(E)＆gt;0,Eq.(8)has the dense spectrum,namely,the corresponding wave functions are localized;whileG(E)=0,the corresponding wave functions of Eq.(8) are extended, and the spectrum must be within the real number interval,not a complex number.

Consequently,a qualitative explanation for the correspondence of the real-complex spectra transition and the mobility edge separating the extended and localized states is that when the system is in the extended phase, the spectrum must be restricted to a real interval;[31]while the system is in the localized phase, the energy spectrum is not strictly restricted,generally in a complex number interval.Thus,we partially explain why the mobility edge coincides with the real-complex transition point.However,a complete explanation of this correspondence still need more deep-going researches.

4.Summary

In summary, we have studied the localizationdelocalization transition and the real-complex transition of the cross-stitch flatband lattice subject to the non-Hermitian quasiperiodic potentials.Firstly,we decouple the cross-stitch lattice and obtain the analytic form of mobility edges in the spectrum.Diagonalizing the Hamiltonian, we numerically obtain the eigenvalues and wave functions.The numerical results clearly show the existence of mobility edges and are in excellent agreement with the theoretical predictions.Furthermore,analyzing the energy spectrum,we demonstrate that mobility edges in this non-Hermitian model not only separate localized from extended states but also indicate the coexistence of real and complex eigenvalues.Our finding gives an example of the generation of mobility edges by the flatband lattice, and enriches the physical phenomena of low dimensional non-Hermitian quasiperiodic systems.

Acknowledgements

Project supported by the Natural Science Foundation of Jiangsu Province, China(Grant No.BK20200737), NUPTSF(Grant Nos.NY220090 and NY220208), the National Natural Science Foundation of China (Grant No.12074064),the Innovation Research Project of Jiangsu Province, China(Grant No.JSSCBS20210521), and China Postdoctoral Science Foundation(Grant No.2022M721693).