(School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China)

Abstract: The single-machine lot scheduling problem with splittable jobs to minimize the number of tardy jobs has been showed to be weakly NP-hard in the literature.In this paper,we show that a generalized version of this problem in which jobs have deadlines is strongly NP-hard,and also present the results of some related scheduling problems.

Keywords: Lot scheduling;The number of tardy jobs;Splitting jobs;Strongly NP-hard

§1.Introduction

The lot scheduling model has its origins in many applications such as the integrated circuit tests,the glue production with a heated container,the stone wash processing of textile products,and the digital advertisement display,etc (see [6,8,11]).The lot scheduling problem studied in this paper can be stated as follows.There arenavailable jobsJ1,J2,···,Jnto be processed on a single machine.Forj1,2,···,n,jobJjis associated with a sizesj ＞0,a due datedj ≥0 and a deadline≥dj.Each job is allowed to be split into two parts and processed in two consecutive lots.The machine handles one lot at a time without idle time and the total size of jobs in one lot cannot exceed its capacityc.Assume that all the parameterssj,dj,andcare positive integers withsj ≤c,and moreover,without loss of generality,assume that the processing times of both jobs and lots are unit.For a given schedule,let the completion timeCjof jobJjbe the time when it wholly finishes its processing.Specifically,CjkifJjis wholly in thek-th lot andCjk+1 ifJjis split into two parts with one part in thek-th lot and the other part in the (k+1)-th lot.For convenience,we call JobJj on-timeand setUj0 ifCj ≤dj,andtardyand setUj1 ifCj ＞dj.The objective of the problem is find a feasible schedule (subject to deadlines) with the minimum number of tardy jobs.Using the three-parameter notation of of Graham et al.[4],this scheduling problem can be denoted by 1|split,

Hou et al.[6] showed that the smallest-size-first rule optimally solves the single-machine problem with splittable jobs to minimize the total completion time.Yang et al.[9] showed that the counterpart,in which splitting jobs are not allowed,of the problem in Hou et al.[6]is strongly NP-hard,and proposed an integer programming algorithm and several heuristics.Zhang et al.[11] showed that the weighted smallest-size-first rule optimally solves the singlemachine problem with splittable jobs to minimize the total weighted completion time or the total weighted discount completion time.Chen et al.[2] further studied an extension in which the capacities of different lots may be not the same,and showed that the weighted smallest-size-first rule optimally solves the problem of minimizing the total weighted completion time or the total weighted discount completion time.Mor et al.[8] gave a polynomial algorithm for the single-machine problem with splittable jobs to minimize the number of tardy jobs,and showed that its counterpart with splitting jobs being not allowed is strongly NP-hard and presented an efficient heuristic.They also showed that the single-machine problem with splittable jobs to minimize the weighted number of tardy jobs is weakly NP-hard and devised a pseudo-polynomial time dynamic programming algorithm.In the related single-machine scheduling,Yuan [10]proved that the single-machine problem with deadlines to minimize the number of tardy jobs is strongly NP-hard.Chen et al.[1] proved that single-machine total late work problem with deadlines is strongly NP-hard.

The paper is organized as follows.In section 2,we describe the proof of strong NP-hardness.In section 3,we present some related results.

§2.NP-hard proof

We will show that problem 1|split,|∑Ujis strongly NP-hard by a polynomial reduction from the strongly NP-complete 3-Partition problem (see [3]).

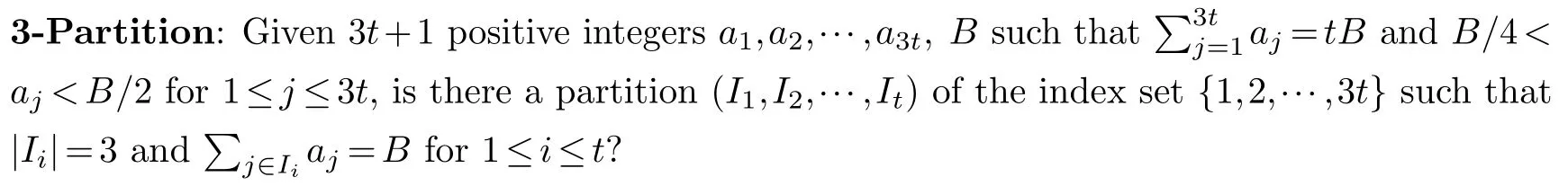
Let (a1,a2,···,a3t,B) be a given instance of 3-Partition.For our purpose,assume thata1≤a2≤···≤a3t.For the convenience of describing the job instance to be constructed,we first introduce the following parameters

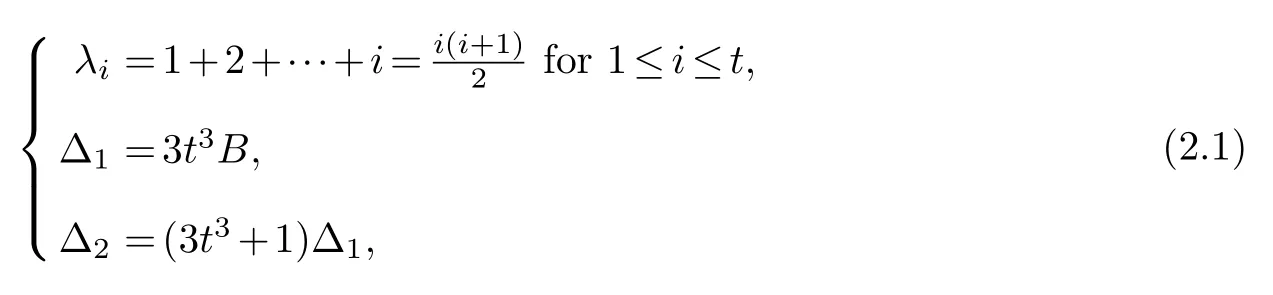
which satisfies

Table 1 The job instance.

The due date of each restricted job is equal to its deadline,i.e.,

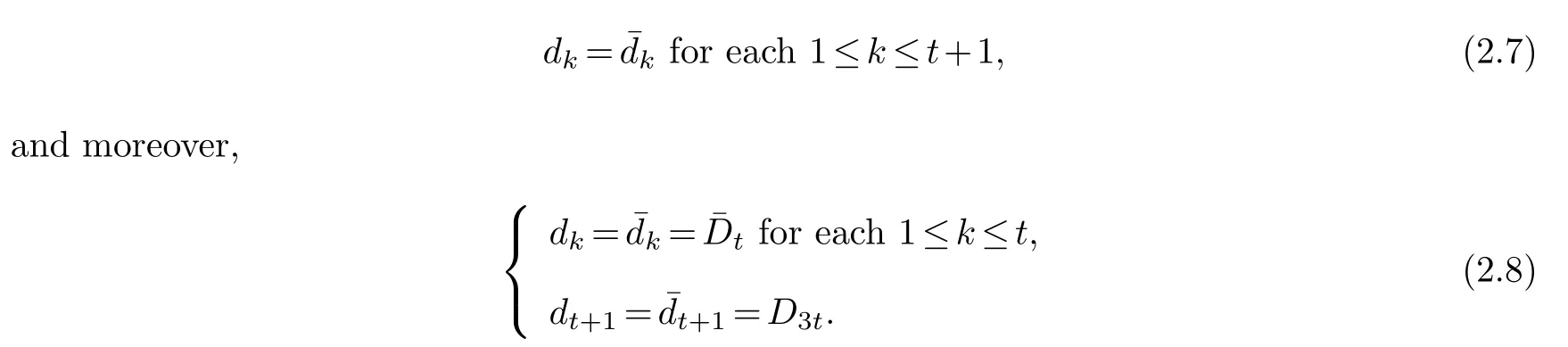
The following lemma connects a solution of the instance of 3-Partition and a desired subset of the job instance.

Lemma 2.1.The instance of 3-Partition has a solution iffthe above job instance has a desired subset.

Combing (2.10) and (2.17) yields

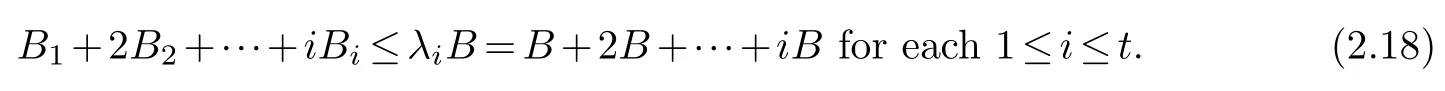
According to(2.16)and(2.18),we can showB1B2···BtBby the same technique in[10].This implies thatI1,I2,···,Itis exactly a solution of the instance of 3-Partition.Then the lemma follows.

Since the maximum due date of the normal jobs is 3t,the on-time normal jobs are scheduled in the first 3tlots.By (2.2),(2.4),(2.9) and (i),the total size of these on-time normal jobs is

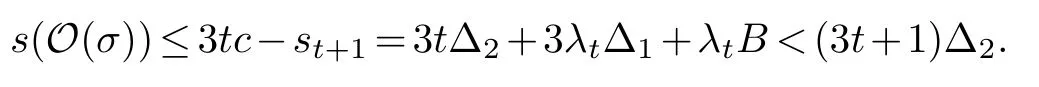
Considering that the size of each normal job is more than Δ2,we know that the number of the on-time normal jobs is no more than 3t.Then (ii) follows.

(iii) immediately follows from (i),(ii),and the fact of the number of jobs being 3t2+t+1.

According to (2.4) and (2.9),we further deduce

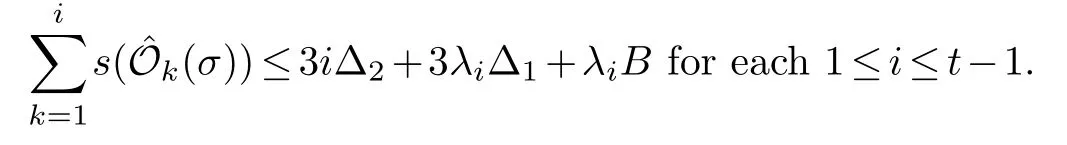
Then (iv) follows.

Based on Lemma 2.2,we can derive the following lemma which connects a desired subset and a desired schedule.

Lemma 2.3.The job instance has a feasible schedule such that the set of its on-time normal jobs is a desired subset,iffit has a desired schedule.

Proof.(?) Suppose thatσis a feasible schedule such that the setO(σ) of its on-time normal jobs is a desired subset.Then|O(σ)|3tby Definition 2.1.Together with Lemma 2.2(i) and the fact of the number of jobs being 3t2+t+1,we know thatσhas exactly 3t2-2t+1 tardy jobs,naturally showing thatσis a desired schedule.

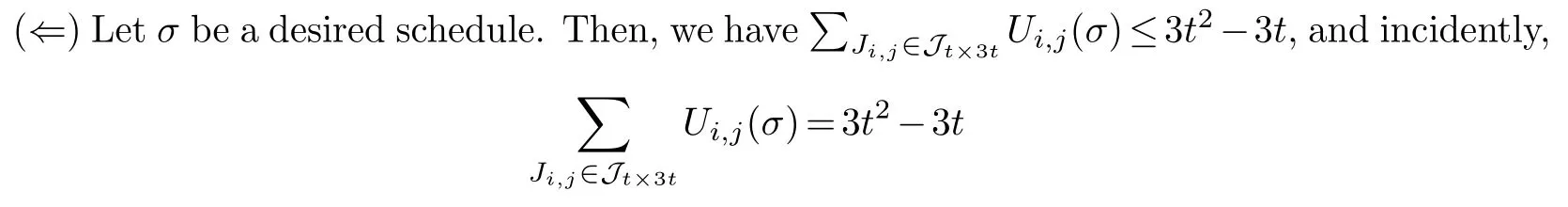
follows by Lemma 2.2 (iii).Moreover,according to Lemma 2.2 (i) and the fact of the number of jobs being 3t2+t+1 jobs,we can deduce that exactly 3tnormal jobs andt+1 restricted jobs are on-time,and all the other jobs are tardy inσ.Recall thatO(σ) denotes the set of the on-time normal jobs inσ.Then we have

By Lemma 2.2 (ii) and (iv),it also holds that

Henceforth,we use a permutation (Jσ(1),Jσ(2),···,Jσ(3t2+t+1)) of the 3t2+t+1 jobs to indicate the scheduleσ(it is reasonable since,given such a permutation,we can load the jobs in lots one by one and split a job if it can not be wholly loaded in the current lot).Moreover,to proceed,we can further assume that the on-time jobs inσare scheduled in the non-decreasing order of their due dates (or EDD order,breaking ties in the decreasing order of their sizes),since,otherwise,it will neither breaks out the feasibility nor increases the number of tardy jobs,when repeatedly shifting one on-time normal job with a larger due date to immediately after another one with a smaller due date.

Note that,under the above supposition,the 3ton-time normal jobs are scheduled before all the restricted jobs inσ.In fact,these 3ton-time normal jobs exactly occupy the first 3tpositions inσ,i.e.,

By (2.22) and the supposition of the jobs being scheduled in EDD order inσ,we also know

Defineκ(σ)|{j:1≤j ≤3t,The indicatorκ(σ) refers tothe coincidence numberof the first 3tjobs inσ,where by coincidence we mean that the job at thej-th position in(permutation)σexactly lies in thej-th column of the job arrayJt×3t.Obviously,κ(σ)≤3t.

Ifκ(σ)3t,then1 for each 1≤j ≤3t.Together with (2.19) and (2.20),we can conclude that the setO(σ) of the on-time normal jobs inσis a desired subset by Definition 2.1.

Thus,σ′is also a feasible schedule with no more than (in fact,exactly equal to) 3t2-3ttardy jobs.By an finite repetitions of this switching operation,we can finally obtain a desired schedule.

By Lemma 2.1 and Lemma 2.3,we finally derive the following theorem.

Theorem 2.1.The instance of 3-Partition has a solution iffthe job instance has a feasible schedule with no more than3t2-3t tardy jobs,i.e.,problem1|split,is strongly NP-hard.

§3.Results of some related scheduling problems

We will go on to discuss some scheduling problems related to problem 1|split,studied in this paper.

Theorem 3.1.Problem1|split,is unary NP-hard.

Secondly,intuitively,if we regarded the size of a job as its ‘processing time’,we can find the similarity of the model studied in this paper and the classical single-machine scheduling model.In fact,as showed soon,problems 1|split,withare respectively equivalent to the single-machine problems 1|periodic|fin which ‘periodic’ means that jobs have periodic due dates and deadlines,that is,each job’s due dates and deadlines only take values in the set{T,2T,···,nT}.Note that the criterion of the total late size is equal to the criterion ofthe total late workin the single-machine setting.

Theorem 3.2.Problems1|periodic|f with f {∑Uj,∑Yj} are unary NP-hard.