Haozhe KONG (孔浩喆), Feng WANG (王豐) and Jizhong SUN (孫繼忠)

School of Physics, Dalian University of Technology, Dalian 116024, People’s Republic of China

Abstract Adiabatic response effects on high-frequency fishbone instability driven by passing energetic ions are studied. With finite orbit width effects, the adiabatic contributionδWhf is derived analytically for purely passing energetic ions.By approximating the adiabatic contribution to the first order of the reverse aspect ratioε, we derive one of its analytic expressions, which is expected to be more accurate than that in a previous work(Graves J P 2004 Phys.Rev.Lett.92 185003). For high-frequency fishbone instability, nonadiabatic response is usually dominant over adiabatic response, but under certain circumstances the latter plays an important role,comparable to the former. With a more generalized distribution function by introducing Gaussian-type factors representing their pitch and radial dependences and using a slowing-down equilibrium distribution for the energy of energetic ions, numerical analysis indicates that the adiabatic contribution is conducive to stabilization of the mode and causes a decrease in mode frequency.In addition,we find that the adiabatic contribution has a weak stabilizing effect on the fishbone instability when the finite orbit width effect is taken into account. We further analyze the dependence of the adiabatic contribution on the characteristic parameters of the distribution function. When the neutral beam has either a larger deviation from the plasma axis or a larger radial profile, the adiabatic contribution has a more evident effect on the fishbone instability.When the neutral beam has a relatively small critical energy, the adiabatic contribution has a greater effect on the mode instability.

Keywords: fishbone, passing particle, adiabatic response, tokamak

1. Introduction

Fishbone instability driven by trapped energetic ions, first discovered in poloidal divertor experiment (PDX) plasmas[1], has drawn a great deal of attention. Later, fishbone instabilities were then observed in PBX [2], JET [3], DIII-D[4], HL-2A [5-8] and EAST [9]. These instabilities accompanied by a loss of energetic particles result in the reduction of heating efficiency. The fishbone instability observed in experiments is known to be excited by energetic particles,which can be one of trapped energetic ions,passing energetic ions or superthermal electrons, under different resonance conditions. For instance, the mode frequency of the fishbone instability was observed to be close to the toroidal precession frequency of the trapped energetic ions in the PDX while in the PBX it is around the toroidal circulation frequency of passing energetic ions [1, 2].

Based on these theories, we can understand reasonably well the physical mechanism of fishbone instability [10-14].Fishbone instabilities are internal kink modes with dominant poloidal and toroidal wave numbersm= 1 andn= 1, and can be resonantly excited by energetic ions produced by both perpendicular and tangential neutral beam injections (NBIs)[1, 2]. With the perpendicular injection, there are two theoretical explanations for the exciting conditions of fishbone instability: first, the mode frequency is comparable to the toroidal precession frequency of the trapped energetic ions[10] while the mode is considered to be an energetic particle mode (EPM); the second is that the mode frequency is close to the thermal ion diamagnetic frequency[11]while the mode is considered to be a ‘gap’ mode. With the tangential injection, theoretical prediction indicates that the fishbone instability has two branches: low- [12] and high-frequency branches [13]. The former’s mode frequency close to the thermal ion diamagnetic frequency is modeled as a ‘gap’mode, and the latter’s mode frequency determined by the toroidal circulation frequency of passing energetic ions is considered to be an EPM. The resonance condition of the high-frequency branch can be specifically expressed asω?+pωθ-ω=0, whereω?andωθare the circulation frequencies in the toroidal and poloidal directions, respectively,andp= 0 is for the EPM branch of high-frequency fishbone driven by passing energetic ions [13]. To date, the EPM branch of low-frequency fishbone forp= -1 has been well documented[14].In this work,we focus mainly on the highfrequency EPM branch withp= 0.

The ideal magnetohydrodynamic (MHD) description is usually employed to treat the thermal plasma in tokamaks.However, to handle the energetic ions the drift-kinetic description is often adopted, instead. By linearizing a driftkinetic equation, we can obtain the adiabatic response (fluid contribution)and nonadiabatic response(kinetic contribution)of energetic ions [15]. When the ion energy is high, the ion collision frequency is low (compared to the Alfvén frequency). The drift-kinetic description is obviously more appropriate for the passing energetic ions driving high-frequency fishbone instability, i.e. the nonadiabatic response(which represents a resonance interaction) plays a dominant role. However, as they slow down, the energetic ions gradually approach Maxwellian distribution,and the contribution of adiabatic response becomes more important. Thus, nonadiabatic response alone becomes inadequate for representing the energetic ions in the course of the ions slowing down, as with most scenarios in tokamaks. In other words, both the adiabatic and nonadiabatic responses are important for the energetic ions in the intermediate energy range.However,in a previous work[13,16],the contribution of adiabatic response to high-frequency fishbone instability has not been taken into account. Therefore, it is important to study the role of adiabatic response of passing energetic ions in high-frequency fishbone instability.

This paper is organized as follows. In section 2, the fishbone dispersion relation including the contribution of adiabatic response is derived. In section 3, the potential energy arising from the adiabatic contribution of energetic ions is deduced by simplifying the generic slowing-down distribution function. In section 4, the numerical results obtained using the extended dwk++[16]code in the present work are then compared with our analytical results to verify the modified code with the simplified slowing-down distribution function. Then, the effects of the distribution function parameters, such as beam ion radial profile, critical energy, pitch parameter distribution and beam ion drift orbit width on fishbone instability are studied.Finally,conclusions are given in section 5.

2. Fishbone dispersion relation including adiabatic contribution

3.Analytical description of adiabatic contribution for passing energetic ions

To obtain a clear expression of the dispersion relation, a simplified slowing-down distribution function [14] is employed:

Furthermore,following equation(19)in[16]the real part of the dispersion relation including the adiabatic contribution is given by,

4. Parameter dependence of high-frequency fishbone

4.1. Code verification

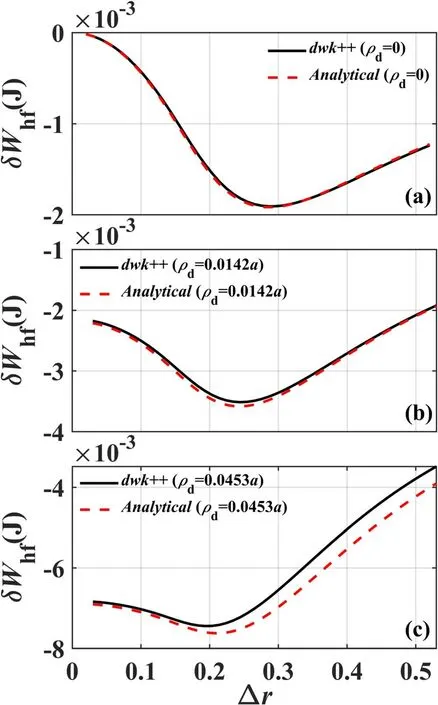
Figure 1.Adiabatic contribution of energetic ionsδWhf calculated by equation (9) (analytical results) and dwk++ (dwk++ results),respectively, versus radial profile width Δr for (a)ρd = 0,(b)ρd =0.0142a and (c)ρd =0.0453a by setting ?c =0.01? 0,Λ 0= 0.01,ΔΛ = 0.02.

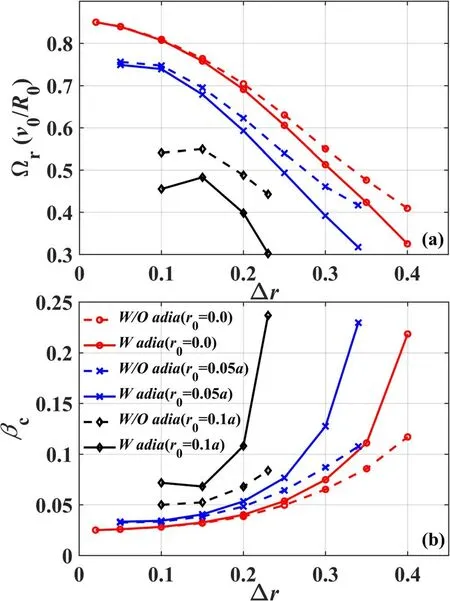
Figure 2.(a)Fishbone mode frequency Ω r ,(b)critical beam ion beta βc versus radial profile width Δr for different peaked positions,with and without adiabatic contribution (solid line and dashed line).

4.2. Radial profile effects

Figure 3.Total potential energyδW versus radial profile width Δr for r0=0.05a ,with and without adiabatic contribution (solid line and dashed line).

Figure 4.(a)Fishbone mode frequency Ω r ,(b)critical beam ion beta βc versus critical energy ?c with and without adiabatic contribution(solid line and dashed line).

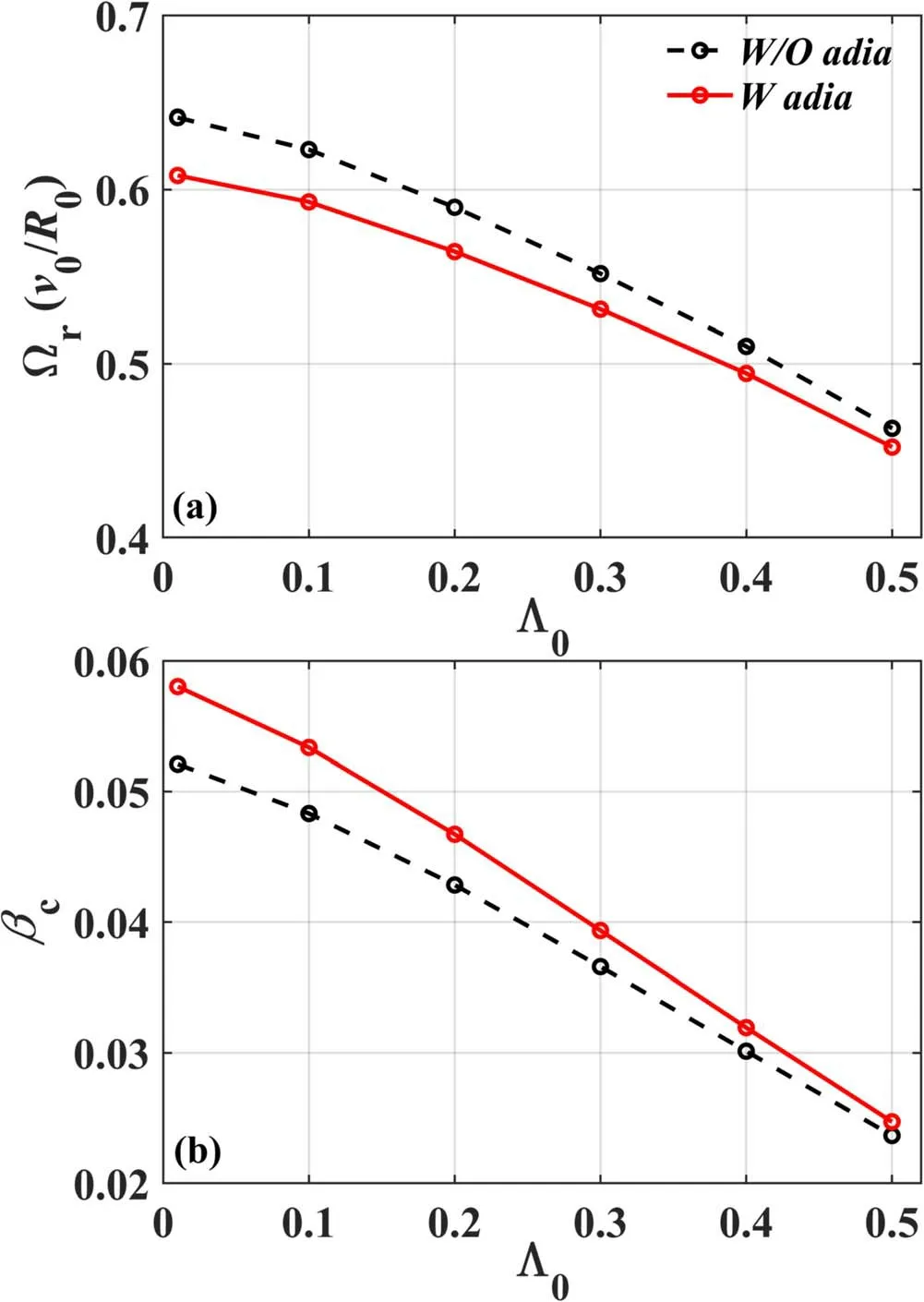
Figure 5.(a)Fishbone mode frequency Ω r ,(b)critical beam ion beta βc versus pitch parameterΛ0 with and without adiabatic contribution(solid line and dashed line).

4.3. Critical energy effects

Critical energy is a very important parameter in the slowingdown distribution function, which affects the mode stability significantly [16, 22]. Figure 4 plots the mode frequency Ωrand critical beam ion betaβcas a function of the critical energy?cwithr0=0.05a,Δr=0.2a, and the other parameters are the same as in section 4.2. It is clear from figure 4(b) that the adiabatic contribution has a significant stabilizing effect on the mode for small values of?cwhile it makes Ωrdecrease in figure 4(a). This can be understood by the fact that the change in magnitude?chas a direct effect on the equilibrium distribution function. The adiabatic contribution leads to an increase in the total potential energy, which makes the fishbone become more stable, especially for small values of?c.

4.4. Pitch parameter effects

Figure 6.Adiabatic contribution effects on (a) fishbone modefrequency Ωr and(b)critical beam ion beta βc with finite orbit width effects.

We have assumed the pitch parameter to be zero (Λ0= 0) at the equilibrium distribution peak in the previous theoretical analysis, but it is not realistic to have a pitch parameter distribution in a small range in experiments. Figure 5 plots the dependence of the fishbone mode frequency Ωrand the critical beam ion betaβcon Λ0at parameter set:?c=0.36?0.From figure 5(b), it can be observed that the adiabatic contribution has a weak stabilizing effect on the mode,i.e.the critical beam ion betaβcincreases slightly compared to that without the adiabatic contribution, and the mode frequency decreases slightly in figure 5(a).This is because the adiabatic contribution represents a non-resonant interaction, i.e. the adiabatic contribution has a weak dependence on the parameter-pitch parameter Λ0,which relates to the particle parallel velocity determining the passing particles’ transit frequency.

4.5. Finite drift orbit width effects

5. Conclusion

We have extended the model used in the dwk++ code to include the adiabatic contribution. The code is verifeid by comparison with both analytical and numerical results with and without FOW effects, respectively. The dependence of the mode frequency and stability on beam ion radial profile,critical energy, pitch parameter distribution and beam ion drift orbit width is studied with considering the adiabatic contribution.Overall, the numerical analysis indicates that the adiabatic contribution plays a positive role in stabilizing the fsihbone mode and makes the mode frequency decrease. More specifically, the adiabatic contribution has a significant effect on the mode instability for a larger value of the radial proflie widthΔror a larger deviation of the deposition location of injected neutral beam from the plasma axisr0. For a small magnitude of the critical energy?c, the adiabatic contribution effect on the mode instability is significant. Finally, the pitch parameter Λ0and the FOW have a weak effect on the adiabatic contribution.

Acknowledgments

This work is supported by National Natural Science Foundation of China (No. 11975068) and by the National Key R&D Program of China (No. 2019YFE03030004). The authors thank Prof. Limin Yu from East China University of Science and Technology for some helpful discussions.