Kamyar Hosseini, Mousa Ilie, Mohammad Mirzazadeh,Dumitru Baleanu, Choonkil Park and Soheil Salahshour

1 Department of Mathematics, Rasht Branch, Islamic Azad University, Rasht, Iran

2Department of Mathematics, Near East University TRNC, Mersin 10, Turkey

3 Department of Engineering Sciences,Faculty of Technology and Engineering,East of Guilan,University of Guilan, P.C.44891-63157 Rudsar-Vajargah, Iran

4 Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara, 06530, Turkey

5 Institute of Space Sciences, Magurele-Bucharest, R 76900, Romania

6 Research Institute for Natural Sciences, Hanyang University, Seoul 04763, Republic of Korea

7 Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

Abstract Studying the dynamics of solitons in nonlinear time-fractional partial differential equations has received substantial attention, in the last decades.The main aim of the current investigation is to consider the time-fractional Sharma–Tasso–Olver–Burgers (STOB) equation in the Caputo–Fabrizio (CF) context and obtain its valid approximations through adopting a mixed approach composed of the homotopy analysis method(HAM)and the Laplace transform.The existence and uniqueness of the solution of the time-fractional STOB equation in the CF context are investigated by demonstrating the Lipschitz condition forφ (x , t ;u)as the kernel and giving some theorems.To illustrate the CF operator effect on the dynamics of the obtained solitons, several two- and threedimensional plots are formally considered.It is shown that the mixed approach is capable of producing valid approximations to the time-fractional STOB equation in the CF context.

Keywords: time-fractional Sharma–Tasso–Olver–Burgers equation, Caputo–Fabrizio context,mixed approach, existence and uniqueness, valid approximations

1.Introduction

As we know, fractional calculus (FC) is a generalized version of classical calculus that relates to the derivative and integral of arbitrary order.FC is as old as classical calculus and has received much attention in the last few decades.Many studies with the theoretical discussion have been done within the framework of FC.So far, different fractional derivatives with singular and non-singular kernels have been proposed,some of these fractional derivatives are Riemann–Liouville derivative[1], Caputo derivative [2], Atangana–Baleanu derivative [3],and Caputo–Fabrizio (CF) derivative [4].Veeresha and Prakasha [5] studied the time-fractional Zakharov–Kuznetsov equations in the Caputo sense and derived its approximate solutions with the help of theq-homotopy analysis transform method (HAMT).Yavuz et al [6] considered the time-fractional Schr?dinger–KdV equation in the Atangana–Baleanu context and found its approximate solution through the modified Laplace decomposition method.Aydogan et al [7]explored the Rabies mathematical model in the CF sense and derived its approximate solutions through the Adomian decomposition method.For more studies, see [8–20].

The Sharma–Tasso–Olver–Burgers equation is a new nonlinear model that has been introduced by Yan and Lou in[21] and is expressed as

wherec1andc2are free constants.It should be noted that the STOB equation is a combination of the STO and Burgers equations.Yan and Lou[21]obtained soliton molecules of the STOB equation using the velocity resonant mechanism.Miao et al[22] derived lump and interaction solutions of the STOB equation by adopting different test functions.Very recently,Hosseini et al [23] found kink solitons of the STOB equation through the exponential method.The main aim of the present study is to consider the time-fractional STOB equation in the CF context and obtain its valid approximations through adopting a mixed approach[24–30]composed of the homotopy analysis method and the Laplace transform.The time-fractional STOB equation in the CF context can be written as follows

The mixed approach namely the HAMT is a powerful analytical method that has been widely used to find valid approximations for nonlinear fractional equations.Aljhani et al [27] applied the HAMT to obtain a valid approximation of a fractional HIV model in the Caputo context.Baleanu et al[28]in their paper dealt with finding a valid approximation to a fractional model of COVID-19 in the CF sense using the HAMT.The authors of[29]derived a valid approximation to a fractional model of anthrax in the CF context through the HAMT.Very newly, Hosseini et al [30]utilized the HAMT to acquire valid approximations of a timefractional nonlinear water wave equation in the Caputo sense.

With a close look at the research done in the above references, it can be concluded that the study of nonlinear fractional equations in the CF context is of particular importance in many branches of science.Therefore, here a series of required introductory definitions in the CF context that will be used in the next sections are provided.

Table 1.The absolute error of the 8th order approximation and the first exact solution.

The outline of this paper is as follows: In section 2,the existence and uniqueness of the solution of the timefractional STOB equation in the CF context are investigated by demonstrating the Lipschitz condition forφ(x,t;u) as the kernel and giving some theorems.In section 3, valid approximations of the time-fractional STOB equation in the CF context are derived through adopting the HAMT.In section 4, the effectiveness of the HATM in handling the time-fractional STOB equation in the CF context is shown.Additionally, the CF operator effect on the dynamics of the obtained solitons is investigated in detail.The outcomes of the present investigation are given in the last section.

2.The theoretical discussion on the existence and uniqueness of the solution

Supposing

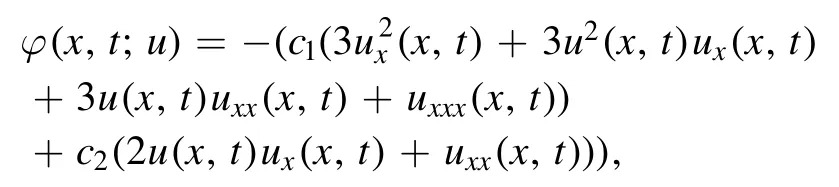
recommends that equation (1) can be rewritten as

Theorem 1.Assume thatu(x,t)andv(x,t)are the bounded functions, namely‖u‖ ≤μand‖v‖ ≤υ.Then,φ(x,t;u) is a kernel satisfying the Lipschitz condition.

Proof.

Now, assuming

yields

which is the desired result.

Theorem 2.If att=t0,we have

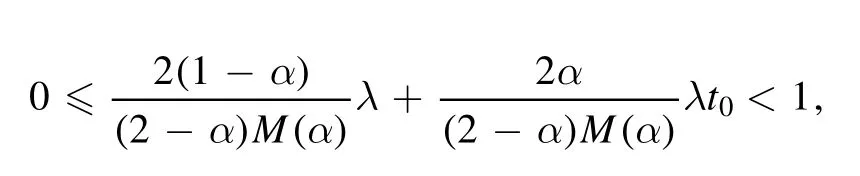
then,the solution of the time-fractional STOB equation in the CF context exists.

Proof.See [25] and its references.

Theorem 3.If att=t0,we have.

then,the solution of the time-fractional STOB equation in the CF context is unique.

Proof.See [25] and its references.

3.Analytical solutions to the time-fractional STOB equation in the CF context

The authors’ purpose in the current section is to establish analytical solutions of the time-fractional STOB equation in the CF context.In this respect, first solitons of the STOB equation are derived with the help of ansatz method.The HATM is then employed to extract approximate solutions of the time-fractional STOB equation in the CF context.The computations are handled by Maple software.

3.1.The STOB equation and its solitons

To start, we consider a test function as [32–34]

whereA0andA1are unknowns.Inserting equation(2)into the SOTB equation results in

From the above expression,the following system of nonlinear algebraic equations is obtained

The above system is solved to get the following cases:

Case 1

Therefore, the following soliton to the SOTB equation is derived

where forA0=1,c1=1,c2=1,andk=1 is changed into

with a series representation as

Case 2

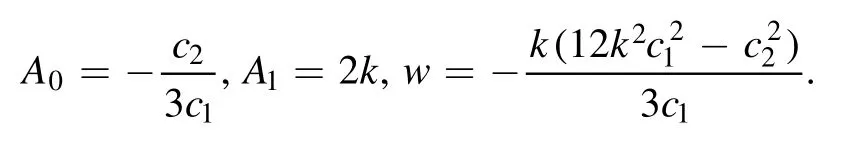
Thus,the following soliton to the SOTB equation is obtained

where forc1=1,c2=1,andk=1 can be written

with the following series representation

3.2.The time-fractional STOB equation in the CF context and its approximate solutions

By consideringc1=1andc2=1(selected by the authors)in equation (1) and adopting the Laplace transform, we find

Equation (5) recommends considering the following nonlinear operator

Based on the HAM[35],the following mth order deformation equation is formally constructed

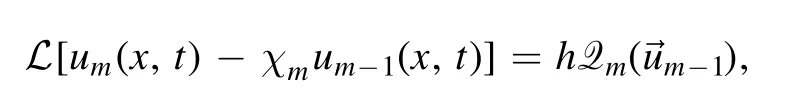
where

and

In the first step,suppose that the initial condition of the timefractional STOB equation in the CF context whenc1=1andc2=1is as follows

Considering the above initial condition and solving the resultant equations successively, yields

Consequently, the following series solution to the time-fractional STOB equation in the CF context is gained

In the special case whenα= 1 andh= -1, one can obtain

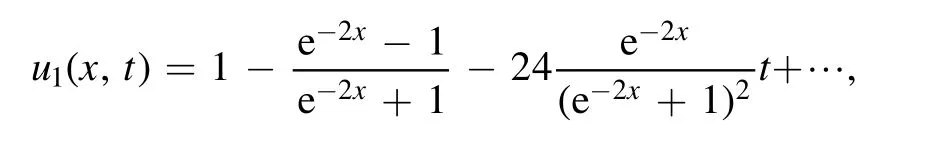
with a closed-form representation as

Now, assume that the initial condition of the time-fractional STOB equation in the CF context whenc1=1andc2=1is as follows

By considering the above initial condition and solving the resultant equations successively, one can find

Consequently, a series solution to the time-fractional STOB equation in the CF context is acquired as

In the special case whenα= 1 andh= -1, one can derive

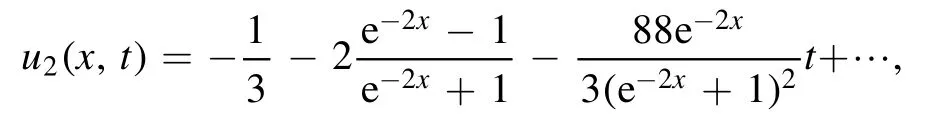
with the following closed-form representation

4.Simulations and discussion

In this section, several two- and three-dimensional plots are considered to illustrate the CF operator effect on the dynamics of the obtained solitons.Figure 1 shows the two-dimensional plot of the 4th order approximation fort= 0.001,h= -1,andα= 1,0.98, and0.96 (Selected by the authors).The CF operator effect on the dynamics of the kink soliton is formally observed from this figure.Additionally, by referring to figure 1 again, it can be observed that the results of the 4th order approximation and the exact solution (equation (3)) are in compromise.The three-dimensional plots of the 4th order approximation have been given in figure 2 forh= -1 andα= 1,0.98, and0.96.Table 1 presents the absolute error of the 4th order approximation (h= -1) and the exact solution(equation (3)) whenxi= 0.5i,i=0, 1,...,10andt=0.001.The results confirm the potential of the HATM in handling the time-fractional STOB equation in the CF context.The two-dimensional plot of the 4th order approximation fort=0.001,h= -1, andα= 1,0.98, and0.96 has been illustrated in figure 3.From this figure,the CF operator effect on the dynamics of the kink soliton is clearly seen.Furthermore, by looking at figure 3 again, it can be seen that the results of the 4th order approximation and the exact solution(equation(4))are in compromise.The three-dimensional plots corresponding to the 4th order approximation have been represented in figure 4 forh= -1 andα= 1,0.98,and0.96.Table 2 demonstrates the absolute error of the 4th order approximation(h= -1)and the exact solution(equation(4))whenxi= 0.5i,i=0, 1,...,10andt=0.001.Based on the results presented in table 2,the utility of the HATM in dealing with the time-fractional STOB equation in the CF context is confirmed.

Table 2.The absolute error of the 8th order approximation and the second exact solution.

Figure 1.The first exact solution (t = 0.001) against the 4th order approximation for t= 0.001, h = -1, and α = 1, 0.98, and 0.96.

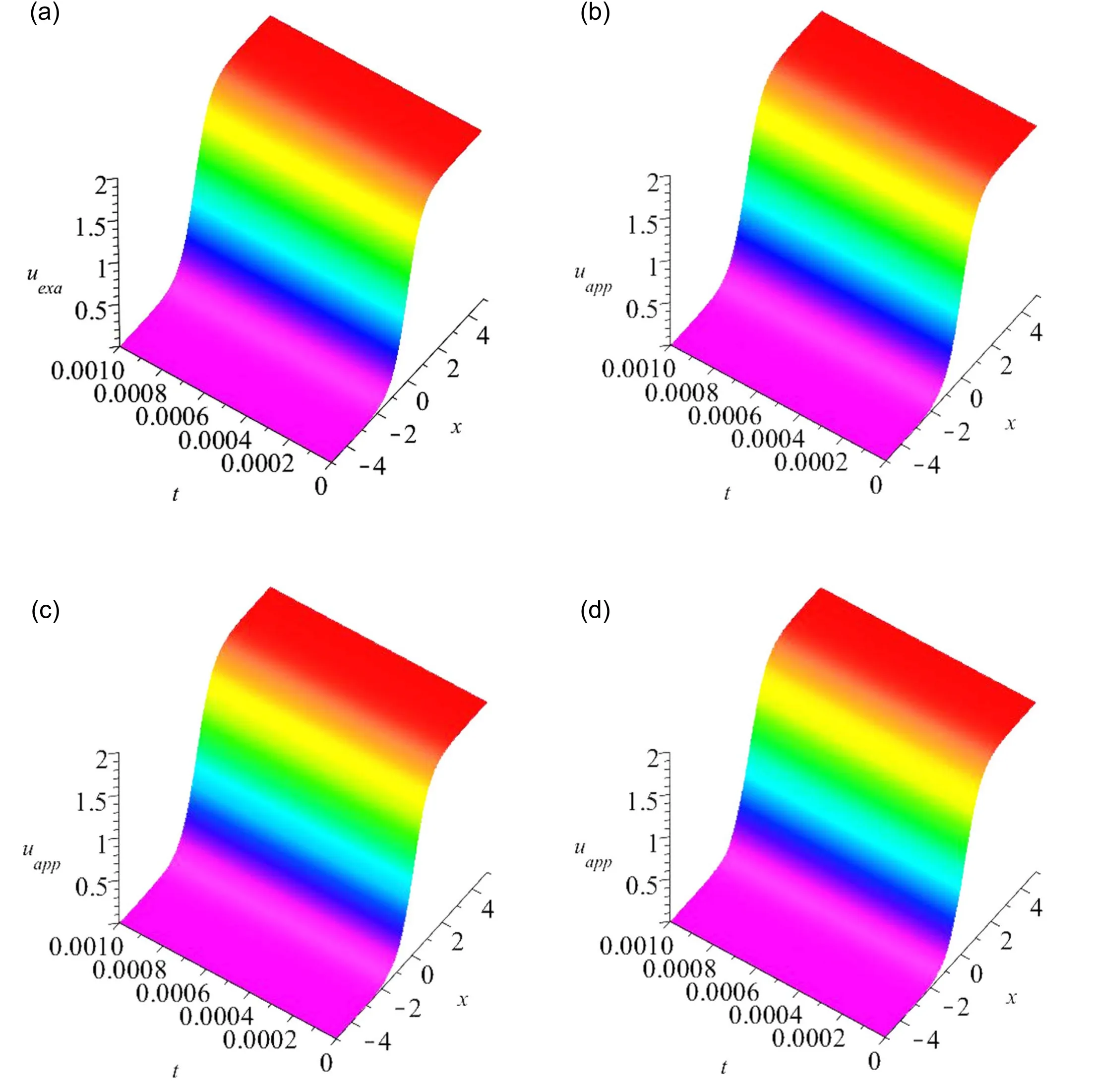
Figure 2.(a) The first exact solution against (b) the 4th order approximation for α = 1 and h= -1(c) the 4th order approximation for α = 0.98 and h= -1(d) the 4th order approximation for α = 0.96 and h= -1.

Figure 3.The second exact solution (t = 0.001) against the 4th order approximation for t= 0.001, h= -1, and α = 1, 0.96, and 0.92.

Figure 4.(a) The second exact solution against (b) the 4th order approximation for α = 1 and h= -1(c) the 4th order approximation for α = 0.96 and h= -1(d) the 4th order approximation for α = 0.92 and h= -1.

5.Conclusion

As it was stated, exploring the dynamics of solitons in nonlinear time-fractional partial differential equations has gained considerable interest,in the last decades.The key objective of the current study was to consider the time-fractional STOB equation in the CF context and acquire its valid approximations through utilizing a mixed approach composed of the HAM and the Laplace transform.The existence and uniqueness of the solution of the time-fractional STOB equation in the CF context were analyzed by proving the Lipschitz condition forφ(x,t;u) as the kernel and providing some theorems.To demonstrate the CF operator effect on the dynamics of the obtained solitons, several two- and three-dimensional plots were portrayed.It was observed that the mixed approach is capable of generating valid approximations to the timefractional STOB equation in the CF context.

Declaration of competing interest

The authors declare no conflict of interest.

Competing interests

The authors declare that they have no competing interests.

ORCID iDs