Zhenxiong Nie(聶振雄), Yun Liu(劉蕓), Juhua Chen(陳菊華), and Yongjiu Wang(王永久)

Department of Physics,Key Laboratory of Low Dimensional Quantum Structures and Quantum Control of Ministry of Education,and Synergetic Innovation Center for Quantum Effects and Applications,Hunan Normal University,Changsha 410081,China

Keywords: general uncertainty principle,quantum-corrected entropy,phase transition

1. Introduction

Hawking used semiclassical arguments to show that black holes must radiate thermally.[1]It is no doubt that this discovery is another milestone in the development of physics. The thermal nature of this radiation causes the initial pure state to be mapped to the final mixed state in a non-unitary process,which leads to the famous information loss paradox. Hawking temperature can be derived in different ways,[2]the method of quantum tunneling is the most interesting one. In addition,there have been null geodesic approach[3–8]and Hamilton–Jacobi approach,[9–11]etc. Many studies have shown that Hawking temperature has nothing to do with particular coordinate transformation or nature of the particles emitted from black holes.

When the gravitation is combined with quantum theory, the ordinary Heisenberg uncertainty principle could be extended to the generalized uncertainty principle (GUP) accompanying minimum measurable length.[12–19]The tunneling method can be used to compute the quantum-corrected Hawking temperature and the corresponding entropy,in combination with the introduction of generalized uncertainty principle. In Refs. [20–22], Wanget al.proposed the approach to understanding the quantum aspects of the black hole entropy by studying the entropy relations of multi-horizons black holes in higher dimensional (A)dS spacetime with maximal symmetries. Majumder[23]and Shenet al.[24]studied the quantum-corrected Hawking temperature and entropy of a Schwarzschild black hole under GUP. The quantum correction to the Bekenstein–Hawking entropy is logarithmic, and Romeshet al.[25]were interested only in the leading correction to the semiclassical entropy ensued in the limit of arbitrarily largeAH(AHis the eigenvalue of the area operator).In recent years,the GUP has been applied to several kinds of black holes,such as scale-dependent Hayward black hole,[26]Kehagias–Sfetsos black hole,[27]Schwarzschild–Tangherlini black hole,[28]and sub-Planckian black hole,[29]etc.

One of mysterious properties of black holes is that they have a singularity at the origin of the spacetime.[30]At the spacetime singularity,the curvatures and densities become infinite, and the physical laws are no longer predictive.[30,31]It is generally believed that the spacetime singularities reflect the incompleteness of general relativity and can be resolved with construction of quantum gravity theory. Surprisingly, Bardeen in 1968 obtained a black hole solution without a singularity in a specific form of nonlinear electrodynamics.[32]Later, more regular (non-singular)black holes were proposed, such as Hayward black hole,[33]Ay′on–Beato and Garc′?a black hole,[34]and Berej–Matyjasek–Trynieki–Wornowicz black hole,[35]etc.

The existence of dark energy and dark matter in the universe has been demonstrated in Ref. [36]. According to the standard model of cosmology,[36]our current universe contains mainly of 68.3% dark energy, 26.8% dark matter and 4.9% baryon matter. Therefore, it is important to study the black hole surrounded by dark matter or dark energy.In recent years,the black hole surrounded by quintessence dark energy has attracted great interest. For example, Kiselev[37]studied the Schwarzschild black hole surrounded by the quintessential energy. Then, Toshmatov and Stuchl′?k[38]extended it to the Kerr-like black hole. In Ref.[39],Abdujabbarovet al.studied the Hayward black hole surrounded by quintessence. In addition, Kiselev proposed perfect fluid dark matter(PFDM)as a dark matter candidate.[37,40]In this work, we devote to effect of addition of GUP on thermodynamics of the Bardeen black hole surrounded by PFDM.

This paper is organized as follows. In Section 2, we briefly review the basic equations of the black hole thermodynamics. In Section 3,we study the thermodynamic properties of Bardeen black hole in PFDM,we calculate the mass of the black hole,Hawking temperature,surface gravity,the heat capacity at event horizon,and rate of emission of energy through event horizon,etc.We numerically analyze their properties for the Bardeen black hole in PFDM.In Section 4, we reanalyze the thermodynamics of the Bardeen black hole in PFDM under general uncertainty principle. Finally,we discuss and summarize our results in Section 5. Throughout this paper, we setG=ˉh=c=κB=1.

2. Basic equations

2.1. Derivation of black hole temperature

The surface gravityκof a black hole can also be defined as the magnitude of the gradient of the norm of horizon generating Killing fieldχa=ζa+ΩΨa, evaluated at the horizon.Supposing that the event horizon of a black hole is a Killing horizon,we have

From the above three different methods of derivation of temperature,it can be seen that the expressions of temperature are the same.

2.2. Heat capacity

The heat capacity, i.e., the specific heat at event horizon of a black hole is given as

It is well known that the heat capacity can decide the stability of the thermodynamical system:If the specific heat is positive,the black hole will be thermodynamically stable.If the specific heat is negative,the black hole will be thermodynamically unstable. There is also a critical case in which the specific heat blows up, and it signifies a second-order phase transition for such black hole.

2.3. Generalized uncertainty principle

3. Thermodynamic properties of the Bardeen black hole in PFDM

Let us consider the coupling between Einstein gravity and a nonlinear electromagnetic field,it is described by the following equations:

In the case of vanishingg, it reduces to the Schwarzschild black hole surrounded by PFDM.[40,50]In the case of vanishingk, it reduces to the Bardeen black hole.[52]In the case of vanishinggandk,it reduces to the Schwarzschild black hole.

The Bardeen black hole(k=0)is regular everywhere as mentioned in the introduction. To test whether this property is altered by the presence of PFDM,we calculate the following curvature scalars:

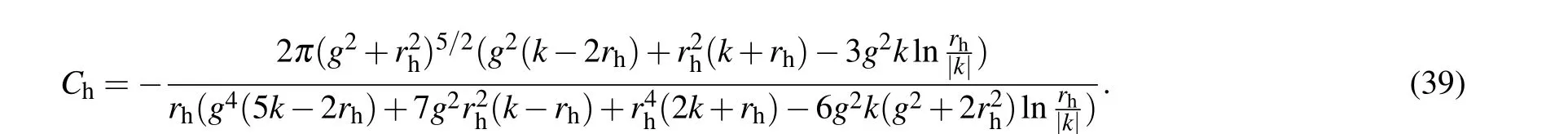
The specific heatChwith respect to event horizonrhfor different dark matter parameterskwith three different values of magnetic chargegis depicted in Fig. 2. As we can see, the specific heatChis positive and increases with event horizonrhfirstly, then specific heatChdiverges and becomes negative. Physically, the black hole is thermodynamically stable and small firstly, then it goes through a second-order phase transition,becomes thermodynamically unstable and large. At the same time, we find that the second-order phase transition occurs at a larger radius of event horizon with the increase of magnetic chargeg. However, the increase of dark matter parameterkmakes the second-order phase transition shift to a smaller radius of event horizon.

Fig.1. The variation of Hawking temperature Th with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g.

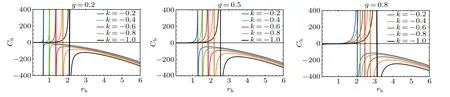
Fig.2. The variation of specific heat Ch with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g.

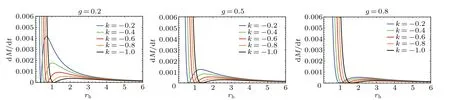
Fig.3. The variation of rate of emission dM/dt with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g.

The rate of emission dM/dtwith respect to event horizonrhfor different dark matter parameterskwith three different values of magnetic chargegis shown in Fig.3. From the curves,we can see that the rate of emission dM/dtdecreases rapidly at first,then increases and reaches a maximum,finally decreases slowly with event horizonrh. Clearly,one can find that the maximum occurs at a larger radius of event horizon with magnetic chargeg. However, the maximum occurs at a smaller radius of event horizon with dark matter parameterk.

4. Thermodynamics of the Bardeen black hole in PFDM under GUP

Supposing that the event uncertainty near the event horizon is given by Δx ?2rh,[55]the quantum-corrected temperature of the black hole is

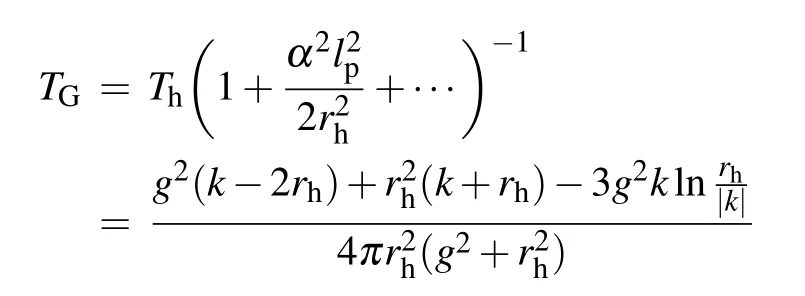
We have simulated the GUP corrected Hawking temperatureTGwith respect to event horizonrhfor different dark matter parameterskwith three different values of magnetic chargegby fixing the generalized uncertainty principle parameterα=0.1, 1 and 10 in Fig. 4. (I) Whenα=0.1, we observe thatTGincreases first and after reaching its maximum at a certainrh=rh-crit1(g,k,α), then decreases with event horizonrh. Ifg1＞g2,we can seerh-crit1(g1,k,α)＞rh-crit1(g2,k,α).Ifk1＞k2, we can findrh-crit1(g,k1,α)＜rh-crit1(g,k2,α),which means that the maximum value will occur at a larger radius of event horizon with the increase of magnetic chargeg, but at a smaller radius of event horizon with the increase of dark matter parameterk. (II)Whenα=1,the steepness of increase/decrease reduces and the maximum of Hawking temperatureTGoccurs at a larger radius of event horizon compared with the case I. (III) Whenα=10, the Hawking temperatureTGincreases firstly,the maximum occurs very late. Generally,ifα1＞α2,rh-crit1(g,k,α1)＞rh-crit1(g,k,α2).

Fig.4. The variation of GUP corrected Hawking temperature TG with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g and generalized uncertainty principle parameter α.

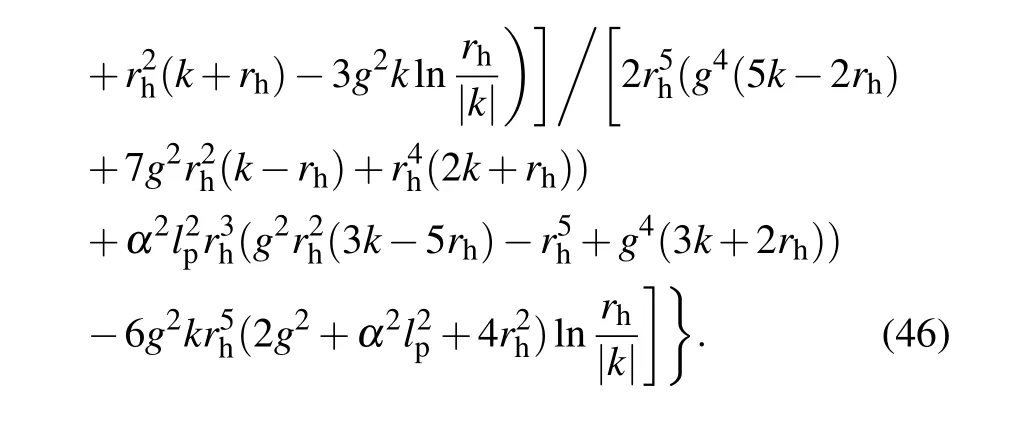
Figure 5 shows the variation of GUP corrected specific heatCGwith event horizonrhfor different dark matter parameterskwith three different values of magnetic chargeg. (I)Forα=0.1,we observe thatCGis positive firstly,then it blows up and becomes negative. Physically,the black hole is thermodynamically stable and small firstly, then it goes through a secondorder phase transition, becomes thermodynamically unstable and large.If the phase transition occurs atrh=rh-crit2(g,k,α),then we seerh-crit2(g1,k,α)＞rh-crit2(g2,k,α)forg1＞g2andrh-crit2(g,k1,α)＜rh-crit2(g,k2,α) fork1＞k2, which means that if magnetic chargegincreases, the second-order phase transition will occur at a larger value ofrh, however if dark matter parameterkincreases, the second-order phase transition will occur at a smaller value ofrh. (II)Whenα=1, the second-order phase transition occurs more later than case I.(III)Whenα=10,a stable black hole is presented first,and the phase transition takes place very late. Generally, ifα1＞α2,rh-crit2(g,k,α1)＞rh-crit2(g,k,α2).

Fig.5. The variation of GUP corrected specific heat CG with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g and generalized uncertainty principle parameter α.

Fig.6. The variation of GUP corrected Helmholtz free energy FG with respect to event horizon rh for different dark matter parameters k with different values of magnetic charge g and generalized uncertainty principle parameter α.

Obviously, forα →0, we can obtain the heat capacity shown in Eq.(39),i.e.,

Figure 6 shows the variation of quantum-corrected Helmholtz free energyFGwith event horizonrhfor different dark matter parameterskwith three different values of magnetic chargeg. (I) Whenα=0.1,FGincreases at a high rate with event horizonrh,reaches a maximum,then decreases,and lastlyFGcomes back to increase at a slightly lower rate with event horizonrh.Clearly,we can see that the maximum occurs at a larger value ofrhwith the increase of magnetic chargeg. (II) Forα=1, the rate of this increase and decrease slows down for low value of event horizonrhand the maximum occurs more later compared to the case I.(III)Whenα=10,the maximum occurs more later compared with the case II.

The quantum-corrected rate of emission is

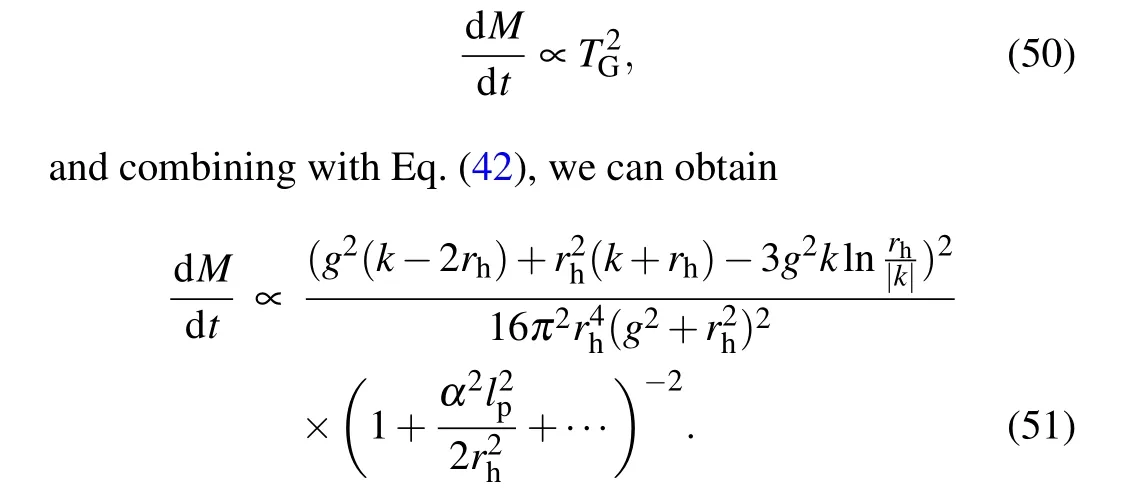
5. Discussion and conclusion

In summary, we have studied the Hawking temperature,surface gravity,and the entropy,etc.,of the Bardeen black hole surrounded by perfect fluid dark matter.Moreover,we have reexamined these thermodynamic properties under general uncertainty principle. We have also found that the quantumcorrected entropy term contains the logarithmic term of event horizonrh, which was proposed in Ref. [25]. We have observed that the Hawking temperature of the Bardeen black hole in PFDM increases and reaches a local maximum, then decreases. The specific heat diverges at the temperature maximum point at which a second-order phase transition occurs.Considering general uncertainty principle, the maximum occurs at a larger radius of event horizon when the values of magnetic chargegand generalized uncertainty principle parameterαare very high and the value of dark matter parameterskis low. From the specific heat curves, the magnetic chargegmakes the second-order phase transition take place at a larger radius of event horizon,but the dark matter parameterkmakes the second-order phase transition take place at a smaller radius of event horizon. Furthermore, GUP’s effect makes the second-order phase transition occur at a larger radius of event horizon.

Acknowledgement

This work was supported by the National Natural Science Foundation of China(Grant No.U1731107).