Hong-Yu Guo(郭宏宇) Tao Cheng(程濤) Jing Li(李景) and Ying-Jun Li(李英駿)

1State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology,Beijing 100083,China

2School of Science,China University of Mining and Technology,Beijing 100083,China

3Beijing Aeronautical Technology Research Center,Beijing 100076,China

Keywords: Rayleigh-Taylor instability,interface coupling effect,inertial confinement fusion

1. Introduction

When the heavier fluid is supported or accelerated by the lighter one,the perturbed fluid interface between two fluids is subject to Rayleigh-Taylor instability(RTI).[1,2]RTI is widely exist in laboratory experiments, such as magneto-inertial fusion (MIF)[3]and inertial confinement fusion (ICF).[4,5]The RTI is considered to be a critical mechanism for the whole perturbation growth in ICF implosions.[4]The typical ICF central ignition capsule contains two fluid layers, the imploded fuel shell is distributed on the inside and the outside is surrounded by an ablation layer. Therefore, there are at least three interfaces for the implosion capsule,namely,the ablation interface,the fuel-ablator interface, and the hot-spot interface. During the acceleration phase of the implosion, the high density fuel shell is accelerated by the ablative plasma and the ablation interface is subject to RTI. The hot-spot interface is also suffer to RTI in the deceleration stage where the heavy fuel shell is decelerated by the internal light hot-spot. The RTI growth can cause the ablator material to mix into the hot-spot, limit the implosion compression of the fuel, and even destroy the integrity of the implosion shell. More seriously,the RTI would hinder the formation of hot-spots,resulting in the degradation of ICF implosions. Because of its importance and significance to the basic research and engineering application for ICF implosion, it is still a key issue to investigate the RTI growth in the ICF implosions.

2. Theoretical model

In the present work,a finite-thickness shell with fluid densityρand thicknessdis immersed in a gravitational field-g?ey, as displayed in Fig. 1. Both sides of the fluid shell are vacuum. The finite-thickness fluid is considered to be incompressible, irrotational, inviscid, and immiscible. A twodimensional Cartesian coordinate is used, wherexandyare along and normal to the upper interface of the fluid shell, respectively. The unperturbed upper and lower interfaces are located aty=0 and-d, respectively. In the following discussion, the physical quantities on the upper interface are indicated by superscript “u” and that on the lower interface by“l(fā)”,unless otherwise indicated.

Fig. 1. Schematic drawing of finite-thickness fluid shell considered in this paper.

The velocity potential related to the incompressible fluid that can be written as

whereA0andB0are initial perturbation amplitudes at the upper and lower interfaces,θis the initial phase difference of the perturbations at the two interfaces. Then,using the initial conditions Eqs.(11)and(12),the linear solutions for the RTI growth of the perturbations are derived as

If the initial phase differenceθ=0, the classical thirdorder WN results for finite-thickness RTI are recovered.[23,24]As can be seen, the perturbation growth and interface deformation of finite-thickness are dependent on the shell thickness and the initial phase differenceθ. That means phase differenceθplays an important role in WN evolution of finite RTI which will be discussed in the following.

3. Results and discussion

In this section,the WN evolutions of RTI on the two interfaces of finite-thickness shell with arbitrary phase differenceθare studied. The dependence of interface deformation and bubble-spike growth on the shell thickness and phase difference are illustrated in some detail.

In Fig. 2, temporal evolutions of perturbed upper and lower interfaces are displayed atγt=5.0 for initial phase differenceθ=0,π/4,3π/5,andπ. The initial perturbation amplitudes areA0=B0=0.001λ, whereλ=2π/kis the perturbation wavelength withk=1. Theθ=0 (in phase) case for finite-thickness RTI[24]is shown for comparison. As can be seen,initial cosinusoidal perturbations develop into bubblespike structure in the WN stage for a thin shell.Because of the interface coupling effect, the upper interface (initially stable)also becomes unstable. The larger phase differenceθleads to more obviously irregular deformation of the shell. Although the initial phases of perturbations on the upper and lower interfaces are different,the phases of the perturbation growth at the two interfaces become the same with time proceeding. That means only a bubble and a spike exist in one period along the horizontal direction.However,we can also found that the positions of the bubble and the spike are related to the initial phase differenceθ. When the perturbations on two interfaces are in phase(θ=0),the spike position isxspike=0.5λ. When phase difference isθ=π/4,the position of spike isxspike～0.618λ.In ICF implosions, the perturbation source at the interfaces of the shell can be either initial perturbations or feedthrough among the shell during the implosion. As the perturbations on the two interfaces are random,perturbations on the two interfaces with phase difference will be a common phenomenon in the process of ICF implosion that should be considered carefully.

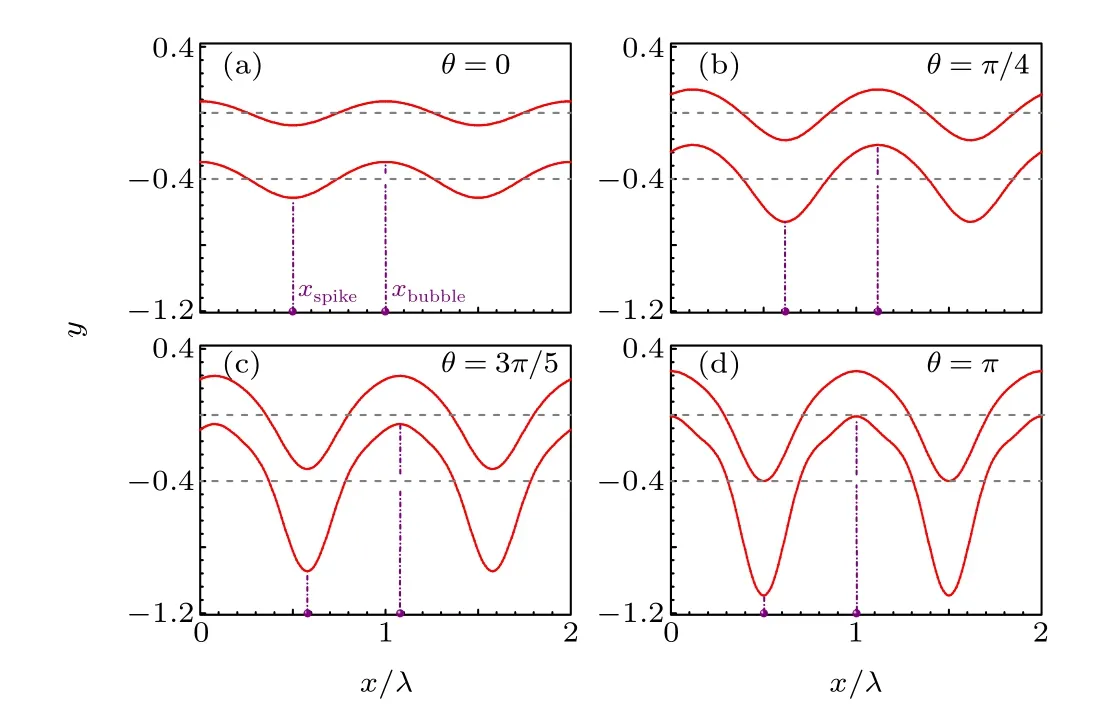
Fig.2. Temporal evolutions of interface positions of upper and lower interfaces at γt =5.0 for phase difference θ =0 (a), π/4 (b), 3π/5 (c), and π(d). The dashed lines represent the unperturbed shell with shell thickness kd=0.4. The initial perturbations are A0=B0=0.001λ.

The distance between the adjacent bubble and the spike isλ/2, which implies that the main structure of the interface caused by RTI for differentθremains unchanged (retaining the characteristics of single-mode RTI perturbation). However,the positions of the bubble and the spike are related toθ.The position of the spike corresponds to the position where the perturbation amplitude is maximum, which can be obtained using the formulas(16),(18),and(19),as

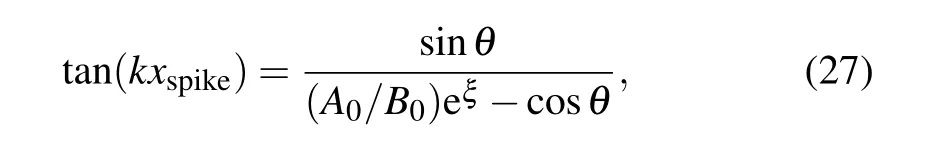
the explicit dependence of thicknessξand phase differenceθare shown. The dependences of the spike positionxspikeonkdandθare displayed in Fig. 3. As the phase differenceθincreases toπ, the normalized spike positionxspike/λincreases gradually to the maximum and then decreases to 0.5.The larger shell thicknesskdresults in the smaller the maximum position of the spike under the same conditions. Whenkdapproaches 4.0,the position of the spike is not affected by the phase difference,as the upper and lower interfaces are decoupled for a thick shell. We can also obtain from Eq. (27)that the position of the spike is determined by the coupling between two interfaces in the linear stage. The specific shape and growth of bubble-spike asymmetry are also affected by the phase difference which will be discussed later. Thus,it is found that phase difference of perturbations on two interfaces play an important role in the WN evolution of the shell, especially forkd ＜1. In typical ICF implosions, a thin shell is imploded inward,phase difference will cause the spike of the fluid to move in the vertical direction of the implosion acceleration. Then,the integrity of the shell will be destroyed,which will accelerate the mixing of ablated materials and DT fuel,thereby affect implosion compression and reduce energy gain.

Fig. 3. The position of the spike tip xspike/λ versus the initial phase difference θ for kd = 0.2, 0.4, 0.8, and 4.0. The initial perturbations are A0=B0=0.001λ.

The distortion of the shell is exhibited in Fig.4 by studying the evolution of shell thicknessdspikeat the spike tip anddbubbleat the bubble vertex. The evolution of normalizeddspike/danddbubble/dwith differentθare displayed in this figure. The shell thicknessdspikeincreases with time proceeding butdbubbledecreases with timeγt. That means the growth of finite-thickness RTI exacerbates the deformation of the shell.As can be seen,thedspikeincreases withθbutdbubbledecreases withθ. Thus,the in phase case(θ=0)for the growth of perturbation at the two interfaces of the shell will underestimate the perturbation growth. The phase difference of perturbation should be considered when predicting shell deformation in ICF implosions.

Fig.4.Temporal evolutions of shell thickness at the spike tip(a)and the bubble vertex(b)for initial shell thickness kd=0.5.The initial phase differences are θ =π/4,π/2,and π,respectively.

In Fig. 5, the evolution of dimensionless velocityvspike(k/g)1/2of spike andvbubble(k/g)1/2of bubble for different initial phase differenceθare analyzed. The velocity of spike tipvspikeincreases with time,the larger phase differenceθleads to larger spike velocity. The velocity of bubble vertexvbubblegrows gradually with time, the bubble velocity is sightly affected by phase differenceθ. The velocity of spike is sensitivity to the phase difference until late nonlinear stage.Therefore,it is necessary to consider the influence of the initial phase difference on the perturbation growth in ICF implosion.

Temporal evolutions of fundamental modeη(1)cos/λfor cosine mode perturbation are displayed in Fig.6(a)and the corresponding second harmonic generation-η(2)cos/λis shown in Fig. 6(b). For different phase differenceθ, theη(1)cosgrows gradually to a maximum with timeγt, and then decreases quickly.Since the decreasing amplitude in the WN stage is unrealistic,the scope of application of the third-order WN theory is before the fundamental mode exceeding the maximum amplitude.The large phase differenceθresults in larger perturbation growth of the fundamental mode. The negative amplitude-η(2)cosmeans the phase of the second harmonic changes byπin comparison to the fundamental mode. When the second harmonic is generated,the bubble-spike structure on the interface is formed. As can be seen, the largerθleads to larger perturbation amplitude-η(2)cos, the more round bubble tip and more narrow spike tip can be obtained.Thus,we can conclude that the perturbation growth and bubble-spike deformation are affected byθ, which is consistent with the phenomenon observed in Fig.2.

Fig.5. Temporal evolutions of the velocity of spike tip vspike(k/g)1/2 (a)and bubble vertex vbubble(k/g)1/2(b)at the lower interface of the shell.The initial phase differences are θ =π/4,π/2,and π,respectively.

Fig.6. Temporal evolution of normalized amplitudes of the perturbation fundamental mode η(1)cos/λ (a)and the second harmonic-η(2)cos/λ (b). The initial phase differences are θ =0(CRTI),π/4,π/2,and 3π/5,respectively.

Fig. 7. Temporal evolutions of normalized amplitudes of the perturbation fundamental mode ηs(i1n)/λ (a) and the second harmonic -ηs(i2n)/λ (b). The initial phase differences are θ =π/4,π/2,and 3π/5,respectively.

4. Conclusion

The WN model for RTI growth of finite-thickness incompressible shell is investigated analytically, considering that there is an arbitrary phase difference for the perturbations at the upper and lower interfaces. The third-order solutions are obtained to describe the perturbation growth and the shell deformation. When the phase differenceθ=0, the WN results for RTI growth of a finite-thickness slab are recovered.[24]The phase difference plays an important role in perturbation growth and the deformation of imploded shell for ICF implosions. The largerθleads to more obvious bubble-spike structures at the shell interfaces. That means largerθresults in more round bubble shape and more narrow spike tip. Meanwhile,the positions of bubble and spike are dependent on shell thicknessdand phase differenceθ. For a thin shell implosion, the initial cosine-mode perturbations on two interfaces are coupled,and the sine-mode perturbation will be generated with the time proceeding which affects the position of bubblespike structure. The analytical model is expected to improve the understanding of the interface coupling and initial perturbation phase effect on the RTI growth of a finite-thickness shell in ICF implosion. It is notable that the potential influences of compressibility are not included in our model. They are quite important for ICF. Considerations of compressibility effects are beyond the scope of this work, which will be pursued in the future.

Acknowledgments

Project supported by the Fundamental Research Funds for the Central Universities,China(Grant No.2021YQLX05),the National Natural Science Foundation of China (Grant No. 11974419), and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant Nos.XDA 25051000).