汪誠博 ,石亞偉 ,冉 亮 ,鄭祖卿 ,李華青

(1.西南大學(xué)西塔學(xué)院,重慶 400715;2.西南大學(xué)電子信息工程學(xué)院非線性電路與智能信息處理重慶市重點(diǎn)實(shí)驗(yàn)室,重慶 400715)

1 Introduction

With the development of digital smart grid sensing,the efficiency,the reliability and the security of power systems have been substantially improved[1].As important components of dynamic energy resources(DERs),distributed generation(DG)and energy storage(ES)play a crucial role in fast responding.Thus,DERs can work as a valuable system by coordinating with system requirements and control processes[1].The traditional centralized control mechanisms for DERs require a center receiving information from the entire network and sending control signals back to the system[2-3].However,there exit some limitations,such as the heavy communication burden and single-point-of-failure,under the centralized methods.In contrast,distributed methods possess stronger robustness and extensibility,which are widely applied in smart grid,resource allocation,Nash equilibrium,machine learning,and other scenarios[4-8].

In distributed algorithms,each agent (distributed generation or storage device)receives information from neighbors and makes its own decision.Some existing studies only consider a single type of DERs,such as DGs in[9-10] and ESs in[11-12].To coordinate multiple types of DERs,the authors in[13]proposed a distributed energy management algorithm based on consensus+innovations method.In[14],the Laplacian gradient dynamics and dynamic average consensus was employed to design a distributed algorithm for coordinate DGs and ESs.The authors in[15]improved the distributed DERs coordination algorithms by considering the charging and discharging efficiency.In recent years,environmental issues have attracted attention,and it would be more practical to consider environmental factors in the DERs model.Inspired by this fact,we introduce environmental cost functions in the DERs coordination problem,which further refines the DERs model.

This paper focuses on a DERs coordination problem with DGs and ESs,where the involved constraints include local output capacity limitations,coupled supply-demand equality,ramping up/down constraints,storage capacity limitations for energy storages devices,and the limits of state-of-charge of the storages.Unlike recent works[1,9-17]that only consider the cost of generations,we additionally introduce the environmental cost.Considering that the complexity of the DERs model may make itself difficult to be solved,we first simplify it into a generalized minimization problem and further construct its dual setup by using the Lagrangian function.Inspired by the distributed primal-dual method[18],we put forward a novel distributed splitting algorithm to deal with DERs problem,essentially distinguishing from the consensus methods[16-17,19].The proposed algorithm only relies on local step-sizes rather than coordinated ones[1],guaranteeing the privacy of agents.Meanwhile,the involved relaxed constant enhances the flexibility of algorithm implementability through setting different values.To our knowledge,there only are a few works for solving the DERs coordination.Finally,we verify the correctness and effectiveness of the proposed algorithm by using the IEEE 39-bus system.

The remainder of this paper is arranged as follows:Section 2 formulates the DERs coordination problem,and Section 3 describes its dual setup.Then,the development of distributed algorithm is presented in Section 4.In Section 5,simulation results are reported.A conclusion and future work are given in Section 6.

2 Problem formulation

In this paper,an optimal coordination of DERs containingsDGs andvESs is considered,the objective of which aims to collaboratively minimize the total cost,while all agents (including generations and storages) has to satisfy a given supply-demand through communication exchange during certain time slotT{1,...,n}.Next,more details on the considered problem are described below.

The total cost over the time slotTtakes form of

where(.)and(.)are respectively generation cost and environmental cost functions of agenti,whilepi,tis its output power at the instant.In this paper,we assume that both of the cost functions are strongly convex,which is common in recent literature[21,24].At time period,all agents need to meet the supplydemand constraint

with the time-varying demandDt.For each generation,the outputpi,tis restricted by the capacity limitation

and the ramping up/down constraint

For each storage,the outputpi,tis given by

Furthermore,each storage dynamically stores the energyEi,tat

As stated above,we can formulate the DERs coordination problem as the following constrained optimization one:

which subjects to(2)-(8).To address this problem(9),we define the local objective function

withpi[pi,1pi,2...pi,n]TRn.LetSandMbe the sets of DGs and ESs,respecti-vely.Then,the local constraint corresponding topiis given by

wherems+vis the total number of agents,AiRn×nis a linear transformer andbi[D1/m ...Dn/m]TRnis the virtue local demand,some discussion of which can refer to[19].

As a result,the dynamic optimal coordination of DERs(9)can be addressed through solving the general model(11).

3 Dual problem

This section formally constructs the dual setup of(11).First of all,let’s consider the Lagrangian function

Next,construct the dual function

from of which the unique optimal solution of (11) can be given by

Consequently,we can solve the DERs coordination problem(9),by addressing the following minimization dual problem:

Note that the Lagrange multiplier ?λis known by all agents,which prevent us from solving the DERs coordination problem in the distributed manner.To this end,each agent has to maintain its own local variablesλito estimate ?λ,and further communicate with its neighboring agents to achieve the consensus state.

In what follows,we considermagents communicating over an undirected graphG,consisting of the vertex setV{1,...,m}and edge setEV ×V.Then,the obtained dual problem(17)can be equivalently rewritten as the following constrained problem:

whereλthe linear operatorUijIifi ＜jand-Iifi ＞j.The coupled edge constraint reveals that neighboring agents,linked by(i,j),will locally shareUijλiandUjiλjwith each other.Next,we define the following operator:

where the edge-based linear operatorN(i,j)is expressed by

Define the set

The coupled edge constraint in(18)can be constrained by the following indictor function

Thus,we obtain the unconstrained formulation of(18)

4 Distributed algorithm for DERC

Inspired by the forward-backward splitting[18],this section develops a new distributed algorithm to deal with the globally optimal solution of optimization problem(23).According to[23,Proposition 19.18],one can derive the Lagrangian function of(23)as follows:

Using Moreau decomposition[41],one can decompose the first line of(24)into

Combing the projection ofZ(i,j)

For ease of computation,let

then chooses the parametersτi,κ(i,j)andα.Fork ＞0,each agentcarries out the local updates

Fig.1 The flowchart of operations of an agent

Remark 2Although the proposed algorithm (see(28)-(29)) is based on the forward-backward splitting[18],its update formulations are totally different from that of the distributed forward-backward algorithm.In particular,the distributed algorithm(24)cannot be accessible to deal with problem (23),since the complex composite function ?ficontains a conjugate function.Fortunately,using the strong convexity assumption on cost functionCiand the equality(27),we can smoothly and explicitly evaluate the derivatives of ?fiand obtain the new algorithm (28)-(29),which is the essential difference compared with(24).Finally,as a convergence rate is not established in[18],we explore the possible superiority of our proposed algorithm that adopts the constant relaxed factor,through the simulations.The work in terms of this issue are still studied in the future.

Theorem 1[18,Theorem 1] Suppose that the local step-sizesσi ＞0,κ(i,j)＞0,and 0＜α ＜1.Meanwhile,τineeds to meet

Remark 3It is worth mentioning that the algorithm(28)-(29) inherits the convergence of the distributed one[18],the key analysis line of which is to establish the Krasnosel’skii-Mann iteration[18,Lemma 1].Here we report the convergence results by Theorem 1 and omit the detailed proof.Other comments on the convergence results can refer to[18].

5 Illustrative example

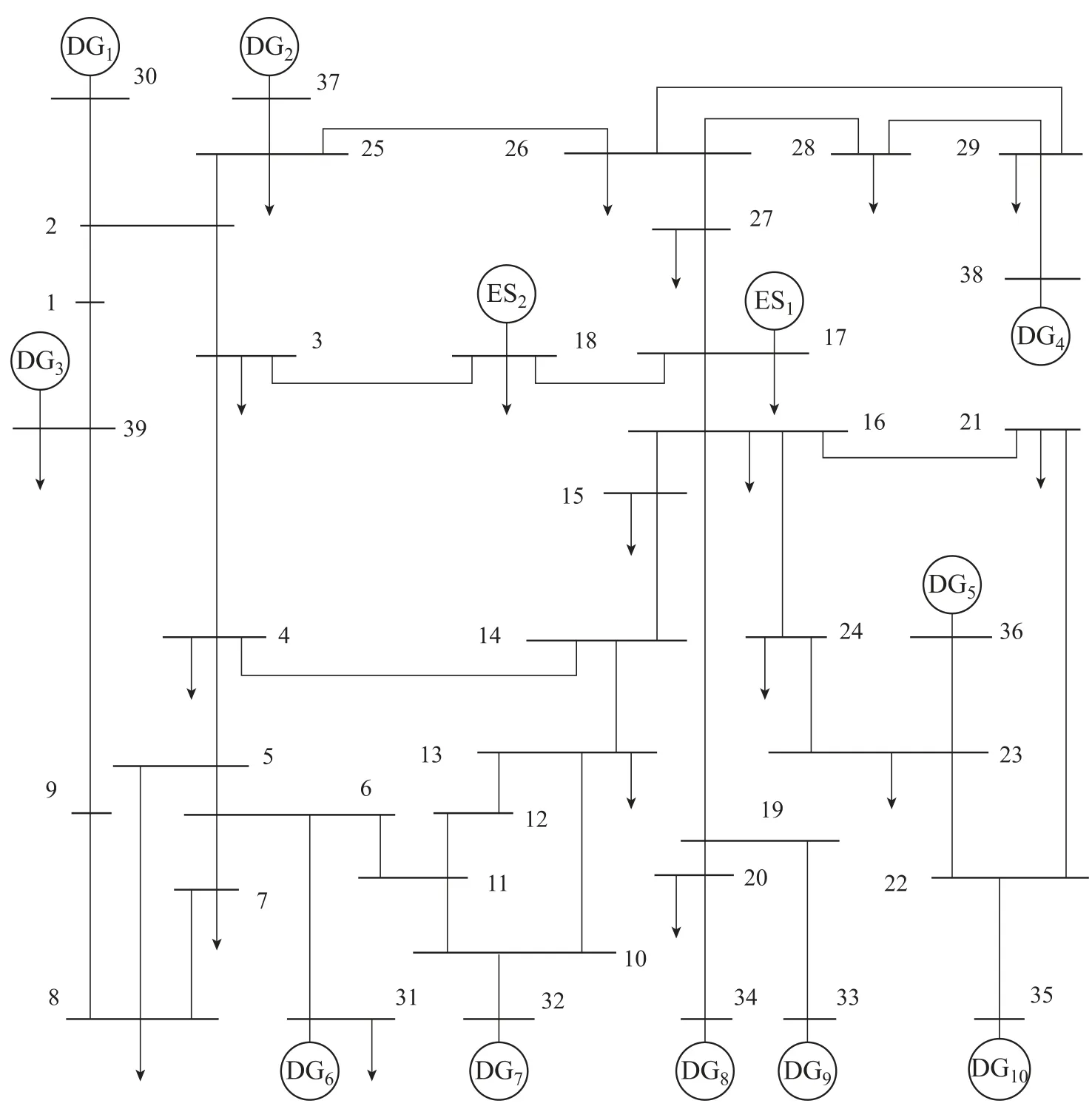
Fig.2 IEEE 39-bus system.

The results are shown in Figs.3-9.Fig.3 presents the role of ESs in cutting the peak and filling the valley.Specifically,the ESs discharge at peak periods(hours 12-16)and charge at the valley periods(hours 2-4).Fig.4 plots the optimal power generated by the DGs and ESs for 24 hours,and Fig.5 indicates that the total generation meets the total demand at hour 18 after 1500 iterations for Alg.1.The state of charge(SOC) and power output for the ESs are plotted in Figs.6 and 7,where SOC is represented by a percentage of the rated capacity of ES,while discharging power by a positive value and charging power of ES by a negative one.In addition,the total charging power is not less than the total discharging one due to the charging and discharging efficiency.

Fig.3 Cut the peak and fill the valley

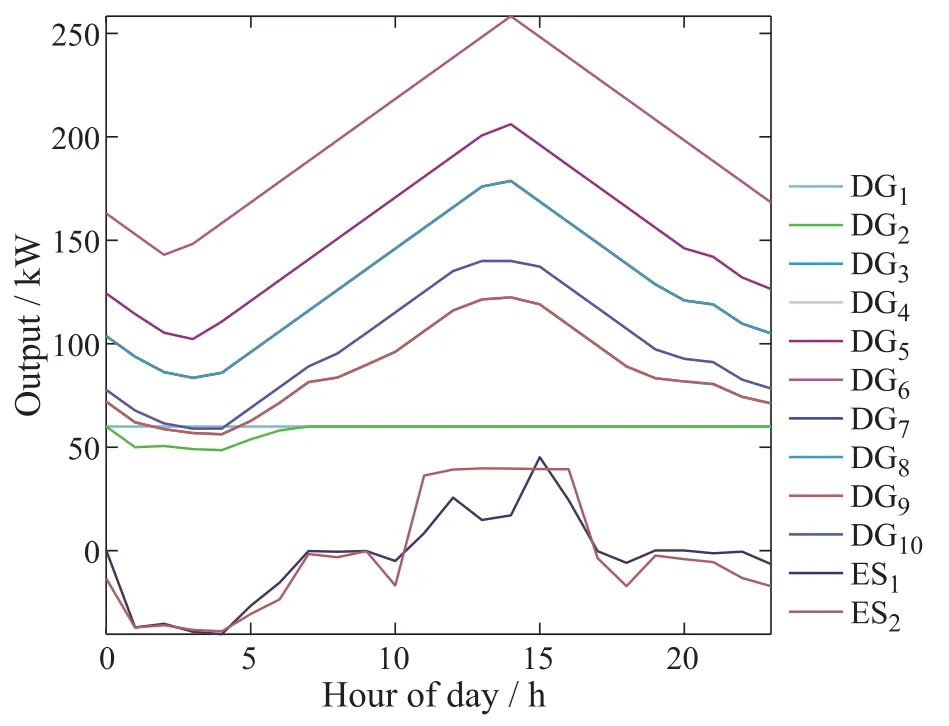
Fig.4 Optimal power output for DGs and ESs over a day

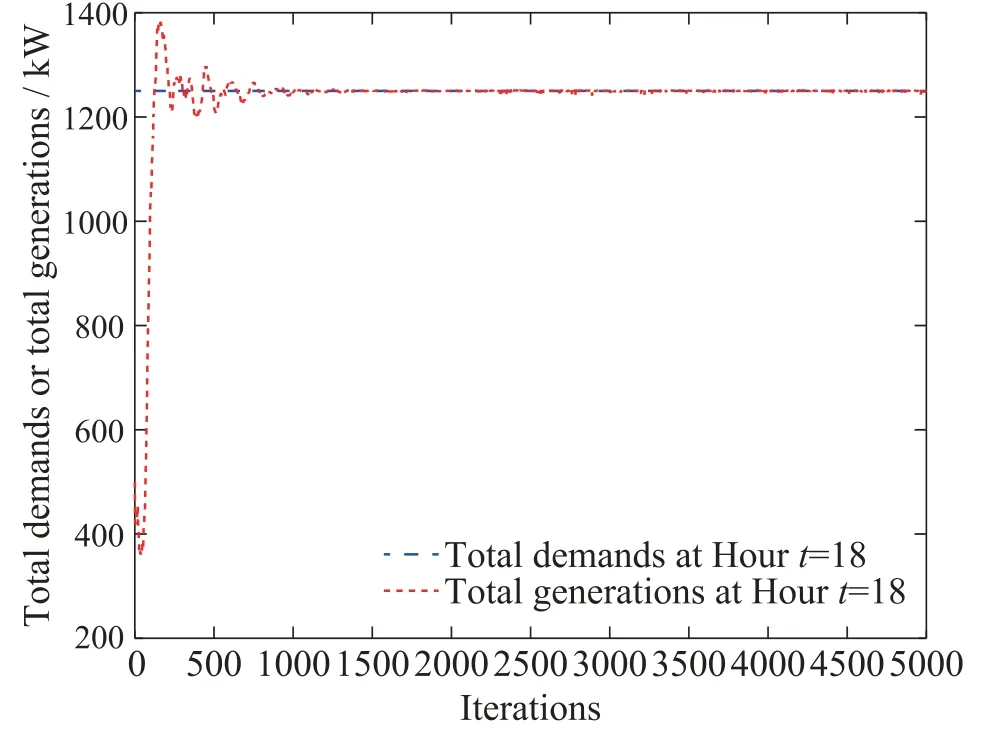
Fig.5 Total generations and total demands at hour 18

The evolution of dual variablesat hour 18 is given in Fig.8,from which we can obtain that all dual variables converge to-0.0883$/kWh.Fig.9 plots the residual iteration evolution of Alg.1 and Alg.2 in solving the DERs,respectively.The residual is expressed as(1/m)whereR24is the optimal power generated by DG or ES.It is shown that Alg.1 converges faster than Alg.2.

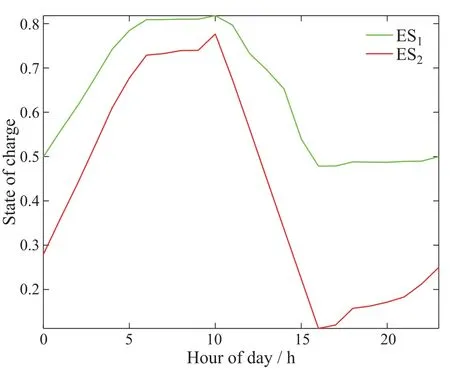
Fig.6 State of charge

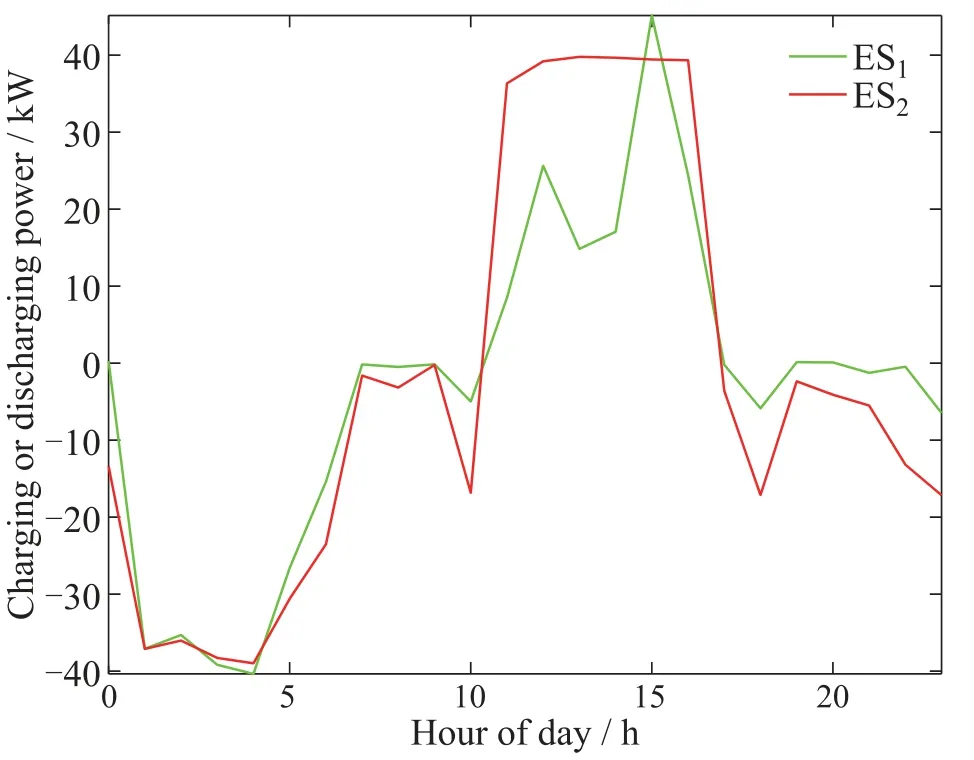
Fig.7 Charging and discharging power

Fig.8 Evolution of dual variables at hour 18

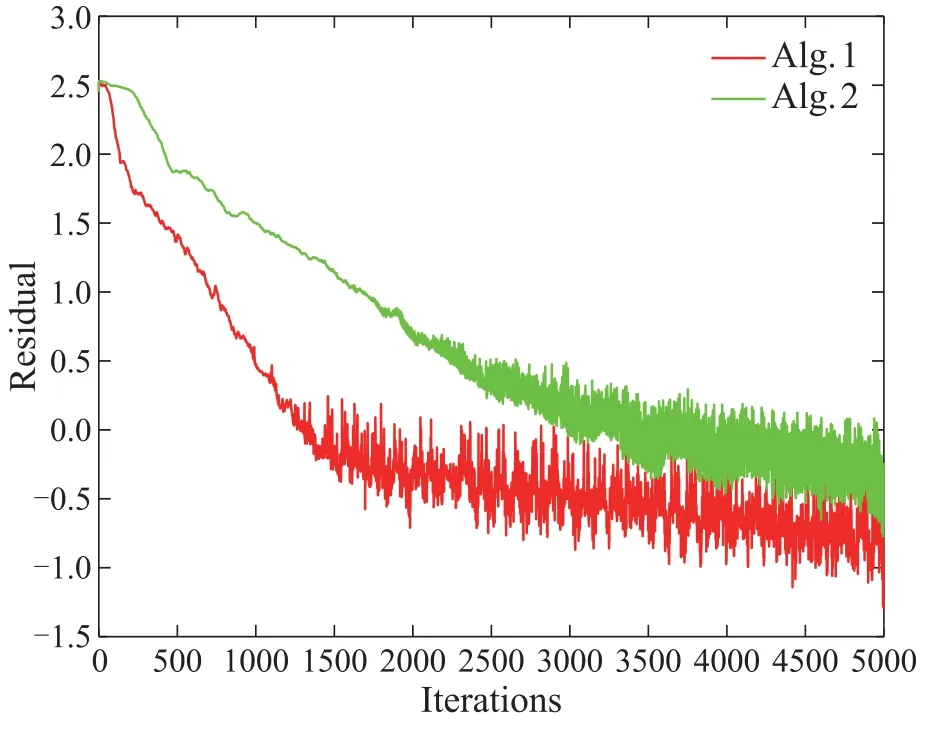
Fig.9 Performance comparison between Alg.1 and Alg.2

6 Conclusion

This paper has presented a distributed splitting algorithm for solving the optimal DERs coordination problem with both generation (storage) and environmental cost.The proposed algorithm enjoys certain flexibility due to the introduction of the relaxed factor and local step-sizes.Future work is to consider more practical physical constraints(such as the power flow capacities)and solve the considered problem over more complex scenarios,including time-varying or asynchronous networks,stochastic noises,etc.