Xun-Gao Wang(王勛高), Yuan Sun(孫遠), Liang Liu(劉亮), and Wu-Ming Liu(劉伍明)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Key Laboratory of Quantum Optics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

Three-dimensional type-II Weyl fermions possess overtilted cone-like low-energy band dispersion.Unlike the closed ellipsoidal Fermi surface for type-I Weyl fermions,the Fermi surface is an open hyperboloid for type-II Weyl fermions.We evaluate the spin and density susceptibility of type-II Weyl fermions with repulsive S-wave interaction by means of Green’s functions.We obtain the particle–hole continuum along the tilted momentum direction and perpendicular to the tilted momentum direction respectively.We find the zero sound mode in some repulsive interaction strengths by numerically solving the pole equations of the susceptibility within the random-phase approximation.

Keywords: Weyl fermions,zero sound mode,random-phase approximation

1.Introduction

Since the discover of topological insulator,[1,2]searching for novel topological states has been paid much attention.[3–6]Recently, some novel states, including Dirac semimetals[7–9]and Weyl semimetals,[10–14]have been confirmed in experiment.Weyl semimetal has emerged as novel topological states of matter, hosting low-energy excitations of massless Weyl fermions.Weyl fermions can be classified into type-I, which requires Lorentz invariance, and type-II Weyl fermions with broken Lorentz symmetry.[15,16]These two classes of Weyl fermions are characterized by the tilted parameter α, with α < 1 being type-I Weyl fermions, and α > 1 being type-II Weyl fermions in our Hamiltonian model Eq.(1).Unlike the closed ellipsoidal Fermi surface for type-I Weyl fermions,the Fermi surface is an open hyperboloid for type-II Weyl fermions, as shown in Fig.2, and the geometry of Fermi surface plays a crucial role in many material properties.Although Weyl nodes usually lie above the Fermi levelEF, we choose the type-II Weyl fermions system with Weyl nodes belowEF,[17,18]as illustrated in Fig.1.

The experimental realization of the type-II Weyl semimetal has been widely studied.[19–24]We have investigated the collective modes near the single Weyl node model with repulsive S-wave interaction for type-I Weyl fermions.[25]In order to lay the foundation for important applications of Weyl fermions to quantum simulation as well as information technologies in future, it is necessary to study the collective excitations for type-II Weyl fermions in ultracold atom gases.The superiority of ultracold atom gases than the semiconductor or semimetal is the tunable interaction strength by the technique of Feshbach resonance.[26,27]Collective excitations have received intensive studies.[28–31]In contrast to the partially tilted type-I Weyl fermions, whose lower band is full of particles and upper band is partially occupied, both the bands of the overtilted type-II Weyl fermions are partially occupied.In this paper we will focus on solving the poles equation of type-II Weyl fermions with repulsive S-wave interaction to obtain the collective modes within the random-phase approximation(RPA).

Our paper is organized as follow.In Section 2 we present the effective low-energy model for the type-II Weyl Fermi atomic gases with repulsive S-wave interaction in the continuum limit approximation.We show the energy dispersion of our model and the open hyperboloidal Fermi surface, which is the so-called double drumheadlike surfaces.We calculate the bare spin and density susceptibility by the Green’s functions theory and obtain collective modes by solving the poles equation of the susceptibility.The dispersion relations for the modes are shown by numerically solving the RPA equations in different interaction strengthes in Section 3.At last we will give the summation of our paper.

2.The model and calculation

We start from considering a low-energy effective model for a single Weyl node with repulsive S-wave interaction in three-dimensional fermionic system in the continuum limit approximation near the Weyl node.The effective Hamiltonian with the tilted term is given by

whereμ is the chemical potential where we consider only the Fermi surface above the Weyl node.α and β are the spin(pseudo-spin) indexes.Here and in the following, we treatas a system of units.The first termhis the noninteracting term of the Hamiltonian,whose eigenstates,the same as the eigenstates of the Weyl Hamiltonian without the tilted term,can be obtained as

where θ,φ are the polar angle and the azimuth angle in wave vector space,respectively.The energy eigenvalues are ξk,±=+v1kz?μ,which are shown in Fig.1.The second term in Eq.(1) represents the S-wave interaction in ultracold atomic gases.Here,we focus on the repulsive interaction case..The grey plane represents the Fermi level,which is above the Weyl node.

Fig.1.Band dispersion for type-II Weyl fermions in the k⊥–kz plane,where k⊥=

The Fermi surface of our model is not a closed curved surface because of the over-tilted term.We obtain that the Fermi surface is governed by the equation

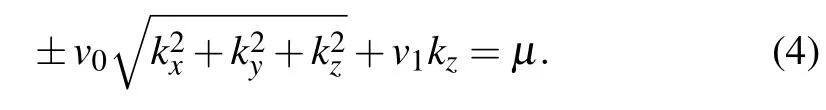
Finally,we obtain the standard conic section of Fermi surface

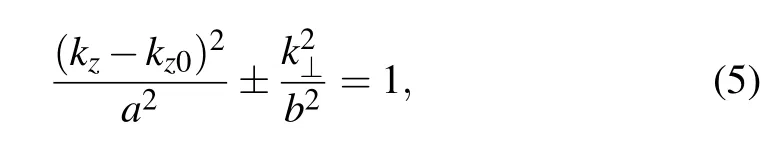
wherekz0=,the tilted parameter α =,a2=,b2=,andk0=,which corresponds to the Fermi momentum for type-I Weyl fermions without the tilted term.Here, ± correspond to ellipsoidal Fermi surface for α <1 and hyperboloidal Fermi surface for α >1,respectively.

It is interesting that the origin of coordinate is just a focus of a hyperboloid.Coincidentally,it is apparent that the origin of coordinate is also a focus of an ellipsoid for type-I Weyl fermions,

where ?represent the case of α <1 and α >1,respectively.Both the Fermi surfaces are depicted in Fig.2.

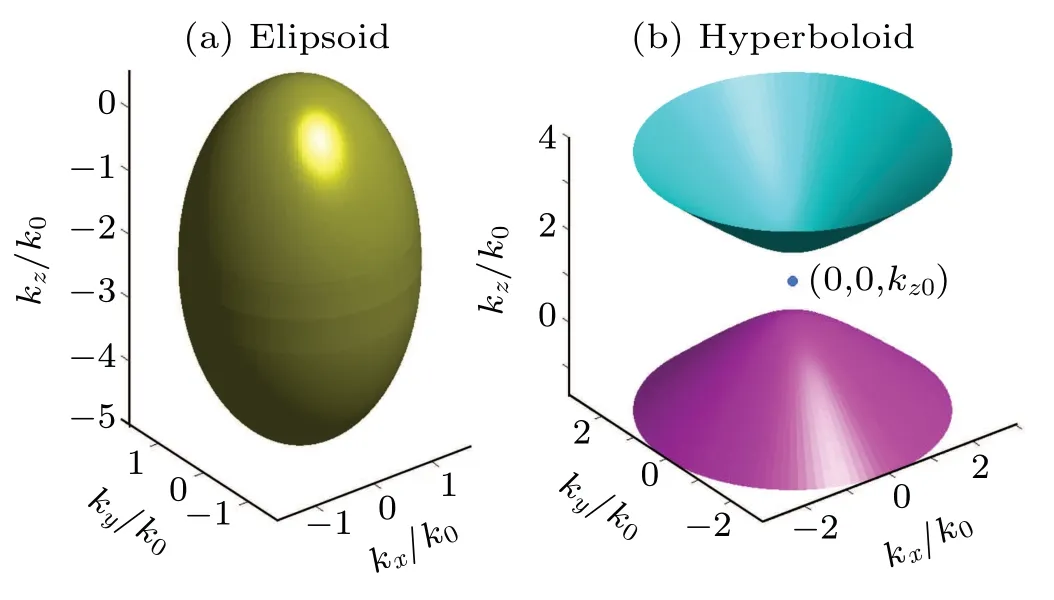
Fig.2.Schematic illustration of Fermi surface.(a) Schematic showing the ellipsoid Fermi surface for type-I Weyl fermions.(b)Schematic showing the hyperboloid Fermi surface for type-II Weyl fermions.The cyan branch of hyperboloid represents the Fermi surface of the lower band,and the other purple branch corresponds to the upper band.

In order to investigate the collective behavior in the system,we start from the spin and density susceptibility in Matsubara formalism,which can be written as

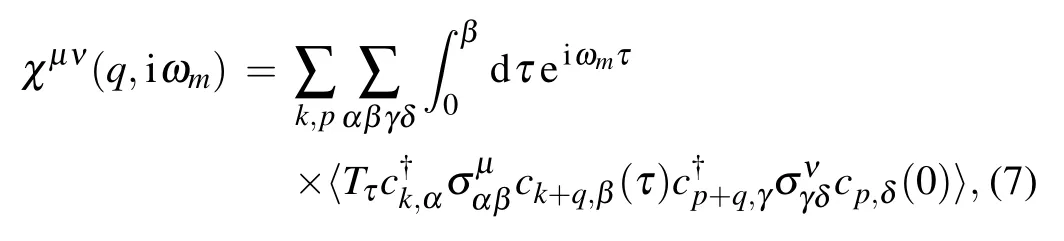
where σμ=(1,σz,σ+,σ?),and σ±=σx±iσyrepresent the raising and lowing operators.

By use of the Green’s function theory and the relationship between Matsubara Green’s function and the retarded Green’s function, the spin and density susceptibility without interaction can be written as

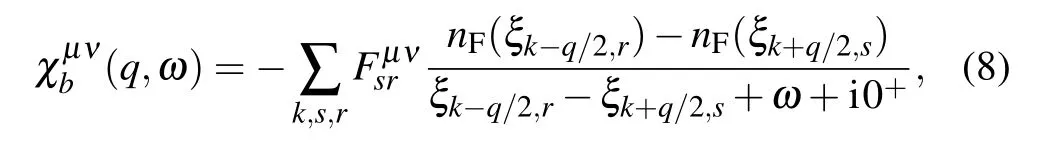
wherenF(ξ)is the Fermi distribution function andis an introduced overlap factor for calculation conveniently.At zero temperature,the distribution function is just the Heaviside step functionnF(ξ)=Θ(?ξ).The overlap factor,which contains two contributions from the intrasubband and the intersubband,has the form

wheres,rdenote the helicity indexes andPsis the projection operator with respect to the helicity eigenstates.

The ξk+q/2,s?ξk?q/2,rin the denominator of Eq.(8)represents the particle–hole excition energy,which consists of the contributions from the intrasubband and the intersubband.The particle–hole continuum,where the imaginary part of the susceptibility is nonzero, corresponding to the finite lifetime of collective modes, is shown in Fig.3 withqalong the tilted direction and in Fig.4 withqperpendicular to the tilted direction.

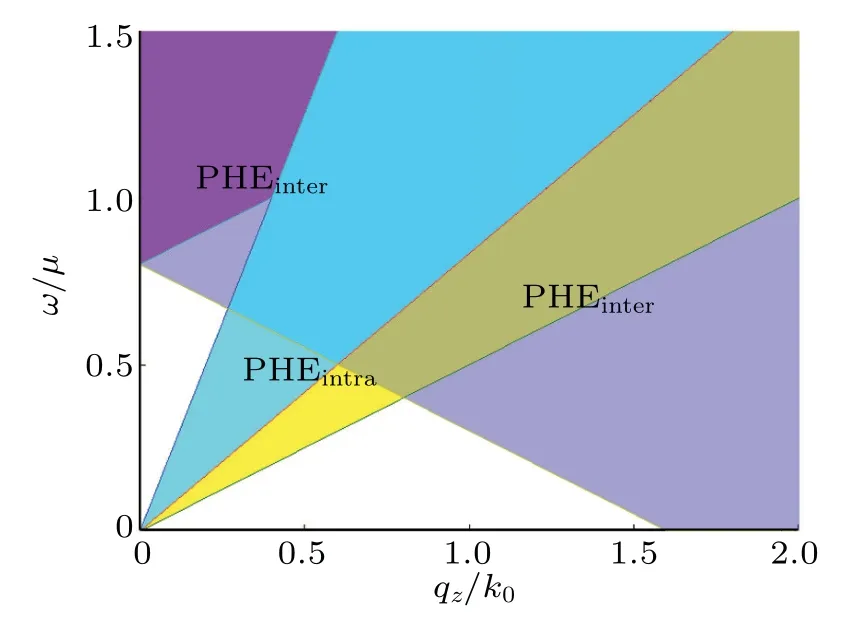
Fig.3.Particle–hole continuum with q along the tilted direction z-axis at the tilted parameter α =1.5.The purple and the light purple regions indicate the intersubband contribution to particle–hole excitations(PHEinter).The blue and the yellow regions indicate the intrasubband contribution to particle–hole excitations(PHEintra).

Fig.4.Particle–hole continuum with q perpendicular to the tilted direction z-axis at the tilted parameter α =1.5.Supposing q is along x-axis direction.The light red region indicates the intersubband contribution to particle–hole excitations (PHEinter).The blue and the green regions indicate the intrasubband contribution to particle–hole excitations(PHEintra).

We take advantage of the random-phase approximation to deal with the interaction term, and express the RPA susceptibility in terms of the bare susceptibility

where η =diag(1,?1,?1,?1).

3.Theoretical and numerical results

The open hyperboloid Fermi surface without the spherical symmetry for occupation of particles in the momentum space gives rise to a formidable integrand in the long-wavelength limit.Consequently, we focus on the collective behavior beyond the long-wavelength limit by numerical calculation.For the sack of simplicity, we only consider the case ofqalong the tilted direction.The detailed overlap factor has introduced in our previous article.[25]From the expression of the overlap factor, we can find that the 4×4 matrix can be written as four 2×2 block matrices, where all elements of the two off-diagonal 2×2 matrices have eφor e?φ.The integrals of these elements equal zero with respect to the momentum k as the azimuth angle φ runs from 0 to 2π.So the 4×4 matrix form of the spin and density susceptibility can be simplified into two uncoupled 2×2 submatrices.Then we can get two uncoupled poles equations of the spin and density susceptibility.Of course,the overlap factor does not have this symmetry with respect to the azimuth angle φ forqperpendicular to the tilted direction,and the 4×4 susceptibility cannot be grouped into two uncoupled 2×2 submatrices.

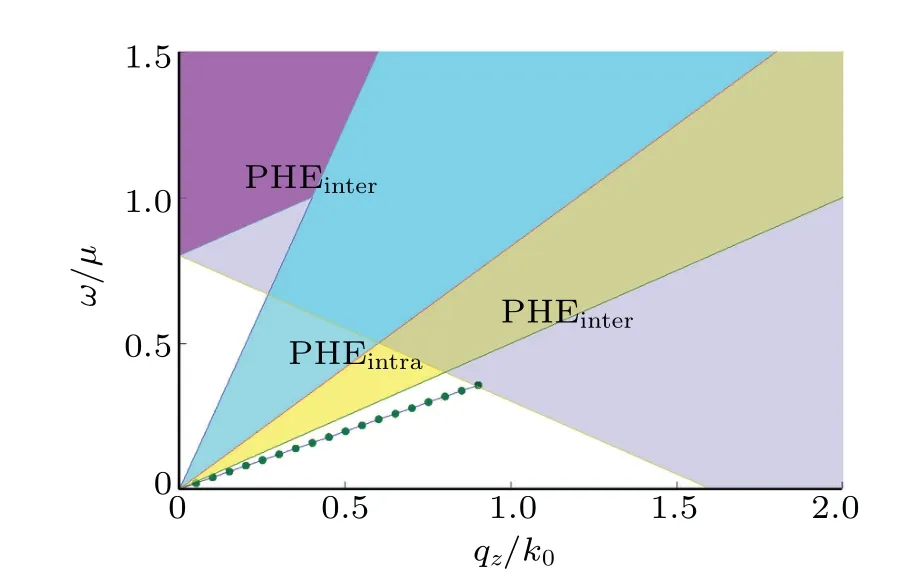
Fig.5.The collective zero sound mode at g=0.1.Here we take the tilted parameter α=1.5 and the ultraviolet cut-off momentum Λ=15k0 in numerical calculation.

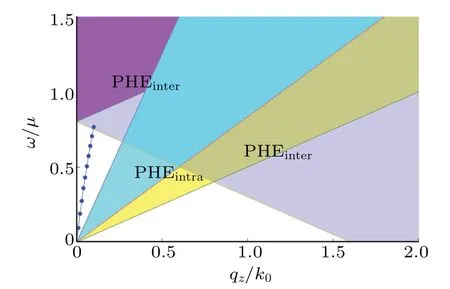
Fig.6.The collective zero sound mode at g=1.Here we take the tilted parameter α =1.5 and the ultraviolet cut-off momentum Λ =15k0 in numerical calculation.

We obtain the dispersion relations beyond the longwavelength limit by solving the poles equation using the numerical method.Because of the open hyperboloid Fermi surface for both bands, we define an unified ultraviolet cut-off momentum Λ for both bands, setting Λ =15k0in our calculations.We find that there is one zero sound mode atg=0.1,g=1 as well asg=5 for the tilted parameter α =1.5, as shown in Figs.5–7,respectively.Here,the interaction strength parameterghas the energy dimension,and we makegin units of chemical potentialμ for calculations.We find that the collective modes fall into the particle–hole continuum at some interaction strengths,such asg=0.2 andg=0.5.

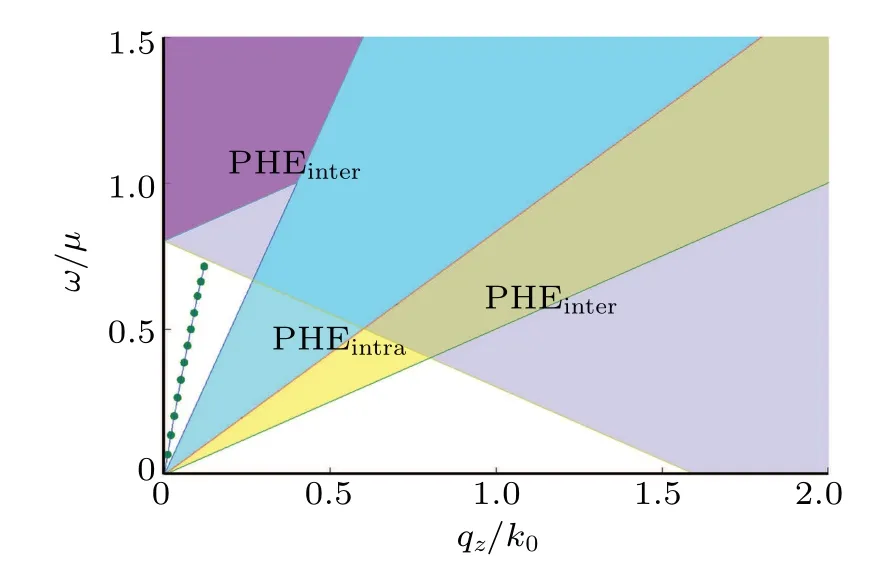
Fig.7.The collective zero sound mode at g=5.Here we take the tilted parameter α =1.5 and the ultraviolet cut-off momentum Λ =15k0 in numerical calculation.

4.Conclusion

We evaluate the collective modes in three-dimensional fermion system governed by type-II Weyl Hamiltonian with repulsive S-wave interaction.In contrast to the fixed Coulomb interaction in condensed matter,we can find collective modes depending on the interaction strength in ultracold atomic gases,which can be tuned into a large range of values by Feshbach resonance in ultracold atoms.By contrast,there exist one zero sound mode,one gapped mode or two gapped modes for different repulsive interaction strengthes for the type-I Weyl fermions without the tilted term, and we find that only one zero sound mode appears for some interaction strength, such asg=0.1,g=1 andg=5.

Acknowledgements

Project supported by the National Key R&D Program of China (Grant No.2016YFA0301500), the National Natural Science Foundation of China(Grants No.61835013),and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant Nos.XDB01020300 and XDB21030300).We are grateful to Sun FaDi for useful discussions.